排序六部曲之（三）堆排序

堆排序的要点在于构建一个最大推或者最小堆。那么什么是最大堆、最小堆呢？

一、概念介绍

二叉堆：二叉堆是一棵完全二叉树

二叉堆的性质：

1、二叉堆的父节点的值总是大于或者等于（小于或者等于）子节点的值

2、当父节点的值大于或者等于子节点的值时为最大堆，当父节点的值小于或者等于子节点时最小堆

3、通常对于给定的结点i可以根据在数组中的位置求出其父节点的位置、左右子节点的位置，对于下标从0开始的数组，位置为i的结点的父节点的位置为(i-1)/2，左子节点的位置为2*i+1，右子节点的位置为2*i+2

4、没有子节点的结点为子叶结点，有一个或者两个子节点的结点为非子叶结点，对于下标从0开始长度为n序列，非子叶结点的下标为：0~n/2-1，子叶结点的下标为：n/2~n-1

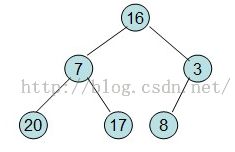
序列16 7 3 20 17 8对应的二叉堆如下图所示：（图是盗的）

二、如何把一个无序的二叉堆变换成最大堆呢？（本文全部采用最大堆）

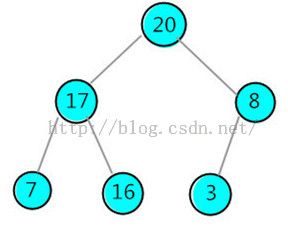
        从最后一个非子叶节点开始一直到根节点依次对每个结点进行调整，调整方式为：该结点与其子节中键值较大的一个比较交换（若该结点的值小于该较大的子节点的值则交换位置），对被交换位置的子节点进行调整，若没有交换则不需调整。过程演示如下图

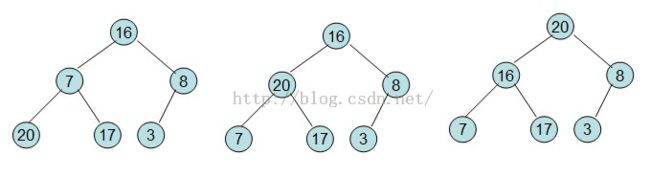
20和16交换后导致16不满足最大堆的性质，需要对16进行调整

下标从0开始长度为len的序列最大堆

	//onlyRoot:是否只对根节点进行调整
	static void minHeap(int[] a,int len,boolean onlyRoot)
	{
		//s~d为非子叶结点的下标
		int s;
		if(onlyRoot)
		{
			s=0;
		}else 
		{
			s=len/2-1;
		}
		int d=0;
		for(int i=s;i>=d;i--)
		{
			int k=i;
			for(int j=2*k+1;j<len;k=j,j=2*k+1)
			{
				if(j+1<len && a[j+1]>a[j])
				{
					j=j+1;
				}
				if(a[k]<a[j])
				{
					swap(k, j);//交换a[k],a[j]
				}else
				{
					break;
				}
			}
		}
	}

三、如何利用最大推给序列排序呢？

由上面对最大堆的分析可知，最大堆的根节点的值总是最大的，根据这个性质，我们只需要交换第最大堆的第一个位置与最后一个位置并将序列的长度减1，然后在求剩下的序列的最大堆。注意：除了第一次求最大堆需要对每个非子叶结点进行调整外，以后的每次都只需要对根节点进行调整，因为交换操作只是使得根节点不满足最大堆的性质，对其余的非子叶结点没有影响。

求序列的最大堆，这个过程已经在上面演示过了，这里直接拿来用

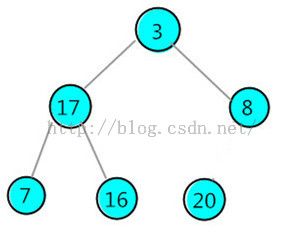
交换根节点20与最后一个节点3的位置

交换使得根节点3不满足最大堆的性质，对根节点3进行调整

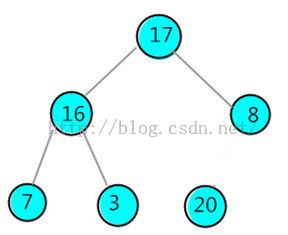
交换根节点17余最后一个节点3的位置

调整根节点——>交换根节点与最后一个节点的位置，持续这个过程直到堆中只剩下一个节点

	static void sortDown()
	{
		minHeap(a, n,false);
		swap(0, n-1);
		for(int len=n-1;len>1;len--)
		{
			minHeap(a, len,true);
			swap(0, len-1);
		}
	}