数据挖掘2关于fp-tree
FP-Tree算法
FPTree算法:在不生成候选项的情况下,完成Apriori算法的功能。
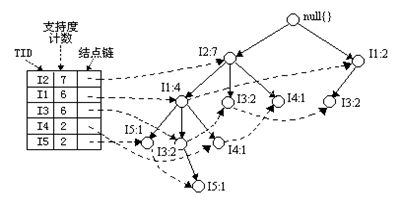
FPTree算法的基本数据结构,包含一个一棵FP树和一个项头表,每个项通过一个结点链指向它在树中出现的位置。基本结构如下所示。需要注意的是项头表需要按照支持度递减排序,在FPTree中高支持度的节点只能是低支持度节点的祖先节点。
另外还要交代一下FPTree算法中几个基本的概念:
FP-Tree:就是上面的那棵树,是把事务数据表中的各个事务数据项按照支持度排序后,把每个事务中的数据项按降序依次插入到一棵以NULL为根结点的树中,同时在每个结点处记录该结点出现的支持度。
条件模式基:包含FP-Tree中与后缀模式一起出现的前缀路径的集合。也就是同一个频繁项在PF树中的所有节点的祖先路径的集合。比如I3在FP树中一共出现了3次,其祖先路径分别是{I2,I1:2(频度为2)},{I2:2}和{I1:2}。这3个祖先路径的集合就是频繁项I3的条件模式基。
条件树:将条件模式基按照FP-Tree的构造原则形成的一个新的FP-Tree。比如上图中I3的条件树就是:
1、 构造项头表:扫描数据库一遍,得到频繁项的集合F和每个频繁项的支持度。把F按支持度递降排序,记为L。
2、 构造原始FPTree:把数据库中每个事物的频繁项按照L中的顺序进行重排。并按照重排之后的顺序把每个事物的每个频繁项插入以null为根的FPTree中。如果插入时频繁项节点已经存在了,则把该频繁项节点支持度加1;如果该节点不存在,则创建支持度为1的节点,并把该节点链接到项头表中。
3、 调用FP-growth(Tree,null)开始进行挖掘。伪代码如下:
procedure FP_growth(Tree, a)
if Tree 含单个路径P then{
for 路径P中结点的每个组合(记作b)
产生模式b U a,其支持度support = b 中结点的最小支持度;
} else {
for each a i 在Tree的头部(按照支持度由低到高顺序进行扫描){
产生一个模式b = a i U a,其支持度support = a i .support;
构造b的条件模式基,然后构造b的条件FP-树Treeb;
if Treeb 不为空 then
调用 FP_growth (Treeb, b);
}
}
FP-growth是整个算法的核心,再多啰嗦几句。
FP-growth函数的输入:tree是指原始的FPTree或者是某个模式的条件FPTree,a是指模式的后缀(在第一次调用时a=NULL,在之后的递归调用中a是模式后缀)
FP-growth函数的输出:在递归调用过程中输出所有的模式及其支持度(比如{I1,I2,I3}的支持度为2)。每一次调用FP_growth输出结果的模式中一定包含FP_growth函数输入的模式后缀。
我们来模拟一下FP-growth的执行过程。
1、 在FP-growth递归调用的第一层,模式前后a=NULL,得到的其实就是频繁1-项集。
2、 对每一个频繁1-项,进行递归调用FP-growth()获得多元频繁项集。
下面举两个例子说明FP-growth的执行过程。
1、I5的条件模式基是(I2 I1:1), (I2 I1 I3:1),I5构造得到的条件FP-树如下。然后递归调用FP-growth,模式后缀为I5。这个条件FP-树是单路径的,在FP_growth中直接列举{I2:2,I1:2,I3:1}的所有组合,之后和模式后缀I5取并集得到支持度>2的所有模式:{ I2 I5:2, I1 I5:2, I2 I1 I5:2}。
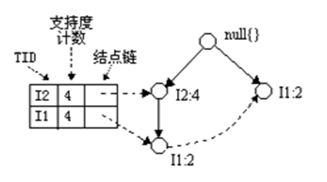
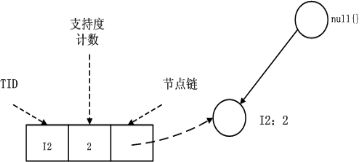
2、I5的情况是比较简单的,因为I5对应的条件FP-树是单路径的,我们再来看一下稍微复杂一点的情况I3。I3的条件模式基是(I2 I1:2), (I2:2), (I1:2),生成的条件FP-树如左下图,然后递归调用FP-growth,模式前缀为I3。I3的条件FP-树仍然是一个多路径树,首先把模式后缀I3和条件FP-树中的项头表中的每一项取并集,得到一组模式{I2 I3:4, I1 I3:4},但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth,模式后缀为{I1,I3},{I1,I3}的条件模式基为{I2:2},其生成的条件FP-树如右下图所示。这是一个单路径的条件FP-树,在FP_growth中把I2和模式后缀{I1,I3}取并得到模式{I1 I2 I3:2}。理论上还应该计算一下模式后缀为{I2,I3}的模式集,但是{I2,I3}的条件模式基为空,递归调用结束。最终模式后缀I3的支持度>2的所有模式为:{ I2 I3:4, I1 I3:4, I1 I2 I3:2}
| item |
条件模式基 |
条件FP-树 |
产生的频繁模式 |
| I5 I4 I3 I1 |
{(I2 I1:1),(I2 I1 I3:1) {(I2 I1:1), (I2:1)} {(I2 I1:2), (I2:2), (I1:2)} {(I2:4)} |
<I2:2, I1:2> <I2:2> <I2:4, I1:2>, <I1:2> <I2:4> |
I2 I5:2, I1 I5:2, I2 I1 I5:2 I2 I4:2 I2 I3:4, I1 I3:4, I2 I1 I3:2 I2 I1:4 |
FP-growth算法比Apriori算法快一个数量级,在空间复杂度方面也比Apriori也有数量级级别的优化。但是对于海量数据,FP-growth的时空复杂度仍然很高,可以采用的改进方法包括数据库划分,数据采样等等。
==============================
顺便说一下:关于如何列出所有组合的方法。
最简单粗暴的方法就是递归呀,简单还容易理解。不过后来我想还可以这样做。对于n个数,1..2..3.....n,我们对于一个数有两种态度,比如取就是0,不取就是1,那么我用一长串的的01表示,那我们就用这样的方法不断加1,当然二进制哈,不断加1,直到最大,然后把这个数字对应到数字上的取与不取就行了。
来源:http://blog.csdn.net/sealyao/article/details/6460578