B-树的插入、查找、删除 及 可执行的C语言代码
前面讨论的查找都是内查询算法,被查询的数据都在内存。当查询的数据放在外存,用平衡二叉树作磁盘文件的索引组织时,若以结点为内外存交换的单位,则找到需要的关键字之前,平均要进行lgn次磁盘读操作,而磁盘、光盘的读写时间要比随机存取的内存代价大得多。其二,外存的存取是以“页”为单位的,一页的大小通常是1024字节或2048字节。
针对上述特点,1972年R.Bayer和E.M.Cright提出了一种B-树的多路平衡查找树,以适合磁盘等直接存取设备上组织动态查找表。B-树上算法的执行时间主要由读、写磁盘的次数来决定,故一次I/O操作应读写尽可能多的信息。因此B-树的结点规模一般以一个磁盘页为单位。一个结点包含的关键字及其孩子个数取决于磁盘页的大小。
一、基本概念
B-树又称为多路平衡查找树。
一棵度为m的B-树称为m阶B_树。一个结点有k个孩子时,必有k-1个关键字才能将子树中所有关键字划分为k个子集。B-树中所有结点的孩子结点最大值称为B-树的阶,通常用m表示。从查找效率考虑,一般要求m≥3。一棵m阶的B-树或者是一棵空树,或者是满足下列要求的m叉树:
(1)根结点或者为叶子,或者至少有两棵子树,至多有m棵子树。
(2)除根结点外,所有非终端结点至少有ceil(m/2)棵子树,至多有m棵子树。
(3)所有叶子结点都在树的同一层上。
(4)每个结点的结构为:
(n,A0,K1,A1,K2,A2,… ,Kn,An)
其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。
Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。An所指子树中所有结点的关键字均大于Kn。
n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
比如,一棵3阶B-树,m=3。它满足:
(1)每个结点的孩子个数小于等于3。
(2)除根结点外,其他结点至少有=2个孩子。
(3)根结点有两个孩子结点。
(4)除根结点外的所有结点的n大于等于=1,小于等于2。
二、B-树查找的算法思想
1、B-树的查找
B-树的查找过程:根据给定值查找结点和在结点的关键字中进行查找交叉进行。首先从根结点开始重复如下过程:
若比结点的第一个关键字小,则查找在该结点第一个指针指向的结点进行;若等于结点中某个关键字,则查找成功;若在两个关键字之间,则查找在它们之间的指针指向的结点进行;若比该结点所有关键字大,则查找在该结点最后一个指针指向的结点进行;若查找已经到达某个叶结点,则说明给定值对应的数据记录不存在,查找失败。
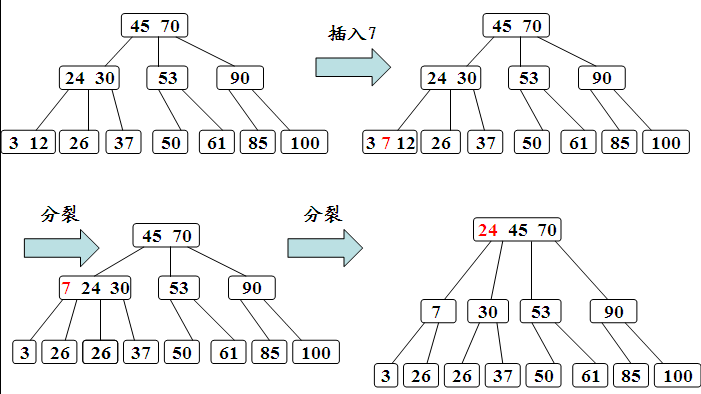
2. B-树的插入
插入的过程分两步完成:
(1)利用前述的B-树的查找算法查找关键字的插入位置。若找到,则说明该关键字已经存在,直接返回。否则查找操作必失败于某个最低层的非终端结点上。
(2)判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足,则说明该结点还有空位置,直接把关键字k插入到该结点的合适位置上。若不满足,说明该结点己没有空位置,需要把结点分裂成两个。
分裂的方法是:生成一新结点。把原结点上的关键字和k按升序排序后,从中间位置把关键字(不包括中间位置的关键字)分成两部分。左部分所含关键字放在旧结点中,右部分所含关键字放在新结点中,中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过(m-1),则要再分裂,再往上插。直至这个过程传到根结点为止。


3、B-树的删除
在B-树上删除关键字k的过程分两步完成:
(1)利用前述的B-树的查找算法找出该关键字所在的结点。然后根据 k所在结点是否为叶子结点有不同的处理方法。
(2)若该结点为非叶结点,且被删关键字为该结点中第i个关键字key[i],则可从指针son[i]所指的子树中找出最小关键字Y,代替key[i]的位置,然后在叶结点中删去Y。
因此,把在非叶结点删除关键字k的问题就变成了删除叶子结点中的关键字的问题了。
在B-树叶结点上删除一个关键字的方法是
首先将要删除的关键字 k直接从该叶子结点中删除。然后根据不同情况分别作相应的处理,共有三种可能情况:
(1)如果被删关键字所在结点的原关键字个数n>=ceil(m/2),说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单,只需从该结点中直接删去关键字即可。
(2)如果被删关键字所在结点的关键字个数n等于ceil(m/2)-1,说明删去该关键字后该结点将不满足B-树的定义,需要调整。
调整过程为:如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右(左)兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右(左)兄弟结点中最小(大)关键字上移至双亲结点。而将双亲结点中小(大)于该上移关键字的关键字下移至被删关键字所在结点中。
(3)如果左右兄弟结点中没有“多余”的关键字,即与该结点相邻的右(左)兄弟结点中的关键字数目均等于ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左(或右)兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后,该结点中剩余的关键字加指针,加上双亲结点中的关键字Ki一起,合并到Ai(是双亲结点指向该删除关键字结点的左(右)兄弟结点的指针)所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于ceil(m/2)-1,则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。
总之,设所删关键字为非终端结点中的Ki,则可以指针Ai所指子树中的最小关键字Y代替Ki,然后在相应结点中删除Y。对任意关键字的删除都可以转化为对最下层关键字的删除。

如图示:
a、被删关键字Ki所在结点的关键字数目不小于ceil(m/2),则只需从结点中删除Ki和相应指针Ai,树的其它部分不变。

b、被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1,则需调整。调整过程如上面所述。

c、被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1,假设该结点有右兄弟,且其右兄弟结点地址由其双亲结点指针Ai所指。则在删除关键字之后,它所在结点的剩余关键字和指针,加上双亲结点中的关键字Ki一起,合并到Ai所指兄弟结点中(若无右兄弟,则合并到左兄弟结点中)。如果因此使双亲结点中的关键字数目少于ceil(m/2)-1,则依次类推。

三、B-树的C语言描述
1、存储结构

2、插入

3、查找

四、B-树的C语言实现
#include "stdio.h"#include "stdlib.h"
#include "math.h"
#define OK 1
#define ERROR -1
#define m 3 //3阶树
#define N 16 //数据元素个数
#define MAX 5 //字符串最大长度+1
typedef int KeyType;
struct Others //记录的其它部分
{
char info[MAX];
};
struct Record
{
KeyType key; //关键字
Others others; //其它部分
};
typedef struct BTNode
{
int keynum; //结点中关键字个数
BTNode *parent;//指向双亲节点
struct Node //结点向量类型
{
KeyType key; //关键字向量
BTNode *ptr;//子树指针向量
Record *recptr; //记录向量指针
}node[m+1]; //key,recptr的0号单元未用
}BTNode,*BTree;
struct Result //B树的查找结果类型
{
BTNode *pt; //指向找到的结点
int i; //在节点中关键字序号,1...m
int tag; //1表示查找成功,0表示查找失败。
};
int InitDSTable(BTree &DT)
{
DT=NULL;
return OK;
}//InitDSTable
void DestroyDSTable(BTree &DT)
{
int i;
if(DT) //非空树
{
for(i=0;i<=DT->keynum;i++)
DestroyDSTable(DT->node[i].ptr);
free(DT);
DT=NULL;
}//if
}//DestroyDSTable
int Search(BTree p,KeyType K)
{//在p->node[1...keytype].key中查找i,使得p->node[i].key<=K<
//p->node[i+1].key
int i=0,j;
for(j=1;j<=p->keynum;j++)
if(p->node[j].key<=K)
i=j;
return i;
}//Search
void Insert(BTree &q,int i,Record *r,BTree ap)
{//将r->key、r和ap分别插入到q->key[i+1]、
//q->recptr[ i+1]和q->ptr[i+1]中
int j;
for(j=q->keynum;j>i;j--) //空出q->node[i+1]
q->node[j+1]=q->node[j];
q->node[i+1].key=r->key;
q->node[i+1].ptr=ap; //前加入的结点,还没有儿子结点
q->node[i+1].recptr=r;
q->keynum++;
}//Insert
void NewRoot(BTree &T,Record *r,BTree ap)
{// 生成含信息(T,r,ap)的新的根结点*T,原T和ap为子树指针
BTree p;
p=(BTree)malloc(sizeof(BTNode));
p->node[0].ptr=T;
T=p;
if(T->node[0].ptr)
T->node[0].ptr->parent=T;
T->parent=NULL;
T->keynum=1;
T->node[1].key=r->key;
T->node[1].recptr=r;
T->node[1].ptr=ap;
if(T->node[1].ptr)
T->node[1].ptr->parent=T;
}//NewRoot
void split(BTree &q,BTree &ap)
{// 将结点q分裂成两个结点,前一半保留,后一半移入新生结点ap
int i,s=(m+1)/2;
ap=(BTree)malloc(sizeof(BTNode));//生成新结点ap
ap->node[0].ptr=q->node[s].ptr;//原来结点中间位置关键字相应指针指向的子树放到
//新生成结点的0棵子树中去
for(i=s+1;i<=m;i++) //后一半移入ap
{
ap->node[i-s]=q->node[i];
if(ap->node[i-s].ptr)
ap->node[i-s].ptr->parent=ap;
}//for
ap->keynum=m-s;
ap->parent=q->parent;
q->keynum=s-1; // q的前一半保留,修改keynum
}//split
void InsertBTree(BTree &T,Record *r,BTree q,int i)
{//在m阶B树T上结点*q的key[i]与key[i+1]之间插入关键字K的指针r。若引起
// 结点过大,则沿双亲链进行必要的结点分裂调整,使T仍是m阶B树。
BTree ap=NULL;
int finished=false;
int s;
Record *rx;
rx=r;
while(q&&!finished)
{
Insert(q,i,rx,ap);//将r->key、r和ap分别插入到q->key[i+1]、
//q->recptr[i+1]和q->ptr[i+1]中
if(q->keynum<m)
finished=true;
else
{//分裂结点*q
s=(m+1)/2;
rx=q->node[s].recptr;
split(q,ap);//将q->key[s+1..m],q->ptr[s..m]和q->recptr[s+1..m]
//移入新结点*ap
q=q->parent;
if(q)
i=Search(q,rx->key);//在双亲结点*q中查找rx->key的插入位置
}//else
}//while
if(!finished) //T是空树(参数q初值为NULL)或根结点已分裂为
//结点*q和*ap
NewRoot(T,rx,ap);
}//InsertBTree
Result SearchBTree(BTree T,KeyType K)
{// 在m阶B树T上查找关键字K,返回结果(pt,i,tag)。若查找成功,则特征值
// tag=1,指针pt所指结点中第i个关键字等于K;否则特征值tag=0,等于K的
// 关键字应插入在指针Pt所指结点中第i和第i+1个关键字之间。
BTree p=T,q=NULL; //初始化,p指向待查结点,q指向p的双亲
int found=false;
int i=0;
Result r;
while(p&&!found)
{
i=Search(p,K);//p->node[i].key≤K<p->node[i+1].key
if(i>0&&p->node[i].key==K)
found=true;
else
{
q=p;
p=p->node[i].ptr;//在子树中继续查找
}//else
}//while
r.i=i;
if(found)
{
r.pt=p;
r.tag=1;
}//if
else
{
r.pt=q;
r.tag=0;
}//else
return r;
}//SearchBTree
void print(BTNode c,int i) // TraverseDSTable()调用的函数
{
printf("(%d,%s)",c.node[i].key,c.node[i].recptr->others.info);
void TraverseDSTable(BTree DT,void(*Visit)(BTNode,int))
{// 初始条件: 动态查找表DT存在,Visit是对结点操作的应用函数
// 操作结果: 按关键字的顺序对DT的每个结点调用函数Visit()一次且至多一次
int i;
if(DT) //非空树
{
if(DT->node[0].ptr) // 有第0棵子树
TraverseDSTable(DT->node[0].ptr,Visit);
for(i=1;i<=DT->keynum;i++)
{
Visit(*DT,i);
if(DT->node[i].ptr) // 有第i棵子树
TraverseDSTable(DT->node[i].ptr,Visit);
}//for
}//if
}//TraverseDSTable
void InputBR(BTree &t,Record r[])
{
Result s;
for(int i=0;i<N;i++)
{
s=SearchBTree(t,r[i].key);
if(!s.tag)
InsertBTree(t,&r[i],s.pt,s.i);
}
}//InputBR
void UserSearch(BTree t)
{
int i;
Result s;
printf("\n请输入待查找记录的关键字: ");
scanf("%d",&i);
s=SearchBTree(t,i);
if(s.tag)
print(*(s.pt),s.i);
else
printf("没找到");
printf("\n");
}//UserSearch
void DeleteIt(BTree t,BTNode *dnode,int id)
{
if(dnode->keynum>=ceil(m/2))
{
dnode->keynum--;
dnode->node[id].ptr=NULL;
}//if被删关键字Ki所在结点的关键字数目不小于ceil(m/2),则只需从结点中删除Ki和相应指针Ai,树的其它部分不变。
else if((dnode->keynum==(ceil(m/2)-1))&&((id+1)<(m-1))&&dnode->parent->node[id+1].ptr->keynum>(ceil(m/2)-1))
{
for(int i=1;i<m&&dnode->parent->node[i].key < dnode->parent->node[id+1].ptr->node[1].key;i++)
dnode->node[i].key=dnode->parent->node[i].key;
dnode->parent->node[1].key=dnode->parent->node[id+1].ptr->node[1].key;
(dnode->parent->node[id+1].ptr->keynum)--;
}//else if 被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1,则需调整。本次为与右兄弟调整
else if((dnode->keynum==(ceil(m/2)-1))&&((id-1)>0 )&&dnode->parent->node[id-1].ptr->keynum>(ceil(m/2)-1))
{
for(int i=1;i<m&&dnode->parent->node[i].key > dnode->parent->node[id-1].ptr->node[dnode->parent->node[id-1].ptr->keynum].key;i++)
dnode->node[i].key=dnode->parent->node[i].key;
dnode->parent->node[1].key=dnode->parent->node[id-1].ptr->node[dnode->parent->node[id-1].ptr->keynum].key;
(dnode->parent->node[id-1].ptr->keynum)--;
}//2-else if被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1,则需调整。本次为与左兄弟调整
else if((dnode->keynum==(ceil(m/2)-1))&&((id+1)<(m-1))&&dnode->parent->node[id+1].ptr->keynum==(ceil(m/2)-1))
{
do
{
BTree tmp;
tmp=dnode;
dnode->parent->node[id+1].ptr->node[2]=dnode->parent->node[id+1].ptr->node[1];
dnode->parent->node[id+1].ptr->node[1]=dnode->parent->node[1];
dnode->parent->node[id+1].ptr->keynum++;
dnode->parent->node[id+1].ptr->node[0].ptr=dnode->node[1].ptr;
dnode->parent->keynum--;
dnode->parent->node[id].ptr=NULL;
tmp=dnode;
if(dnode->parent->keynum>=(ceil(m/2)-1))
dnode->parent->node[1]=dnode->parent->node[2];
dnode=dnode->parent;
free(tmp);
}while(dnode->keynum<(ceil(m/2)-1)); //双亲中keynum<
}//3-else if被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1,本次假设右兄弟存在
else if((dnode->keynum==(ceil(m/2)-1))&&(id-1)>0 &&dnode->parent->node[id-1].ptr->keynum==(ceil(m/2)-1))
{
do
{
BTree tmp;
tmp=dnode;
dnode->parent->node[id-1].ptr->node[2]=dnode->parent->node[id-1].ptr->node[1];
dnode->parent->node[id-1].ptr->node[1]=dnode->parent->node[1];
dnode->parent->node[id-1].ptr->keynum++;
dnode->parent->node[id-1].ptr->node[0].ptr=dnode->node[1].ptr;
dnode->parent->keynum--;
dnode->parent->node[id].ptr=NULL;
tmp=dnode;
if(dnode->parent->keynum>=(ceil(m/2)-1))
dnode->parent->node[1]=dnode->parent->node[2];
dnode=dnode->parent;
free(tmp);
}while(dnode->keynum<(ceil(m/2)-1)); //双亲中keynum<
}//4-else if被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1,本次假设左兄弟存在
else printf("Error!"); //出现异常
}//DeleteIt
void UserDelete(BTree t)
{
KeyType date;
Result s;
printf("Please input the date you want to delete:\n");
scanf("%d",&date);
s=SearchBTree(t,date);
if(!s.tag) printf("Search failed,no such date\n");
else DeleteIt(t,s.pt,s.i);
}//UserDelete
int main()
{
Record r[N]={{24,"1"},{45,"2"},{53,"3"},{12,"4"},{37,"5"},
{50,"6"},{61,"7"},{90,"8"},{100,"9"},{70,"10"},
{3,"11"},{30,"12"},{26,"13"},{85,"14"},{3,"15"},
{7,"16"}};
BTree t;
InitDSTable(t);
InputBR(t,r);
printf("按关键字的顺序遍历B_树:\n");
TraverseDSTable(t,print);
UserSearch(t);
UserDelete(t);
TraverseDSTable(t,print);
DestroyDSTable(t);
return 1;
}
五、复杂度分析
B-树查找包含两种基本动作:
●在B-树上查找结点
●在结点中找关键字
前一操作在磁盘上进行,后一操作在内存进行。因此查找效率主要由前一操作决定。在磁盘上查找的次数取决于关键字结点在B-树上的层次数。
定理:若n≥1,m≥3,则对任意一棵具有n个关键字的m阶B-树,其树高度h至多为logt((n+1)/2)+1,t= ceil(m/2)。也就是说根结点到关键字所在结点的路径上涉及的结点数不超过logt((n+1)/2)+1。推理如下:
另一套代码,可执行,附带时间测试函数。
/* btrees.h */
/*
* 平衡多路树的一种重要方案。
* 在 1970 年由 R. Bayer 和 E. McCreight 发明。
*/
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <assert.h>
#include <windows.h>
#define M 1
/* B 树的阶,即非根节点中键的最小数目。
* 有些人把阶定义为非根节点中子树的最大数目。
*/
typedef int typekey;
typedef struct btnode { /* B-Tree 节点 */
int d; /* 节点中键的数目 */
typekey k[M+2]; /* 键 */
char *v[M+2]; /* 值 */
struct btnode *p[M+2+1]; /* 指向子树的指针 */
} node, *btree;
/*
* 每个键的左子树中的所有的键都小于这个键,
* 每个键的右子树中的所有的键都大于等于这个键。
* 叶子节点中的每个键都没有子树。
*/
/* 当 M 等于 1 时也称为 2-3 树
* +----+----+
* | k0 | k1 |
* +-+----+----+---
* | p0 | p1 | p2 |
* +----+----+----+
*/
//extern int btree_disp; /* 查找时找到的键在节点中的位置 */
//extern char * InsValue; /* 与要插的键相对应的值 */
int btree_disp; /* 查找时找到的键在节点中的位置 */
char * InsValue; /* 与要插的键相对应的值 */
int flag; /* 节点增减标志 */
int btree_level; /* 多路树的高度 */
int btree_count; /* 多路树的键总数 */
int node_sum; /* 多路树的节点总数 */
int level; /* 当前访问的节点所处的高度 */
btree NewTree; /* 在节点分割的时候指向新建的节点 */
typekey InsKey; /* 要插入的键 */
btree search(typekey, btree);
btree insert(typekey,btree);
btree delete(typekey,btree);
int height(btree);
int count(btree);
double payload(btree);
btree deltree(btree);
static void InternalInsert(typekey, btree);
static void InsInNode(btree, int);
static void SplitNode(btree, int);
static btree NewRoot(btree);
static void InternalDelete(typekey, btree);
static void JoinNode(btree, int);
static void MoveLeftNode(btree t, int);
static void MoveRightNode(btree t, int);
static void DelFromNode(btree t, int);
static btree FreeRoot(btree);
static btree delall(btree);
static void Error(int,typekey);
void out_txt(int * pt,int n);
int *read_txt(int n);
/* end of btrees.h */
/* btrees.c */
#include "btrees.h"
btree search(typekey key, btree t)
{
int i,j,m;
level=btree_level-1;
while (level >= 0){
for(i=0, j=t->d-1; i<j; m=(j+i)/2, (key > t->k[m])?(i=m+1):(j=m));
if (key == t->k [ i ]){
btree_disp = i;
return t;
}
if (key > t->k [ i ]) /* i == t->d-1 时有可能出现 */
i++;
t = t->p[ i ];
level--;
}
return NULL;
}
btree insert(typekey key, btree t)
{
level=btree_level;
InternalInsert(key, t);
if (flag == 1) /* 根节点满之后,它被分割成两个半满节点 */
t=NewRoot(t); /* 树的高度增加 */
return t;
}
void InternalInsert(typekey key, btree t)
{
int i,j,m;
level--;
if (level < 0){ /* 到达了树的底部: 指出要做的插入 */
NewTree = NULL; /* 这个键没有对应的子树 */
InsKey = key; /* 导致底层的叶子节点增加键值+空子树对 */
btree_count++;
flag = 1; /* 指示上层节点把返回的键插入其中 */
return;
}
for(i=0, j=t->d-1; i<j; m=(j+i)/2, (key > t->k[m])?(i=m+1):(j=m));
if (key == t->k[ i ]) {
Error(1,key); /* 键已经在树中 */
flag = 0;
return;
}
if (key > t->k[ i ]) /* i == t->d-1 时有可能出现 */
i++;
InternalInsert(key, t->p[ i ]);
if (flag == 0)
return;
/* 有新键要插入到当前节点中 */
if (t->d < 2*M) {/* 当前节点未满 */
InsInNode(t, i); /* 把键值+子树对插入当前节点中 */
flag = 0; /* 指示上层节点没有需要插入的键值+子树,插入过程结束 */
}
else /* 当前节点已满,则分割这个页面并把键值+子树对插入当前节点中 */
SplitNode(t, i); /* 继续指示上层节点把返回的键值+子树插入其中 */
}
/*
* 把一个键和对应的右子树插入一个节点中
*/
void InsInNode(btree t, int d)
{
int i;
/* 把所有大于要插入的键值的键和对应的右子树右移 */
for(i = t->d; i > d; i--){
t->k[ i ] = t->k[i-1];
t->v[ i ] = t->v[i-1];
t->p[i+1] = t->p[ i ];
}
/* 插入键和右子树 */
t->k[ i ] = InsKey;
t->p[i+1] = NewTree;
t->v[ i ] = InsValue;
t->d++;
}
/*
* 前件是要插入一个键和对应的右子树,并且本节点已经满
* 导致分割这个节点,插入键和对应的右子树,
* 并向上层返回一个要插入键和对应的右子树
*/
void SplitNode(btree t, int d)
{
int i,j;
btree temp;
typekey temp_k;
char *temp_v;
/* 建立新节点 */
temp = (btree)malloc(sizeof(node));
/*
* +---+--------+-----+-----+--------+-----+
* | 0 | ...... | M | M+1 | ...... |2*M-1|
* +---+--------+-----+-----+--------+-----+
* |<- M+1 ->|<- M-1 ->|
*/
if (d > M) { /* 要插入当前节点的右半部分 */
/* 把从 2*M-1 到 M+1 的 M-1 个键值+子树对转移到新节点中,
* 并且为要插入的键值+子树空出位置 */
for(i=2*M-1,j=M-1; i>=d; i--,j--) {
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
for(i=d-1,j=d-M-2; j>=0; i--,j--) {
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
/* 把节点的最右子树转移成新节点的最左子树 */
temp->p[0] = t->p[M+1];
/* 在新节点中插入键和右子树 */
temp->k[d-M-1] = InsKey;
temp->p[d-M] = NewTree;
temp->v[d-M-1] = InsValue;
/* 设置要插入上层节点的键和值 */
InsKey = t->k[M];
InsValue = t->v[M];
}
else { /* d <= M */
/* 把从 2*M-1 到 M 的 M 个键值+子树对转移到新节点中 */
for(i=2*M-1,j=M-1; j>=0; i--,j--) {
temp->k[j] = t->k[ i ];
temp->v[j] = t->v[ i ];
temp->p[j+1] = t->p[i+1];
}
if (d == M) /* 要插入当前节点的正中间 */
/* 把要插入的子树作为新节点的最左子树 */
temp->p[0] = NewTree;
/* 直接把要插入的键和值返回给上层节点 */
else { /* (d<M) 要插入当前节点的左半部分 */
/* 把节点当前的最右子树转移成新节点的最左子树 */
temp->p[0] = t->p[M];
/* 保存要插入上层节点的键和值 */
temp_k = t->k[M-1];
temp_v = t->v[M-1];
/* 把所有大于要插入的键值的键和对应的右子树右移 */
for(i=M-1; i>d; i--) {
t->k[ i ] = t->k[i-1];
t->v[ i ] = t->v[i-1];
t->p[i+1] = t->p[ i ];
}
/* 在节点中插入键和右子树 */
t->k[d] = InsKey;
t->p[d+1] = NewTree;
t->v[d] = InsValue;
/* 设置要插入上层节点的键和值 */
InsKey = temp_k;
InsValue = temp_v;
}
}
t->d =M;
temp->d = M;
NewTree = temp;
node_sum++;
}
btree delete(typekey key, btree t)
{
level=btree_level;
InternalDelete(key, t);
if (t->d == 0)
/* 根节点的子节点合并导致根节点键的数目随之减少,
* 当根节点中没有键的时候,只有它的最左子树可能非空 */
t=FreeRoot(t);
return t;
}
void InternalDelete(typekey key, btree t)
{
int i,j,m;
btree l,r;
int lvl;
level--;
if (level < 0) {
Error(0,key); /* 在整个树中未找到要删除的键 */
flag = 0;
return;
}
for(i=0, j=t->d-1; i<j; m=(j+i)/2, (key > t->k[m])?(i=m+1):(j=m));
if (key == t->k[ i ]) { /* 找到要删除的键 */
if (t->v[ i ] != NULL)
free(t->v[ i ]); /* 释放这个节点包含的值 */
if (level == 0) { /* 有子树为空则这个键位于叶子节点 */
DelFromNode(t,i);
btree_count--;
flag = 1;
/* 指示上层节点本子树的键数量减少 */
return;
} else { /* 这个键位于非叶节点 */
lvl = level-1;
/* 找到前驱节点 */
r = t->p[ i ];
while (lvl > 0) {
r = r->p[r->d];
lvl--;
}
t->k[ i ]=r->k[r->d-1];
t->v[ i ]=r->v[r->d-1];
r->v[r->d-1]=NULL;
key = r->k[r->d-1];
}
}
else if (key > t->k[ i ]) /* i == t->d-1 时有可能出现 */
i++;
InternalDelete(key,t->p[ i ]);
/* 调整平衡 */
if (flag == 0)
return;
if (t->p[ i ]->d < M) {
if (i == t->d) /* 在最右子树中发生了删除 */
i--; /* 调整最右键的左右子树平衡 */
l = t->p [ i ];
r = t->p[i+1];
if (r->d > M)
MoveLeftNode(t,i);
else if(l->d > M)
MoveRightNode(t,i);
else {
JoinNode(t,i);
/* 继续指示上层节点本子树的键数量减少 */
return;
}
flag = 0;
/* 指示上层节点本子树的键数量没有减少,删除过程结束 */
}
}
/*
* 合并一个节点的某个键对应的两个子树
*/
void JoinNode(btree t, int d)
{
btree l,r;
int i,j;
l = t->p[d];
r = t->p[d+1];
/* 把这个键下移到它的左子树 */
l->k[l->d] = t->k[d];
l->v[l->d] = t->v[d];
/* 把右子树中的所有键值和子树转移到左子树 */
for (j=r->d-1,i=l->d+r->d; j >= 0 ; j--,i--) {
l->k[ i ] = r->k[j];
l->v[ i ] = r->v[j];
l->p[ i ] = r->p[j];
}
l->p[l->d+r->d+1] = r->p[r->d];
l->d += r->d+1;
/* 释放右子树的节点 */
free(r);
/* 把这个键右边的键和对应的右子树左移 */
for (i=d; i < t->d-1; i++) {
t->k[ i ] = t->k[i+1];
t->v[ i ] = t->v[i+1];
t->p[i+1] = t->p[i+2];
}
t->d--;
node_sum--;
}
/*
* 从一个键的右子树向左子树转移一些键,使两个子树平衡
*/
void MoveLeftNode(btree t, int d)
{
btree l,r;
int m; /* 应转移的键的数目 */
int i,j;
l = t->p[d];
r = t->p[d+1];
m = (r->d - l->d)/2;
/* 把这个键下移到它的左子树 */
l->k[l->d] = t->k[d];
l->v[l->d] = t->v[d];
/* 把右子树的最左子树转移成左子树的最右子树
* 从右子树向左子树移动 m-1 个键+子树对 */
for (j=m-2,i=l->d+m-1; j >= 0; j--,i--) {
l->k[ i ] = r->k[j];
l->v[ i ] = r->v[j];
l->p[ i ] = r->p[j];
}
l->p[l->d+m] = r->p[m-1];
/* 把右子树的最左键提升到这个键的位置上 */
t->k[d] = r->k[m-1];
t->v[d] = r->v[m-1];
/* 把右子树中的所有键值和子树左移 m 个位置 */
r->p[0] = r->p[m];
for (i=0; i<r->d-m; i++) {
r->k[ i ] = r->k[i+m];
r->v[ i ] = r->v[i+m];
r->p[ i ] = r->p[i+m];
}
r->p[r->d-m] = r->p[r->d];
l->d+=m;
r->d-=m;
}
/*
* 从一个键的左子树向右子树转移一些键,使两个子树平衡
*/
void MoveRightNode(btree t, int d)
{
btree l,r;
int m; /* 应转移的键的数目 */
int i,j;
l = t->p[d];
r = t->p[d+1];
m = (l->d - r->d)/2;
/* 把右子树中的所有键值和子树右移 m 个位置 */
r->p[r->d+m]=r->p[r->d];
for (i=r->d-1; i>=0; i--) {
r->k[i+m] = r->k[ i ];
r->v[i+m] = r->v[ i ];
r->p[i+m] = r->p[ i ];
}
/* 把这个键下移到它的右子树 */
r->k[m-1] = t->k[d];
r->v[m-1] = t->v[d];
/* 把左子树的最右子树转移成右子树的最左子树 */
r->p[m-1] = l->p[l->d];
/* 从左子树向右子树移动 m-1 个键+子树对 */
for (i=l->d-1,j=m-2; j>=0; j--,i--) {
r->k[j] = l->k[ i ];
r->v[j] = l->v[ i ];
r->p[j] = l->p[ i ];
}
/* 把左子树的最右键提升到这个键的位置上 */
t->k[d] = l->k[ i ];
t->v[d] = l->v[ i ];
l->d-=m;
r->d+=m;
}
/*
* 把一个键和对应的右子树从一个节点中删除
*/
void DelFromNode(btree t, int d)
{
int i;
/* 把所有大于要删除的键值的键左移 */
for(i=d; i < t->d-1; i++) {
t->k[ i ] = t->k[i+1];
t->v[ i ] = t->v[i+1];
}
t->d--;
}
/*
* 建立有两个子树和一个键的根节点
*/
btree NewRoot(btree t)
{
btree temp;
temp = (btree)malloc(sizeof(node));
temp->d = 1;
temp->p[0] = t;
temp->p[1] = NewTree;
temp->k[0] = InsKey;
temp->v[0] = InsValue;
btree_level++;
node_sum++;
return(temp);
}
/*
* 释放根节点,并返回它的最左子树
*/
btree FreeRoot(btree t)
{
btree temp;
temp = t->p[0];
free(t);
btree_level--;
node_sum--;
return temp;
}
void Error(int f,typekey key)
{
if (f)
printf("Btrees error: Insert %d!\n",key);
else
printf("Btrees error: delete %d!\n",key);
}
int height(btree t)
{
return btree_level;
}
int count(btree t)
{
return btree_count;
}
double payload(btree t)
{
if (node_sum==0)
return 1;
return (double)btree_count/(node_sum*(2*M));
}
btree deltree (btree t)
{
level=btree_level;
btree_level = 0;
return delall(t);
}
btree delall(btree t)
{
int i;
level--;
if (level >= 0) {
for (i=0; i < t->d; i++)
if (t->v[ i ] != NULL)
free(t->v[ i ]);
if (level > 0)
for (i=0; i<= t->d ; i++)
t->p[ i ]=delall(t->p[ i ]);
free(t);
}
return NULL;
}
/* end of btrees.c */
void out_txt(int * pt,int n)
{
FILE *fp_b;
int i;
if((fp_b=fopen("btree2.txt","a"))==NULL)
{
printf("cannot open this file\n");
exit(0);
}
//fprintf(fp_b,"%d\t",bucket_volumes);
for (i=0;i<n;i++)
{
fprintf(fp_b,"%d\t",pt[i]);
}
fprintf(fp_b,"\r");
}
int *read_txt(int n)
{
FILE *fp;
int i;
int *a=(int *)malloc(n*sizeof(int));
if ((fp = fopen("F:\\text_data.txt","rt")) == NULL)
{
printf("open file failed!\n");
exit(1);
}
for (i=0; i<n; i++)
{
fscanf(fp,"%d", &a[i]);
// fprintf(fp,"%d ",a[i]);
}
fclose(fp);
return a;
}
#include "btrees.h"
#define key_num 1000
void main()
{
int * key_array;
int i;
int pt[5];
btree root,temp;
long long sf1,sf2,sf3;
LARGE_INTEGER f1,f2,f3,f5,f4,f6;
InsValue = NULL; /* 与要插的键相对应的值 */
/* 节点增减标志 */
btree_level = 0; /* 多路树的高度 */
btree_count = 0; /* 多路树的键总数 */
node_sum = 0; /* 多路树的节点总数 */
key_array=read_txt(key_num);
temp = (btree)malloc(sizeof(node));
temp->d = 0;
temp->p[0] = NewTree;
temp->p[1] = NewTree;
temp->k[0] = InsKey;
temp->v[0] = InsValue;
root=temp;
QueryPerformanceCounter(&f1);
for (i=0;i<key_num;i++)
{
root=insert(key_array[i],root);
}
QueryPerformanceCounter(&f2);
QueryPerformanceCounter(&f3);
for (i=0;i<key_num;i++)
{
search(key_array[i],root);
}
QueryPerformanceCounter(&f4);
QueryPerformanceCounter(&f5);
for (i=0;i<key_num;i++)
{
root=delete(key_array[i],root);
}
QueryPerformanceCounter(&f6);
sf1=f2.QuadPart-f1.QuadPart-750;
sf2=f4.QuadPart-f3.QuadPart-750;
sf3=f6.QuadPart-f5.QuadPart-750;
pt[0]=M+2;
pt[1]=key_num;
pt[2]=(sf1/1000)-7;
pt[3]=(sf2/1000)-7;
pt[4]=(sf3/1000)-7;
out_txt(pt,5);
Sleep(1000);
}