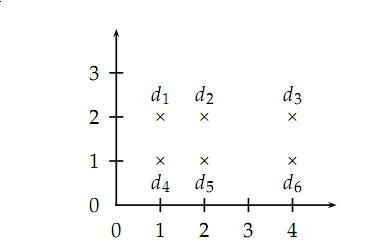聚类算法之K-means

区分两个概念：

hard clustering：一个文档要么属于类w，要么不属于类w，即文档对确定的类w是二值的1或0。

soft clustering：一个文档可以属于类w1，同时也可以属于w2，而且文档属于一个类的值不是0或1，可以是0.3这样的小数。

 

K-Means就是一种hard clustering，所谓K-means里的K就是我们要事先指定分类的个数，即K个。

 

k-means算法的流程如下：

1）从N个文档随机选取K个文档作为初始质心

2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类

3）重新计算已经得到的各个类的质心

 

4）迭代2～3步直至满足既定的条件，算法结束

 

在K－means算法里所有的文档都必须向量化，n个文档的质心可以认为是这n个向量的中心，计算方法如下：

这里加入一个方差RSS的概念：

RSSk的值是类k中每个文档到质心的距离，RSS是所有k个类的RSS值的和。

 

算法结束条件：

1）给定一个迭代次数，达到这个次数就停止，这好像不是一个好建议。

2）k个质心应该达到收敛，即第n次计算出的n个质心在第n＋1次迭代时候位置不变。

3）n个文档达到收敛，即第n次计算出的n个文档分类和在第n＋1次迭代时候文档分类结果相同。

4）RSS值小于一个阀值，实际中往往把这个条件结合条件1使用

 

 

回过头用RSS讨论质心的计算方法是否合理

为了取得RSS的极小值，RSS对质心求偏导数应该为0，所以得到质心

可见，这个质心的选择是合乎数学原理的。

 

K-means方法的缺点是聚类结果依赖于初始选择的几个质点位置，看下面这个例子：

如果使用2－means方法，初始选择d2和d5那么得到的聚类结果就是｛d1，d2，d3｝｛d4，d5，d6｝，这不是一个合理的聚类结果

解决这种初始种子问题的方案：

1）去处一些游离在外层的文档后再选择

2）多选一些种子，取结果好的（RSS小）的K个类继续算法

3）用层次聚类的方法选择种子。我认为这不是一个合适的方法，因为对初始N个文档进行层次聚类代价非常高。

 

 

以上的讨论都是基于K是已知的，但是我们怎么能从随机的文档集合中选择这个k值呢？

我们可以对k去1～N分别执行k-means，得到RSS关于K的函数下图：

当RSS由显著下降到不是那么显著下降的K值就可以作为最终的K，如图可以选择4或9。