bzoj1311: 最优压缩
传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=1311
思路:很明显的二元组建图
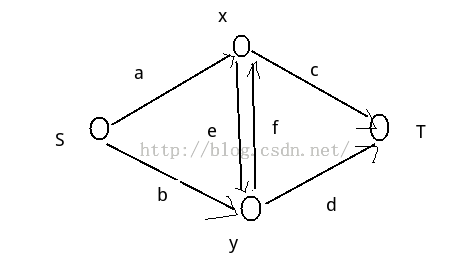
还是这个图,设与S相连表示设为V0,与T相连表示设为v1
列方程,设有两个相邻的点ij,注意一组ij只能算一次,所以两个1/2就并成1了
a+b=|A[i]-v0|+|A[j]-v0|
c+d=|A[i]-v1|+|A[j]-v1|
a+f+d=|A[i]-v0|+|A[j]-v1|+|A[i]-A[j]|
b+e+c=|A[i]-v1|+|A[j]-v0|+|A[i]-A[j]|
e=f=|A[i]-A[j]|
a=|A[i]-v0|
b=|A[j]-v0|
c=|A[i]-v1|
d=|A[j]-v1|
然后按这个建图就可以了
S向每个点连|A[i]-v0|的边,每个点向T连|A[i]-v1|的边,每组相邻的点(i,j)(i在j的左边或上面)连|A[i]-A[j]|的双向边
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define abs(a) (a>0?a:-(a))
const int dx[]={0,1};
const int dy[]={1,0};
const int N=50,maxn=1305,maxm=100010,inf=1061109567;
using namespace std;
int n,m,w[N][N],V0,V1,A[N][N],B[N][N];
inline int id(int x,int y){return (x-1)*m+y;}
struct Flow{
int pre[maxm],now[maxn],son[maxm],val[maxm],tot,dis[maxn],q[maxn+10],head,tail,S,T;
void add(int a,int b,int c){pre[++tot]=now[a],now[a]=tot,son[tot]=b,val[tot]=c;}
void ins(int a,int b,int c){add(a,b,c),add(b,a,0);}
void ins2(int a,int b,int c){add(a,b,c),add(b,a,c);}
void init(){memset(now,0,sizeof(now)),tot=1,S=0,T=maxn-1;}
void build(){
for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) ins(S,id(i,j),abs(w[i][j]-V0)),ins(id(i,j),T,abs(w[i][j]-V1));
for (int i=1;i<=n;i++) for (int j=1;j<=m;j++)
for (int k=0;k<=1;k++){
int nx=i+dx[k],ny=j+dy[k];
if (nx>n||ny>m) continue;
ins2(id(i,j),id(nx,ny),abs(w[i][j]-w[nx][ny]));
}
}
bool bfs(){
memset(dis,-1,sizeof(dis));
q[tail=1]=S,dis[S]=head=0;
while (head!=tail){
if (++head>maxn) head=1;
int x=q[head];
for (int y=now[x];y;y=pre[y])
if (dis[son[y]]==-1&&val[y]){
if (++tail>maxn) tail=1;
dis[son[y]]=dis[x]+1,q[tail]=son[y];
}
}
return dis[T]>0;
}
int find(int x,int low){
if (x==T) return low;
int y,res=0;
for (y=now[x];y;y=pre[y]){
if (dis[son[y]]!=dis[x]+1||!val[y]) continue;
int tmp=find(son[y],min(val[y],low));
res+=tmp,low-=tmp,val[y]-=tmp,val[y^1]+=tmp;
if (!low) break;
}
if (!y) dis[x]=-1;
return res;
}
void work(){
int res=0;
while (bfs()) res+=find(S,inf);
printf("%d\n",res);
}
}F;
int main(){
scanf("%d%d%d%d",&n,&m,&V0,&V1),F.init();
for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) scanf("%d",&w[i][j]);
F.build(),F.work();
return 0;
}