投影纹理映射(Projective Texture Mapping)
摘抄“GPU Programming And Cg Language Primer 1rd Edition” 中文 名“GPU编程与CG语言之阳春白雪下里巴人”
投影纹理映射( Projective Texture Mapping )最初由 Segal 在文章 “Fast shadows and lighting effects using texture maaping” 中提出,用于映射一个纹理到物体上,就像将幻灯片投影到墙上一样。该方法不需要在应用程序中指定顶点纹理坐标,实际上,投影纹理映射中使用的纹理坐标是在顶点着色程序中通过视点矩阵和投影矩阵计算得到的,通常也被称作投影纹理坐标 (coordinates in projective space) 。而我们常用的纹理坐标是在建模软件中通过手工调整纹理和 3D 模型的对应关系而产生的。
投影纹理映射的目的是将纹理和三维空间顶点进行对应,这种对应的方法好比 “ 将纹理当作一张幻灯片,投影到墙上一样 ” 。如 图 35 投影纹理映射 所示。
本章我们针对投影纹理映射的原理和实现方法进行详细的阐述。这一章的地位很高,在一些阴影算法以及体绘制算法中都需要用到投影纹理映射技术。严格的说,只要涉及到 “ 纹理实时和空间顶点对应 ” ,通常都会用到投影纹理映射技术。
12.1 投影纹理映射的优点
投影纹理映射有两大优点:其一,将纹理与空间顶点进行实时对应,不需要预先在建模软件中生成纹理坐标;其二,使用投影纹理映射,可以有效的避免纹理扭曲现象。
为了说明第一个优点,先举一个简要的例子:很多情况下,我们需要将场景渲染两遍,第一遍是为了获取场景信息,得到的场景信息通常保存为一张纹理(例如深度图);然后基于“存放场景信息”的纹理进行第二次渲染;第二次渲染结果才是最终显示到屏幕上的效果。为了在第二次渲染中使用到“存放场景信息”的纹理(无预先设置的纹理坐标),需要时时进行纹理计算,这时就可以使用投影纹理映射技术。实际上,这也是投影纹理映射技术的最广泛的应用了。
可能大家对于上一段文字还不能理解得很清楚,不过在第 13 章的阴影贴图算法以及第 15 章的体绘制光线投射算法中,大家会明白其含义。一个算法只有理论加实践,才可能真正的被理解,只会照本宣科的朗诵术语,基本上都是鲁迅先生所说的 “ 泥塘 ” 似的人。
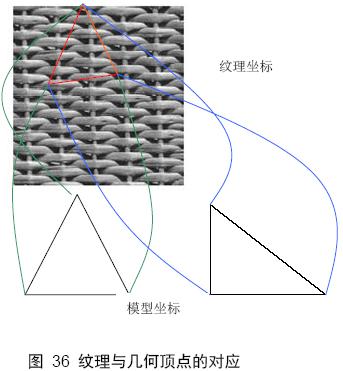
投影纹理映射的第二个优点是:可以有效的避免纹理扭曲现象。如 图 36 所示,将一张纹理投影到两个三角面片上,它们的顶点纹理坐标相同,但是由于三角面片形状不同,插值出来的内部点的纹理坐标也会产生不同的梯度( gradient ),最后纹理颜色在两个三角面片上的分布也是不一样的。
图 37 右边所示的是将一张纹理贴到一个正方形上,左边所示的是将同样的纹理贴到一个梯形上,正方形和梯形的顶点纹理坐标相同,但两者的贴图效果是不同的。梯形上的纹理会出现明显的扭曲现象。这是因为几何体的变换,导致插值出来的内部纹理坐标分布不均衡。
12.2 齐次纹理坐标( Homogeneous Texture Coordinates )
齐次纹理坐标( homogeneous texture coordinates )的概念对大多数人来说比较陌生,纹理坐标一般是二维的,如果是体纹理,其纹理坐标也只是三维的。齐次纹理坐标的出现是为了和三维顶点的齐次坐标相对应,因为本质上,投影纹理坐标是通过三维顶点的齐次坐标计算得到的。
齐次纹理坐标通常表示为(s,t,r,q ), 以区别于物体位置齐次坐标(x, y, z, w) 。一维纹理常用s 坐标表示,二维纹理常用(s, t) 坐标表示,目前忽略r 坐标,q 坐标的作用与齐次坐标点中的w 坐标非常类似。值一般为1 。
12.3 原理与实现流程
对投影纹理映射,很多教程上都是这么解释的:纹理好比一张幻灯片,灯光好比投影机,然后将纹理投影到一个物体上,类似于投影机将幻灯片投影到墙上。这个比喻没有太大的问题,也找不到更加形象的比喻了。问题是:这个解释刚好颠倒了算法的实现流程。
投影纹理映射真正的流程是 “ 根据投影机(视点相机)的位置、投影角度,物体的坐标,求出每个顶点所对应的纹理坐标,然后依据纹理坐标去查询纹理值 ” ,也就是说,不是将纹理投影到墙上,而是把墙投影到纹理上。投影纹理坐标的求得,也与纹理本身没有关系,而是由投影机的位置、角度,以及 3D 模型的顶点坐标所决定。所以,我一直觉得 “ 投影纹理映射 ” 这个术语具有很强的误导性,总让人觉得是把纹理投射出去。
根据顶点坐标获得纹理坐标的本质是将顶点坐标投影到 NDC 平面上,此时投影点的平面坐标即为纹理坐标。如果你将当前视点作为投影机,那么在顶点着色程序中通过 POSTION 语义词输出的顶点投影坐标,就是当前视点下的投影纹理坐标没有被归一化的表达形式。
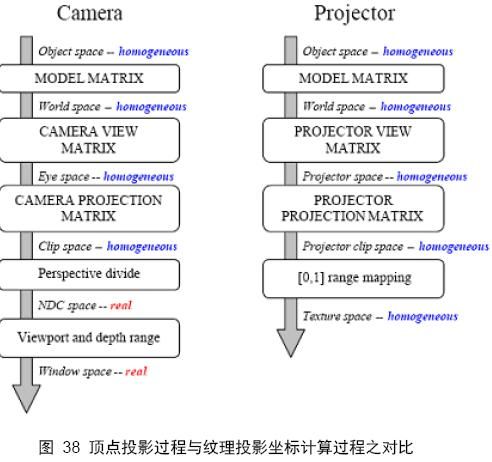
“Projective texture mapping” 文章中有一幅比较著名的图片,说明计算纹理投影坐标的过程,如 图 38 所示。
图 38 左边是正常的顶点坐标空间转换流程,无非是顶点从模型坐标空间转换到世界坐标空间,然后从世界坐标空间转换到视点空间,再从视点空间转换到裁剪空间,然后投影到视锥近平面,经过这些步骤,一个顶点就确定了在屏幕上的位置。图的右边是将视点当作投影机,根据模型空间的顶点坐标,求得投影纹理坐标的流程。通过比较,可以发现这两个流程基本一样,唯一的区别在于求取顶点投影坐标后的归一化不一样:计算投影纹理坐标需要将投影顶点坐标归一化到【0 ,1 】空间中,实现这一步,可以在需要左乘矩阵normalMatrix , 也可以在着色程序中对顶点投影坐标的每个分量先乘以1/2 然后再加上1/2 。
所以求取投影坐标矩阵的公式为:
求得纹理投影矩阵后,便可以使用该矩阵将顶点坐标转换为纹理投影坐标。
使用投影纹理坐标之前,别忘了将投影纹理坐标除以最后一个分量 q 。到此,你就可以使用所求得的投影纹理坐标的前两个分量去检索纹理图片,从中提取颜色值。还记得Cg 标准函数库中有的纹理映射函数的表达形式为:
tex2DProj(sampler2D tex, float4 szq)
tex2DProj 函数与 tex2D 函数的区别就在于:前者会对齐次纹理坐标除以最后一个分量 q ,然后再进行纹理检索!
注意:上面常被提到的“投影机”只是一种形象化的比喻,本质是视点相机,很多教程上都说“将灯光当作投影机”,这是一种错误的表达(并非是这些教程的作者不懂,而是语言组织上的错误),他们真正的意思是“在当前灯光所在的位置放置一个相机,相机的观察方向和光线投射方向一致”,这个相机就作为投影机使用。在一些阴影算法中,根据光源信息设置投影机,并从投影机的角度渲染出场景信息纹理(如,阴影纹理),然后把这个纹理放到正常的场景渲染相机中使用,这时就需要投影机的矩阵信息来建立投影纹理矩阵了。
附:投影纹理矩阵的计算通常不需要开发人员自己动手,常用的图形API 中都给出了获取各种矩阵(视点矩阵、投影矩阵等)的函数,不过偏移矩阵需要自己设置。在应用程序中获取这些矩阵信息后,再传递到着色程序中使用。
顶点着色程序和片段着色程序如下所示:
代码 16 投影纹理映射顶点着色程序
void main_v(
float4 position : POSITION,
float4 normal : NORMAL,
out float4 outPos : POSITION,
out float4 outShadowUV : TEXCOORD0,
uniform float4x4 worldMatrix,
uniform float4x4 worldViewProj,
uniform float4x4 texViewProj // 投影纹理矩阵
)
{
outPos = mul(worldViewProj, position);
// 计算投影纹理坐标
float4 worldPos = mul(worldMatrix, position);
outShadowUV = mul(texViewProj, worldPos);
}
代码 17 投影纹理映射片段着色程序
void main_f(
float4 shadowUV : TEXCOORD0,
out float4 result : COLOR,
uniform sampler2D projectiveMap // 用于投影的纹理
)
{
shadowUV = shadowUV / shadowUV.w;
float4 mapColor ;
// 归一化到 0-1 空间
shadowUV.x = (shadowUV.x +float(1.0))/float(2.0);
shadowUV.y = (shadowUV.y +float(1.0))/float(2.0);
mapColor = tex2D(projectiveMap, shadowUV.xy);
result = mapColor;
}