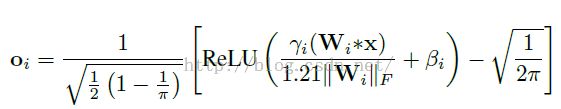论文心得:BatchNorm的那些变体
本文记录BatchNormalization的三个拓展,分别是AdaBN(Revisiting Batch Normalization For PracticalDomain Adaptation)、WeightNormalization(Weight Normalization: A Simple Reparameterizationto Accelerate Training of Deep Neural Networks)、NormalizationPropagation(Normalization Propagation: A Parametric Technique for Removing Internal Covariate Shift in Deep Networks)。
0.回顾BatchNormalization
该层的设计是为了解决Internal Covariate Shift的问题,公式如下:
因为输入变得很稳定,促进了模型的收敛并一定程度上阻止了过拟合,作者猜测BatchNormalization层的雅可比矩阵的奇异值接近1,这加速了模型的收敛速度。
实际用的时候再加入scale和shift,使得BN能够表达identity,这样卷积层inference时就不再依赖于miniBatch,如下式所示: 通常将带scale和shift的BN层加在非线性激活函数之前,在caffe的官方版本中没有这两个自学习参数(但有一个scale层可以组合使用),因此一般将其加在非线性函数之后,否则weight层的bias就白学了(非官方解释)。 BN的两个缺陷也很明显,因为是对mini-batch求统计信息,因此具有数据依赖性,数据的随机性会导致训练的不稳定,且batch=1时无法使用。1.AdaBN
这个变体不是为了解决BN带来的缺陷,而是解决了一个BN没能很好解决的问题,就是当训练图像和测试图像不是同一个源时,需要不小的数据集进行finetune,AdaBN采用了一个简单粗暴的方法缓解了跨域的transfer learning,即domain adaption问题,公式如下:

其中j表示每一个神经元。 作者在实验中验证了该方法的有效性,adaption之后训练域和测试域的数据混杂地更为均衡,同时同一层的神经元之间的KL离散度降低,减小了域的差异。然而作者并没有给出详细的理论性的解释。 下表是KL离散度的对比:

作者将每个neuron的权值normalize为1,weight的优化便以另一种表达: 
更新公式如下: 如此便解耦了权重向量的范数和方向,加速了收敛,保证了gradient的稳定,不会爆炸或者消失;同时解决了BN的数据依赖性,计算开销也降低了许多。 相比于BN,该方法没能将每一层特征尺度固定住,因此作者设计了一种初始化方法,在初始化时利用了mini-batch的信息,保证了features在初始化时为0均值,1方差。 作者在实验部分验证了该方法在CIFAR-10、Convolutional VAE、DRAW、DQN等模型中都取得了更好的结果;作者同时提出了两个extensions,一个是对参数g引入log-scale的参数s,即$g=e^(cs)$;一个是给v的范数设定一个范围,这样虽然延长了参数更新,但收敛后的测试性能会比较好。
3.NormalizationPropagation
该方法的论文详细论述了比WeightNormalization更多的理论意义和直观解释,主要思想就是对输入数据做normalization,然后将normalization的效果传递到后续的层中,下式是对该方法有效性的理论分析命题: 由上式可以看出:1)协方差矩阵近似是一个误差有界的对角矩阵,误差大小由W控制2)如果希望u有单位方差,则要除一个$||W_i||_2^2$,这实际上就是对WeightNormalization做出了解释。上式中的bound第一项在W归一化后为0了,第二项是与W的coherence(即列矩阵的相关系数)有关,而真实的数据确实比较低,这便又印证了1)。 下式以Relu为例,给出了数据进过非线性单元后的调整: 然后,作者严格地论述了NormalizationPropagation的雅可比矩阵的奇异值接近1(1.21)。最后给出了完整的全连接和卷积层的变换公式: 图1是试验中的各层mean对比,NormProp的各层mean达到稳定的速度更快且更接近0:
4.后言
综上,Normalization在深度网络中的价值是值得深度挖掘下去的。正如WeightNormalization文中提到的,从优化方面,基于一阶梯度的优化高度依赖于目标函数的曲率,如果目标在最优点的hessian矩阵的条件数太小,就是病态曲率,不同的参数化方法就会导致不同的曲率,通过Normalization来优化参数化的方法也不失为一个好的策略。