[计算机视觉:算法与应用]学习笔记一:图像形成
1. 2D点可以利用一对值(x,y)来表示,也可以利用齐次坐标来表示,那么什么是齐次坐标?用齐次坐标表示有什么优势?
参考:参考百度百科【齐次坐标】
# 二维点(x,y)的齐次坐标表示为(hx,hy,h)。由此可以看出,一个向量的齐次表示是不唯一的,齐次坐标的h取不同的值都表示的是同一个点,比如齐次坐标(8,4,2)、(4,2,1)表示的都是二维点(4,2)。
# 齐次坐标正常化处理(点的齐次表达式转换为二维笛卡尔坐标):
[X,Y,H]->[X/H,Y/H,1]=[x,y,1].
几何上的解释可以看成:发生在三维空间的变换限制在H=1的平面内。
# 引进齐次坐标,有什么必要呢???
几何变换,主要包括平移、旋转、缩放。以矩阵表达式来计算这些变换时,平移是矩阵相加;缩放和旋转是矩阵相乘。综合起来,对于一个刚体,几何变换可以形容为Rigid_after=Matrix1*Rigid_before+Matrix2.其中,Matrix1是旋转和缩放矩阵;Matrix2是平移矩阵。
引入齐次坐标的主要目的就是,合并矩阵运算中的乘法和加法。
2. 2D图像仿射变换(Affine)及自由度?
二维仿射变换是一种二维坐标到二维坐标的线性变换,保持了二维图像的“平直性”(straightness:即变换之后,直线还是直线,圆弧还是圆弧)和“平行性”(parallelness:图像间的位置保持不变,平行关系不改变,线上点的顺序不改变)。向量之间的夹角会发生改变。
仿射变换可以通过一系列的子变换的复合形式构成。
#2D 平移变换(2个自由度)
#2D 旋转变换(3个自由度)
#2D 缩放
#2D 剪切
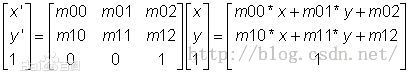
![[计算机视觉:算法与应用]学习笔记一:图像形成_第1张图片](http://img.e-com-net.com/image/info5/a9125d19d2724c2882b2c9182e2505d3.jpg)
![[计算机视觉:算法与应用]学习笔记一:图像形成_第2张图片](http://img.e-com-net.com/image/info5/02716f57f1c04f499d75349324ca695b.jpg)
![[计算机视觉:算法与应用]学习笔记一:图像形成_第3张图片](http://img.e-com-net.com/image/info5/cfcd2d6ab658422393d3d68cc42449e2.jpg)