排序算法分析归纳总结
排序方法分类:
按照策略 划分内部排序方法为五大类:
插入排序、选择、交换、归并 和 分配排序。
下面我了归纳上述类型的排序算法和其他经典算法。
以下默认升序!!
插入排序:
直接插入排序:
排序思想:
将所有数据放入数组R[1 ... n]中,初始状态R[1]是有序区,无序区为R[2 .. n],从R[1... n]经过比较依次插入R[1]有序区中,得到一个有序序列。
那么按照定义来写:
<span style="font-family:Microsoft YaHei;font-size:14px;">void InsertSort(int a[],int n)
{
int i,j,k;
for(i = 1;i< n;i++) //初始的有序区为a[0],所以待插入数从a[1]开始。
{
for(j = i-1;j >= 0;j--) //在有序区中找到a[1]插入的位置
{
if(a[i]>a[j])
break;
}
if(j!= i-1) //如果找到的位置是原位,则说明待插入数也将加入有序区。
{
int temp = a[i];
for(k = i;k>j;k--) //标记待插入的数的值,然后从此一直到要插入的位置进行移位
{
a[k] = a[k-1];
}
a[k+1] = temp; //移位完成后插入数据。
}
}
}</span>
代码优化:
首先,我们可以将if(a[j]< a[i])这条语句加入到第二层for循环的判断中,考虑到如果,要插入的数据比有序区的最后一位要小,是不用执行移位、插入操作的,所以得到优化过后的代码:
<span style="font-family:Microsoft YaHei;font-size:14px;">void InsertSort(int a[],int n)
{
int i,j,k;
for(i = 1;i< n;i++)
{
if(a[i] <a[i-1])
{
int temp = a[i];
for(j = i-1;j >= 0 && a[j] > a[i];j--)
{
a[j+1] = a[j];
}
a[j+1] = temp;
}
}
}</span>
算法分析:
1.算法的时间性能分析
对于具有n个数据,要进行n-1趟排序。
各种状态下的时间复杂度:
│ 初始状态 正序 反序 无序(平均)
│ 第i趟的关键 1 i+1 (i-2)/2
比较次数
│总比较次数 n-1 (n+2)(n-1)/2 ≈n2/4
│第i趟记录移动次数 0 i+2 (i-2)/2
│总的记录移动次数 0 (n-1)(n+4)/2 ≈n2/4
│时间复杂度 0(n) O(n2) O(n2)
注意:
按递增有序,简称"正序"。
按递减有序,简称"反序"。
2.算法的空间复杂度分析
算法所需的辅助空间是一个监视哨,辅助空间复杂度S(n)=O(1)。是一个就地排序。
3.直接插入排序的稳定性
直接插入排序是稳定的排序方法。
希尔排序:
排序思想:取一个小于n 的正整数d1,然将数据分为d1组,所有相距d1距离的数据元素为同一组元素,在同一个组内进行直接插入排序,然后取第二个增量d2(小于d1)重复此操作,直至所取的增量为1,即:所有的元素放在同一组 内进行直接插入排序。
该方法的实质:分组插入排序。要知道 的是:希尔排序只会在最后一趟排序后生成有序 序列,在此之前 ,希尔排序并不会生成 有序区 ,但是每趟排序之后,都会逼近 有序序列。
code:
严格 按照定义:
<span style="font-family:Microsoft YaHei;font-size:14px;">void ShellSort(int a[],int n)
{
int temp;
int i,j;
int gap = n/2;
while(gap > 0)
{
for(i = gap;i<n;i++)
{
temp = a[i];
for(j = i- gap;j>=0&&temp > a[j];)
{
a[j+ gap] = a[j];
j = j- gap;
}
a[j+gap] = temp;
}
gap = gap/2;
}
}</span>
以n=10的一个数组49, 38, 65, 97, 26, 13, 27, 49, 55, 4为例:
第一次:gap = n/2 = 5;
49 38 65 97 26 13 27 49 55 4
1 2 3 4 5 1 2 3 4 5
在这里相同数字标记的为同一组元素,那么久将这10个数据分为 {49, 13},{38,27},{65,49},{97,55},{26,4}这五组数据,分别在组内进行直接插入排序, 得到排序结果{13,49},{27,38},{49,65},{55,97},{4,26}.还原到原来的同一组是数据为:
13,27,49,55,4,49,38,65,97,26
第二次:gap = gap/2 = 2;
13,27,49,55,4,49,38,65,97,26
1 2 1 2 1 2 1 2 1 2
分为两组:{13,49,4,38,97,} 和{27,55,49,65,26}这两组数组,在组内分别执行直接插入排序得到:{4,13,38,49,97},{26,27,49,55,65},还原到同一组:
4,26,13,27,38,49,49,55,97,65,
第三次排序:gap = gap/2 = 1
4,26,13,27,38,49,49,55,97,65,
1 1 1 1 1 1 1 1 1 1
那么这就意味一所有数据处于同一组数据中,直接一趟直接插入排序得到最终结果:
得到最终数据:
4 13 26 27 38 49 49 55 65 97
希尔排序的时间复杂度是所取增量的序列的函数,而增量的选取是无法确定的,所以造成希尔排序的时间复杂度是难以确定的,但是一般认为希尔排序的平均时间复杂度为O(n的1.3次方);
希尔排序与直接插入排序的比较:
希尔排序的时间性能优于直接插入排序,原因:
1.数据基本有序的时候直接插入排序所需要的比较和移动次数较少
2.当n值较少时,n的平方与n 的差距也较小,所有直接插入排序算法的最好时间复杂度为O(n),最坏时间复杂度为O(n 的平方)
3.希尔排序当初始时增量大,分组较多,导致直接插入排序较快,而当增量减小时,分组较少,但是每一句都趋近与有序序列,导致直接插入 排序较快,
因此希尔排序在直接插入排序中有很大的改进,
希尔排序是不稳定的。
交换排序:
冒泡排序:
排序思想 :
总体来说:对于一组数据,先遍历一次找到最小的,放在R[0]处,然后第二次遍历找到第二小的放在R[1]处。依次类推。
细节来说:
给一组数据:,5 2 3 4 1,此时:标记 i = a[0] = 5;
第一次排序:
5 比 2 小,则2 于 5 交换,i = a[0 = 2]得到:2 5 3 4 1
第二次比较:
2 比3小。不交换位置
第三次比较:
2比四小,不交换位置;
第五次比较:
2 比1 小,交换位置:得到:1 5 3 4 2,
依次类推 最终得到结果:1 2 3 4 5.
即每一次排序都将一个值放在他应在的位置上去。
<span style="font-family:Microsoft YaHei;font-size:14px;">void BubbleSort(int a[].int n)
{
int i,j;
for(i = 0;i< n - 1;i++)
{
for(j = i+1;j<n;j++)
{
if(a[i] > a[j])
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}</span>
其他方式:
既然,冒泡排序算法每次将最无序区中最小的元素 上浮到 最前面,称为有序区的一部分,那么每次 比较的都是有序区以后 的部分,相当于说,我们可以 从数据末尾到无序区开始范围内 进行比较,(倒着来)
code:
<span style="font-family:Microsoft YaHei;font-size:14px;">void BubbleSort(int a[].int n)
{
int i,j;
for(i = 0;i < n - 1;i++)
{
for(j = n-1;j > i;j--)
{
if(a[i] > a[j])
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}</span>
代码优化:
这样倒着来的时候,我们可以将算法进一步的优化。这是因为此时每趟排序中 都 会有 位置的交换操作发生,如果没有发生,则说明无序区的所有位置都相对是有序的,即:无序区是有序的,那么可以说明整个数据是有序的(因为有序区的最后的一个数是小于无序区最小元素的值的),那么我们可以设置一个变量来检测此行为:
<span style="font-family:Microsoft YaHei;font-size:14px;">void BubbleSort(int a[].int n)
{
int i,j;
for(i = 0;i < n - 1;i++)
{
bool isOver = true;
for(j = n-1;j > i;j--)
{
if(a[i] > a[j])
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
isOver = false;
}
}
if(isOver == true)
{
return ;
}
}
}</span>
分析:
若初始文件是反序的,需要进行(n-1)
快速排序:
| 0 |
1 |
2 |
3 |
4 |
| 22 |
4 |
96 |
30 |
13 |
| 0 |
1 |
2 |
3 |
4 |
| 13 |
4 |
96 |
30 |
13 |
| 0 |
1 |
2 |
3 |
4 |
| 13 |
4 |
96 |
30 |
96 |
| 0 |
1 |
2 |
3 |
4 |
| 13 |
4 |
22 |
30 |
96 |
<span style="font-family:Microsoft YaHei;font-size:14px;">void QuickSort(int a[], int l, int r)
{
if (l < r){
int i = l;
int j = r;
int X = a[l];
while (i < j)
{
while (i < j && a[j] >= X)
j--;
if (i < j)
{
a[i++] = a[j];
}
while (i < j && a[i] < X)
{
i++;
}
if (i < j)
{
a[j--] = a[i];
}
}
a[i] = X;
QuickSort(a, l, i - 1);
QuickSort(a, i + 1, r);
}
}</span>
<span style="font-family:Microsoft YaHei;font-size:14px;">void QuickSort(int a[], int l, int r)
{
if (l < r){
int i = l;
int j = r;
//Swap(a[l], a[(l + r) / 2]); //首元素和中间元素调换位置
int X = a[l];
while (i < j)
{
while (i < j && a[j] >= X)
j--;
if (i < j)
{
a[i++] = a[j];
}
while (i < j && a[i] < X)
{
i++;
}
if (i < j)
{
a[j--] = a[i];
}
}
a[i] = X;
QuickSort(a, l, i - 1);
QuickSort(a, i + 1, r);
}
}</span>
算法分析:
快速排序每次将待排序数组分为两个部分,在理想状况下,每一次都将待排序数组划分成等长两个部分,则需要logn次划分。
而在最坏情况下,即数组已经有序或大致有序的情况下,每次划分只能减少一个元素,快速排序将不幸退化为冒泡排序,所以快速排序时间复杂度下界为O(nlogn),最坏情况为O(n^2)。在实际应用中,快速排序的平均时间复杂度为O(nlogn)。
快速排序在对序列的操作过程中只需花费常数级的空间。空间复杂度S(1)。
但需要注意递归栈上需要花费最少logn最多n的空间。
选择排序:
直接选择排序:
void SelectSort(int a[], int n)
{
int i, j, k;
for (i = 0; i < n -1;i++)
{
k = i;
for (j = i + 1; j < n; j++)
{
if (a[j] < a[k])
{
k = j;
}
}
int temp = a[i];
a[i] = a[k];
a[k] = temp;
}
}
总的移动次数 3(n-1).由此可知,直接选择排序的时间复杂度为 O(n2) (n的平方),所以当记录占用字节数较多时,通常比直接插入排序的执行速度快些。
由于在直接选择排序中存在着不相邻元素之间的互换,因此,直接选择排序是一种不稳定的排序方法。
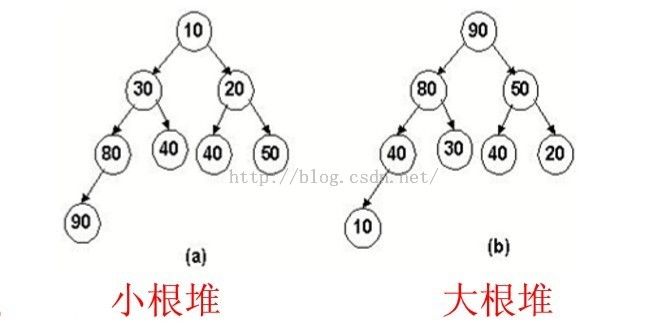
n个关键字序列Kl,K2,…,Kn称为堆,当且仅当该序列满足如下性质(简称为堆性质): (1) ki≤K2i且ki≤K2i+1 或(2)Ki≥K2i且ki≥K2i+1。
堆的性质:
由定义可以得出,堆的父节点总是大于等于或者小于等于它的子节点;每个节点的左儿子和有儿子又都是一个二叉堆;
二叉堆分为两种:
1.最大堆:父节点的值大于等于子任何一个子节点的值时的二叉堆
2.最小堆:父节点的值小于等于任何一个子节点的值时的二叉堆。
最小堆和最小堆的示例:
下面已最大堆为例子:
最大堆对应 的就是挑选 最大元素,将数组看为一颗完全二叉树,那么此时我们 可以利用完全二叉树的父亲与孩子节点的关系来选择最大元素,
首先我们 把数据放在R[1...n]中(为了与二叉树的顺序储存结构相一致,堆排序的开始下边标从1开始),把每个数据看做一个我节点,那么首元素R[1]则为完全二叉树的根,以下元素依次每层从左到右排列在数组 中,R[i]的左孩子是R[2i],右节点R[2i+1];
堆排序的首要任务是 建堆,假设现在完全二叉树中的某个节点i,(左子树2i,右子树2i +1),我们需要将它的左子树和右子树和此i节点比较选取最大者当做这三个数的父节点,当然,这样比较后交换位置后可能会造成下一级的堆被破坏,所以我们需要接着按照上述方法进行下一级的建堆,直到完全二叉树中的节点i构成堆为止。对于任意一颗完全二叉树,i取[n/2]~1,反复利用此方法建堆。大数上调,小数下降,
调整堆的方法:
void Sift(int a[], int low, int high)
{
int i = low;
int temp = a[i];
int j = 2 * i;
while (j <= high)
{
if (j < high &&a[j] < a[j + 1]) //判断两个孩子节点哪个大(要注意此时判断的j是不能加上=号的。因为j代表左孩子节点,理论上还有j+1)
{
j++;
}
if (a[j] > temp) //如果最大的孩子节点比父节点大的话,
{
a[i] = a[j]; //<span style="font-family: Arial, Helvetica, sans-serif;">让其成为父节点</span>
i = j; //接着该节点往下进行建堆
j = 2 * i;
}
else
break;
}
a[i] = temp;
}
在初始化堆构造后,最大的数一定位于根节点,将其放在序列的最后,也就是第一个数和最后一个数进行交换,由于最大的元素已经归位,所以待排序的数据中就减少了一位。但由于根节点的改变,这n-1个节点不一定还是堆,所以要再次初始化建堆,初始化建堆之后其根节点为次大的数据,将它放在序列的倒数第二位。如此反复的进行操作,知道完全二叉树只剩下一个根为止。
实现堆排序的算法如下:
void HeapSort(int a[], int n)
{
int i;
for (i = n / 2; i >= 1; i--)
{
Sift(a, i, n);
}
for (i = n; i >= 2; i--)
{
int temp = a[1];
a[1] = a[i];
a[i] = temp;
Sift(a, 1, i - 1);
}
}
算法模拟:
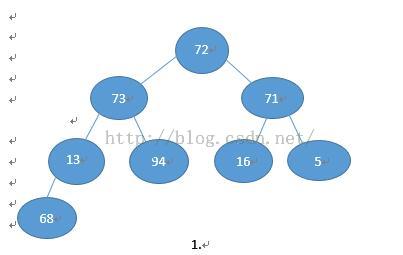
数据: 72 73 71 23 94 16 5 68
对应的完全二叉树1.:
模拟堆排:
初始时 i= n/2 = 4;j = i*2;那么68比13小,交换位置,j > n结束。
i 执行i--;i = 3;j = i*2 = 6,那么16 和5都比71小,直到j > n都未发生交换,结束,
4.i 执行 i--;i = 2;j = i*2 =4;那么 94比68和73大,执行73与94的交换,直到j>n;结束。
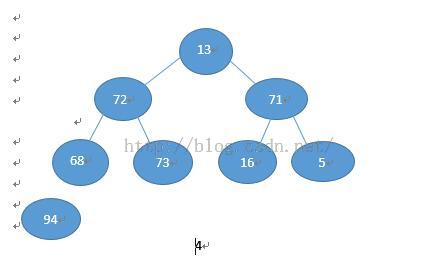
执行i--;i = 1;j = i*2 = 2;那么94比71 和72 大,成为父节点,直到j >n结束:
那么该建堆就结束了,可以看到最大的值是在根节点,我们将94与13交换,然后截断94的连接点,那么94就相当于已经归位,我们需要做的是将切断后的数据重新建堆,
找出次大的数。一直重复此操作,就可以得到有序序列。
完整代码:
void Sift(int a[], int low, int high)
{
int i = low;
int temp = a[i];
int j = 2 * i;
while (j <= high)
{
if (j < high &&a[j] < a[j + 1])
{
j++;
}
if (a[j] > temp)
{
a[i] = a[j];
i = j;
j = 2 * i;
}
else
break;
}
a[i] = temp;
}
void HeapSort(int a[], int n) //使用时调用此函数即可。
{
int i;
for (i = n / 2; i >= 1; i--)
{
Sift(a, i, n);
}
for (i = n; i >= 2; i--)
{
int temp = a[1];
a[1] = a[i];
a[i] = temp;
Sift(a, 1, i - 1);
}
}
算法分析:直接选择 排序中,为了从R[1..n]中选出最大的数据,必须进行n-1次比较,然后在R[2..n]中选出最大的数据需要执行n-2次比较,事实上,这些比较中有很多都是在重复比较。有很多比较可能已已经在n-1次比较中进行了,但由于未保留比较后的结果,所以执行了重复性的比较工作,而堆排序会对比较过后的结果进行保留,(根据上面的图例就可以看出来),减少了一些重复的比较。
时间复杂度:
堆排序的运行时间打过消耗在初始化建堆和重建堆的反复筛选中。二叉树从最底层右边的非终结点开始建堆,将其与其孩子进行比较和可能的交换,对于每个非终结点点来谈,最多进行量次比较和交换数据操作。在排序时(此时已经初始化建堆完成了),第i次去最大值记录重建堆需要O(logi)时间,并且需要取n-1次堆顶记录,所以重建堆的时间复杂度为O(nlogn)。
总体说:堆排序的时间复杂度为O(nlogn);
归并排序:
归并排序就是将若干个已经排好序的数据集合合并为一个数据聚合。
排序思想:
假设现在有两个已经排序的数组,要合并到同一个数组,那么我们就新建另一个数组来储存最终结果,依次比较R[i] 和A[j]的大小,将小的元素存进去,同时更新下标i或者j,如果有一个数组先比较完了,那么久将另一个数组剩下的全部复制在最终数组中去。
归并排序没什么好讲的,直接上代码:
void Marge(int a[], int n, int r[], int m,int t[])
{
int i = 0, j = 0, k = 0;
while (i < n &&j < m)
{
if (a[i] < r[j])
t[k++] = a[i++];
else
{
t[k++] = r[j++];
}
}
while (i < n)
{
t[k++] = a[i++];
}
while (j < m)
{
t[k++] = r[j++];
}
}这是简单的有序的归并排序。
未完,明天接着写。