数据降维方法分类

http://blog.csdn.net/xiaowei_cqu/article/details/7522368

数据降维基本原理是将样本点从输入空间通过线性或非线性变换映射到一个低维空间，从而获得一个关于原数据集紧致的低维表示。

数据降维工具箱drtoolbox中众多算法，这里简单做个分类。

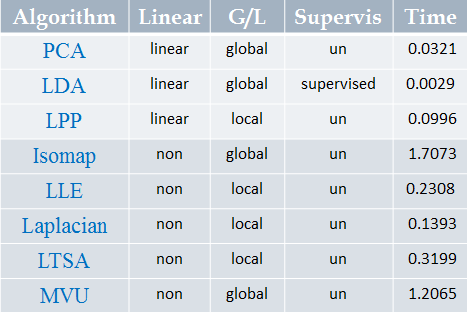
因为很多并没有仔细了解，在此次只对八种方法做分类：主成分分析（Principal Component Analysis,PCA)、线性判别分析（Linear Discriminant Analysis,LDA）、等距映射（Isomap）、局部线性嵌入（Locally Linear Embedding,LLE）、Laplacian 特征映射（Laplacian Eigenmaps）、局部保留投影（Local Preserving Projection,LPP）、局部切空间排列（Local Tangent Space Alignment,LTSA）、最大方差展开（ Maximum Variance Unfolding,MVU）

线性/非线性

线性降维是指通过降维所得到的低维数据能保持高维数据点之间的线性关系。线性降维方法主要包括PCA、LDA、LPP（LPP其实是Laplacian Eigenmaps的线性表示）；非线性降维一类是基于核的，如KPCA，此处暂不讨论；另一类就是通常所说的流形学习：从高维采样数据中恢复出低维流形结构（假设数据是均匀采样于一个高维欧式空间中的低维流形），即找到高维空间中的低维流形，并求出相应的嵌入映射。非线性流形学习方法有：Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU

整体来说，线性方法计算块，复杂度低，但对复杂的数据降维效果较差。

监督/非监督

监督式和非监督式学习的主要区别在于数据样本是否存在类别信息。非监督降维方法的目标是在降维时使得信息的损失最小，如PCA、LPP、Isomap、LLE、Laplacian Eigenmaps、LTSA、MVU；监督式降维方法的目标是最大化类别间的辨别信，如LDA。事实上，对于非监督式降维算法，都有相应的监督式或半监督式方法的研究。

全局/局部

局部方法仅考虑样品集合的局部信息，即数据点与临近点之间的关系。局部方法以LLE为代表，还包括Laplacian Eigenmaps、LPP、LTSA。

全局方法不仅考虑样本几何的局部信息，和考虑样本集合的全局信息，及样本点与非临近点之间的关系。全局算法有PCA、LDA、Isomap、MVU。

由于局部方法并不考虑数据流形上相距较远的样本之间的关系，因此，局部方法无法达到“使在数据流形上相距较远的样本的特征也相距较远”的目的。

以下是对一组三维数据（900样本）降到一维，应用八种算法的时间对比：