Computing Normals

Terrain Tutorial

Computing Normals

To apply lighting to a terrain, either using OpenGL lights, or simulating them, it is necessary to first compute normals. A normal is a vector that defines how a surface responds to lighting, i.e. how it is lit. The amount of light reflected by a surface is proportional to the angle between the lights direction and the normal. The smaller the angle the brighter the surface will look.

Normals in OpenGL can be defined per face or per vertex. If defining a normal per face then the normal is commonly defined as a vector which is perpendicular to the surface. In order to find a perpendicular vector to a face, two vectors coplanar with the face are needed. Afterwards the cross product will provide the normal vector, i.e. a perpendicular vector to the face.

So the first step is to compute two vectors coplanar to a face. Assuming the the faces are triangles defined by points t1,t2,t3, then two possible vectors are:

v1 = t2 - t1

v2 = t3 - t1

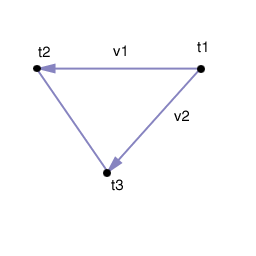With the two vectors, v1 and v2, it is now possible to compute the cross product between them to find a perpendicular vector to the face.

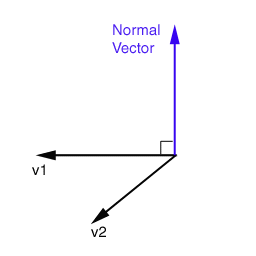The equations bellow show the necessary steps to compute a normal vector v. The required opeartion is called cross product, and it is represented by "x".

    
	v = v1 x v2
	
	v = [vx,vy,vz] where,
	
		vx = v1y * v2z - v1z * v2y
		
		vy = v1z * v2x - v1x * v2z
		
		vz = v1x * v2y - v1y * v2x

Another necessary step to obtain proper lighting is to normalise the vector, i.e. make it unit length. OpenGL takes into consideration the length of the normal vector when computing lighting. Normalisation implies first computing the lenght of the vector, and then dividing each component by the vectors length.

The length of a vector is computed as:

Therefore the normalized vector nv is computed as:

    
	nv = [nvx,nvy,nvz] where,
	
		nvx = vx / l
		nvy = vy / l
		nvz = vz / l

The main problem with assigning a normal per face is that the terrain looks faceted, i.e. the brightness of each face is constant, and there is a clear difference between faces with differen orientations. In order to get a smoother look normals should be computed per vertex, and not per face. When computing normals per vertex it is necessary to take into account the faces that share the vertex. So for instance if using quads, each vertex (excluding the corner and border vertices), is shared by four polygons. The normal at a vertex should be computed as the normalised sum of all the unit length normals for each face the vertex shares. Consider the following image:

In the above image, v represents the normal at the center vertex. Each vij represents a normal for each face that shares the center vertex. So for instance v12 is the unit lenght normal for the bottom right face.

The vertex normal v is computed as the normalised sum of all vij vectors:

    
	v = normalised(sum(v12, v23, v34, v41))
	
	where
	
		vij = normalised(vi x vj) // normalised cross product

It is also posible to consider the eight neighbour vertices, instead of only four. This latter option will probably look smoother in the general case.