利用多核多线程进行程序优化
1.样例程序
程序功能:求从1一直到 APPLE_MAX_VALUE (100000000) 相加累计的和,并赋值给 apple 的 a 和 b ;求 orange 数据结构中的 a[i]+b[i ] 的和,循环 ORANGE_MAX_VALUE (1000000) 次。说明:
(1)由于样例程序是从实际应用中抽象出来的模型,所以本文不会进行 test.a=test.b= test.b+sum 、中间变量(查找表)等类似的优化。
(2)以下所有程序片断均为部分代码,完整代码请参看本文最下面的附件。
清单 1. 样例程序
#define ORANGE_MAX_VALUE 1000000
#define APPLE_MAX_VALUE 100000000
#define MSECOND 1000000
struct apple
{
unsigned long long a;
unsigned long long b;
};
struct orange
{
int a[ORANGE_MAX_VALUE];
int b[ORANGE_MAX_VALUE];
};
int main (int argc, const char * argv[]) {
// insert code here...
struct apple test;
struct orange test1;
for(sum=0;sum<APPLE_MAX_VALUE;sum++)
{
test.a += sum;
test.b += sum;
}
sum=0;
for(index=0;index<ORANGE_MAX_VALUE;index++)
{
sum += test1.a[index]+test1.b[index];
}
return 0;
}
2. K-Best 测量方法
在检测程序运行时间这个复杂问题上,将采用 Randal E.Bryant 和 David R. O’Hallaron 提出的 K 次最优测量方法。假设重复的执行一个程序,并纪录 K 次最快的时间,如果发现测量的误差 ε 很小,那么用测量的最快值表示过程的真正执行时间, 称这种方法为“ K 次最优(K-Best)方法”,要求设置三个参数:
K: 要求在某个接近最快值范围内的测量值数量。按照升序的方式维护一个 K 个最快时间的数组,对于每一个新的测量值,如果比当前 K 处的值更快,则用最新的值替换数组中的元素 K ,然后再进行升序排序,持续不断的进行该过程,并满足误差标准,此时就称测量值已经收敛。如果 M 次后,不能满足误差标准,则称为不能收敛。
ε 测量值必须多大程度的接近,即测量值按照升序标号 V1, V2, V3, … , Vi, … ,同时必须满足(1+ ε)Vi >= Vk
M: 在结束测试之前,测量值的最大数量。
在接下来的所有试验中,采用 K=10,ε=2%,M=200 来获取程序运行时间,同时也对 K 次最优测量方法进行了改进,不是采用最小值来表示程序执行的时间,而是采用 K 次测量值的平均值来表示程序的真正运行时间。由于采用的误差 ε 比较大,在所有试验程序的时间收集过程中,均能收敛,但也能说明问题。
为了可移植性,采用 gettimeofday() 来获取系统时钟(system clock)时间,可以精确到微秒。
3. 测试环境
硬件:联想 Dual-core 双核机器,主频 2.4G,内存 2G
软件:Suse Linunx Enterprise 10,内核版本:linux-2.6.16
4. 软件优化的三个层次
医生治病首先要望闻问切,然后才确定病因,最后再对症下药,如果胡乱医治一通,不死也残废。说起来大家都懂的道理,但在软件优化过程中,往往都喜欢犯这样的错误。不分青红皂白,一上来这里改改,那里改改,其结果往往不如人意。
一般将软件优化可分为三个层次:系统层面,应用层面及微架构层面。首先从宏观进行考虑,进行望闻问切,即系统层面的优化,把所有与程序相关的信息收集上来,确定病因。确定病因后,开始从微观上进行优化,即进行应用层面和微架构方面的优化。
系统层面的优化:内存不够,CPU 速度过慢,系统中进程过多等
应用层面的优化:算法优化、并行设计等
微架构层面的优化:分支预测、数据结构优化、指令优化等
软件优化可以在应用开发的任一阶段进行,当然越早越好,这样以后的麻烦就会少很多。
在实际应用程序中,采用最多的是应用层面的优化,也会采用微架构层面的优化。将某些优化和维护成本进行对比,往往选择的都是后者。如分支预测优化和指令优化,在大型应用程序中,往往采用的比较少,因为维护成本过高。
本文将从应用层面和微架构层面,对样例程序进行优化。对于应用层面的优化,将采用多线程和 CPU 亲和力技术;在微架构层面,采用 Cache 优化。
5. 并行设计
利用并行程序设计模型来设计应用程序,就必须把自己的思维从线性模型中拉出来,重新审视整个处理流程,从头到尾梳理一遍,将能够并行执行的部分识别出来。
可以将应用程序看成是众多相互依赖的任务的集合。将应用程序划分成多个独立的任务,并确定这些任务之间的相互依赖关系,这个过程被称为分解(Decomosition)。分解问题的方式主要有三种:任务分解、数据分解和数据流分解。关于这部分的详细资料,请参看参考资料一。
仔细分析样例程序,运用任务分解的方法 ,不难发现计算 apple 的值和计算 orange 的值,属于完全不相关的两个操作,因此可以并行。
改造后的两线程程序:
清单 2. 两线程程序
void* add(void* x)
{
for(sum=0;sum<APPLE_MAX_VALUE;sum++)
{
((struct apple *)x)->a += sum;
((struct apple *)x)->b += sum;
}
return NULL;
}
int main (int argc, const char * argv[]) {
// insert code here...
struct apple test;
struct orange test1={{0},{0}};
pthread_t ThreadA;
pthread_create(&ThreadA,NULL,add,&test);
for(index=0;index<ORANGE_MAX_VALUE;index++)
{
sum += test1.a[index]+test1.b[index];
}
pthread_join(ThreadA,NULL);
return 0;
}
更甚一步,通过数据分解的方法,还可以发现,计算 apple 的值可以分解为两个线程,一个用于计算 apple a 的值,另外一个线程用于计算 apple b 的值(说明:本方案抽象于实际的应用程序)。但两个线程存在同时访问 apple 的可能性,所以需要加锁访问该数据结构。
改造后的三线程程序如下:
清单 3. 三线程程序
struct apple
{
unsigned long long a;
unsigned long long b;
pthread_rwlock_t rwLock;
};
void* addx(void* x)
{
pthread_rwlock_wrlock(&((struct apple *)x)->rwLock);
for(sum=0;sum<APPLE_MAX_VALUE;sum++)
{
((struct apple *)x)->a += sum;
}
pthread_rwlock_unlock(&((struct apple *)x)->rwLock);
return NULL;
}
void* addy(void* y)
{
pthread_rwlock_wrlock(&((struct apple *)y)->rwLock);
for(sum=0;sum<APPLE_MAX_VALUE;sum++)
{
((struct apple *)y)->b += sum;
}
pthread_rwlock_unlock(&((struct apple *)y)->rwLock);
return NULL;
}
int main (int argc, const char * argv[]) {
// insert code here...
struct apple test;
struct orange test1={{0},{0}};
pthread_t ThreadA,ThreadB;
pthread_create(&ThreadA,NULL,addx,&test);
pthread_create(&ThreadB,NULL,addy,&test);
for(index=0;index<ORANGE_MAX_VALUE;index++)
{
sum+=test1.a[index]+test1.b[index];
}
pthread_join(ThreadA,NULL);
pthread_join(ThreadB,NULL);
return 0;
}
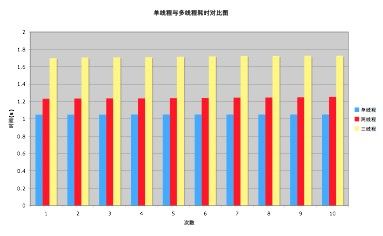
这样改造后,真的能达到我们想要的效果吗?通过 K-Best 测量方法,其结果让我们大失所望,如下图:
图 1. 单线程与多线程耗时对比图
为什么多线程会比单线程更耗时呢?其原因就在于,线程启停以及线程上下文切换都会引起额外的开销,所以消耗的时间比单线程多。
为什么加锁后的三线程比两线程还慢呢?其原因也很简单,那把读写锁就是罪魁祸首。通过 Thread Viewer 也可以印证刚才的结果,实际情况并不是并行执行,反而成了串行执行,如图2:
其中最下面那个线程是主线程,一个是 addx 线程,另外一个是 addy 线程,从图中不难看出,其他两个线程为串行执行。
通过数据分解来划分多线程,还存在另外一种方式,一个线程计算从1到 APPLE_MAX_VALUE/2 的值,另外一个线程计算从 APPLE_MAX_VALUE/2+1 到 APPLE_MAX_VALUE 的值,但本文会弃用这种模型,有兴趣的读者可以试一试。
在采用多线程方法设计程序时,如果产生的额外开销大于线程的工作任务,就没有并行的必要。线程并不是越多越好,软件线程的数量尽量能与硬件线程的数量相匹配。最好根据实际的需要,通过不断的调优,来确定线程数量的最佳值。
6. 加锁与不加锁
针对加锁的三线程方案,由于两个线程访问的是 apple 的不同元素,根本没有加锁的必要,所以修改 apple 的数据结构(删除读写锁代码),通过不加锁来提高性能。
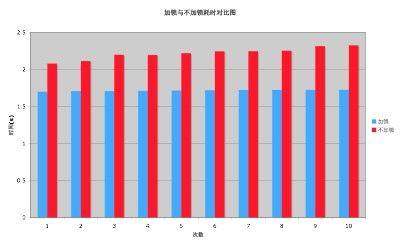
测试结果如下:
其结果再一次大跌眼镜,可能有些人就会越来越糊涂了,怎么不加锁的效率反而更低呢?将在针对 Cache 的优化一节中细细分析其具体原因。
在实际测试过程中,不加锁的三线程方案非常不稳定,有时所花费的时间相差4倍多。
要提高并行程序的性能,在设计时就需要在较少同步和较多同步之间寻求折中。同步太少会导致错误的结果,同步太多又会导致效率过低。尽量使用私有锁,降低锁的粒度。无锁设计既有优点也有缺点,无锁方案能充分提高效率,但使得设计更加复杂,维护操作困难,不得不借助其他机制来保证程序的正确性。
7. 针对 Cache 的优化
在串行程序设计过程中,为了节约带宽或者存储空间,比较直接的方法,就是对数据结构做一些针对性的设计,将数据压缩 (pack) 的更紧凑,减少数据的移动,以此来提高程序的性能。但在多核多线程程序中,这种方法往往有时会适得其反。
数据不仅在执行核和存储器之间移动,还会在执行核之间传输。根据数据相关性,其中有两种读写模式会涉及到数据的移动:写后读和写后写 ,因为这两种模式会引发数据的竞争,表面上是并行执行,但实际只能串行执行,进而影响到性能。
处理器交换的最小单元是 cache 行,或称 cache 块。在多核体系中,对于不共享 cache 的架构来说,两个独立的 cache 在需要读取同一 cache 行时,会共享该 cache 行,如果在其中一个 cache 中,该 cache 行被写入,而在另一个 cache 中该 cache 行被读取,那么即使读写的地址不相交,也需要在这两个 cache 之间移动数据,这就被称为 cache 伪共享,导致执行核必须在存储总线上来回传递这个 cache 行,这种现象被称为“乒乓效应”。
同样地,当两个线程写入同一个 cache 的不同部分时,也会互相竞争该 cache 行,也就是写后写的问题。上文曾提到,不加锁的方案反而比加锁的方案更慢,就是互相竞争 cache 的原因。
在 X86 机器上,某些处理器的一个 cache 行是64字节,具体可以参看 Intel 的参考手册。
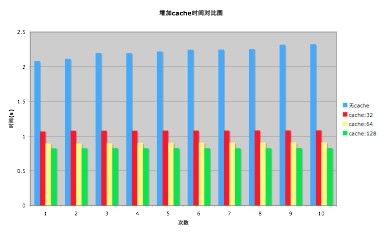
既然不加锁三线程方案的瓶颈在于 cache,那么让 apple 的两个成员 a 和 b 位于不同的 cache 行中,效率会有所提高吗?
修改后的代码片断如下:
struct apple
{
unsigned long long a;
char c[128]; /*32,64,128*/
unsigned long long b;
};
小小的一行代码,尽然带来了如此高的收益,不难看出,我们是用空间来换时间。当然读者也可以采用更简便的方法: __attribute__((__aligned__(L1_CACHE_BYTES))) 来确定 cache 的大小。
如果对加锁三线程方案中的 apple 数据结构也增加一行类似功能的代码,效率也是否会提升呢?性能不会有所提升,其原因是加锁的三线程方案效率低下的原因不是 Cache 失效造成的,而是那把锁。
在多核和多线程程序设计过程中,要全盘考虑多个线程的访存需求,不要单独考虑一个线程的需求。在选择并行任务分解方法时,要综合考虑访存带宽和竞争问题,将不同处理器和不同线程使用的数据放在不同的 Cache 行中,将只读数据和可写数据分离开。
8. CPU 亲和力
CPU 亲和力可分为两大类:软亲和力和硬亲和力。
Linux 内核进程调度器天生就具有被称为 CPU 软亲和力(affinity) 的特性,这意味着进程通常不会在处理器之间频繁迁移。这种状态正是我们希望的,因为进程迁移的频率小就意味着产生的负载小。但不代表不会进行小范围的迁移。
CPU 硬亲和力是指进程固定在某个处理器上运行,而不是在不同的处理器之间进行频繁的迁移。这样不仅改善了程序的性能,还提高了程序的可靠性。
从以上不难看出,在某种程度上硬亲和力比软亲和力具有一定的优势。但在内核开发者不断的努力下,2.6内核软亲和力的缺陷已经比2.4的内核有了很大的改善。
在双核机器上,针对两线程的方案,如果将计算 apple 的线程绑定到一个 CPU 上,将计算 orange 的线程绑定到另外一个 CPU 上,效率是否会有所提高呢?
程序如下:
struct apple
{
unsigned long long a;
unsigned long long b;
};
struct orange
{
int a[ORANGE_MAX_VALUE];
int b[ORANGE_MAX_VALUE];
};
inline int set_cpu(int i)
{
CPU_ZERO(&mask);
if(2 <= cpu_nums)
{
CPU_SET(i,&mask);
if(-1 == sched_setaffinity(gettid(),sizeof(&mask),&mask))
{
return -1;
}
}
return 0;
}
void* add(void* x)
{
if(-1 == set_cpu(1))
{
return NULL;
}
for(sum=0;sum<APPLE_MAX_VALUE;sum++)
{
((struct apple *)x)->a += sum;
((struct apple *)x)->b += sum;
}
return NULL;
}
int main (int argc, const char * argv[]) {
// insert code here...
struct apple test;
struct orange test1;
cpu_nums = sysconf(_SC_NPROCESSORS_CONF);
if(-1 == set_cpu(0))
{
return -1;
}
pthread_create(&ThreadA,NULL,add,&test);
for(index=0;index<ORANGE_MAX_VALUE;index++)
{
sum+=test1.a[index]+test1.b[index];
}
pthread_join(ThreadA,NULL);
return 0;
}
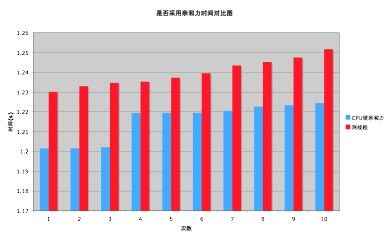
测量结果为:
其测量结果正是我们所希望的,但花费的时间还是比单线程的多,其原因与上面分析的类似。
进一步分析不难发现,样例程序大部分时间都消耗在计算 apple 上,如果将计算 a 和 b 的值,分布到不同的 CPU 上进行计算,同时考虑 Cache 的影响,效率是否也会有所提升呢?
从时间上观察,设置亲和力的程序所花费的时间略高于采用 Cache 的三线程方案。由于考虑了 Cache 的影响,排除了一级缓存造成的瓶颈,多出的时间主要消耗在系统调用及内核上,可以通过 time 命令来验证:
#time ./unlockcachemultiprocess
real 0m0.834s user 0m1.644s sys 0m0.004s
#time ./affinityunlockcacheprocess
real 0m0.875s user 0m1.716s sys 0m0.008s
|
通过设置 CPU 亲和力来利用多核特性,为提高应用程序性能提供了捷径。同时也是一把双刃剑,如果忽略负载均衡、数据竞争等因素,效率将大打折扣,甚至带来事倍功半的结果。
在进行具体的设计过程中,需要设计良好的数据结构和算法,使其适合于应用的数据移动和处理器的性能特性。
9. 总结
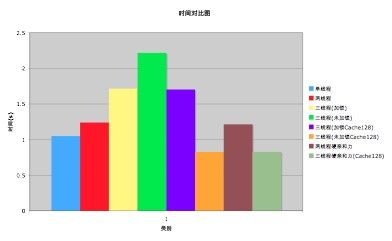
根据以上分析及实验,对所有改进方案的测试时间做一个综合对比,如下图所示:
单线程原始程序平均耗时:1.049046s,最慢的不加锁三线程方案平均耗时:2.217413s,最快的三线程( Cache 为128)平均耗时:0.826674s,效率提升约26%。当然,还可以进一步优化,让效率得到更高的提升。
从上图不难得出结论:采用多核多线程并行设计方案,能有效提高性能,但如果考虑不全面,如忽略带宽、数据竞争及数据同步不当等因素,效率反而降低,程序执行越来越慢。
如果抛开本文开篇时的限制,采用上文曾提到的另外一种数据分解模型,同时结合硬亲和力对样例程序进行优化,测试时间为0.54s,效率提升了92%。
软件优化是一个贯穿整个软件开发周期,从开始设计到最终完成一直进行的连续过程。在优化前,需要找出瓶颈和热点所在。正如最伟大的 C 语言大师 Rob Pike 所说:
如果你无法断定程序会在什么地方耗费运行时间,瓶颈经常出现在意想不到的地方,所以别急于胡乱找个地方改代码,除非你已经证实那儿就是瓶颈所在。
将这句话送给所有的优化人员,和大家共勉。
10 参考资料
- 请参考书籍《多核程序设计技术》,了解更多关于多线程设计的理念
- 请参考书籍《软件优化技术》,了解更多关于软件优化的技术
- 请参考书籍《UNIX编程艺术》, 了解更多关于软件架构方面的知识
- 参考文章《CPU Affinity》,了解更多关于CPU亲和力的信息
- 参考文章《管理处理器的亲和性(affinity)》,了解更多关于CPU亲和力的信息