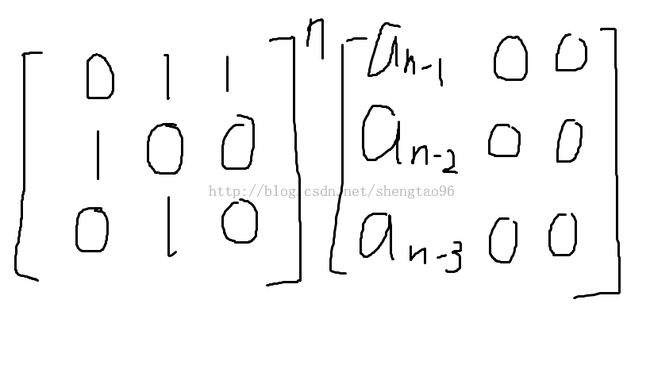acm.dlut.edu.cn--1326--FFFFFF--（矩阵快速幂）

1326: FFFFFF

Time Limit: 1 Sec   Memory Limit: 128 MB
Submit: 111   Solved: 33
[ Submit][ Status][ Web Board]

Description

光教练得到了n个不同的数（不要在意是哪些数），光教练决定按照以下规定选取若干个数：

1.若选取第i个数，则不能选取第i+1个数

2.编号连续的3个数（i-1,i,i+1）中，至少有一个必须被选取

光教练想知道，按以上的选区方案，最多有多少种方案数？

Input

一行，一个整数n(n<=10^18)

Output

一行，方案数，结果模(10^9+7) 

Sample Input

129

Sample Output

2321

HINT

对于第一组样例，一个数，可以选或者不选，算两种

链接：http://acm.dlut.edu.cn/problem.php?id=1326

思路：先找规律把，a1=2，a2=3，a3=4，a4=5，a5=7，a6=9，a7=12，a8=16，a9=21，a10=28.......

            根据数列增加的规律，易知a（n）=a（n-2）+a（n-3）

           考虑矩阵快速幂，矩阵如下：

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cmath>
#include <stack>
#include <vector>
#include <map>
#define maxn 3
#define mem(a,b)  memset(a,b,sizeof(a))
using namespace std;
typedef long long ll;
const int mod=1000000000+7;
struct matrix
{
    int n;
    ll maze[maxn][maxn];
    void init(int n)
    {
        this->n=n;
        mem(maze,0);
    }
    matrix operator *(matrix& rhs)
    {
        matrix ans;
        ans.init(3);
        for(int i=0; i<n; i++)
        for(int j=0; j<n; j++)
        for(int k=0; k<n; k++)
        {
            ans.maze[i][j]=(ans.maze[i][j]+maze[i][k]*rhs.maze[k][j])%mod;
        }
        return ans;
    }
} a,ans;
void qpow(ll n)
{
    a.init(3);
    a.maze[0][1]=a.maze[0][2]=a.maze[1][0]=a.maze[2][1]=1;
    ans.init(3);
    ans.maze[0][0]=ans.maze[1][1]=ans.maze[2][2]=1;
    while(n)
    {
        if(n&1)ans=ans*a;
        a=a*a;
        n>>=1;
    }
}
int main()
{
    ll n;
    while(cin>>n)
    {
        qpow(n);
        cout<<(ans.maze[0][0]*2+ans.maze[0][1]+ans.maze[0][2])%mod<<endl;
    }
    return 0;
}

复制去Google翻译 翻译结果