ML—决策树(train,matlab)
华电北风吹
天津大学认知计算与应用重点实验室
修改日期:2015/8/11
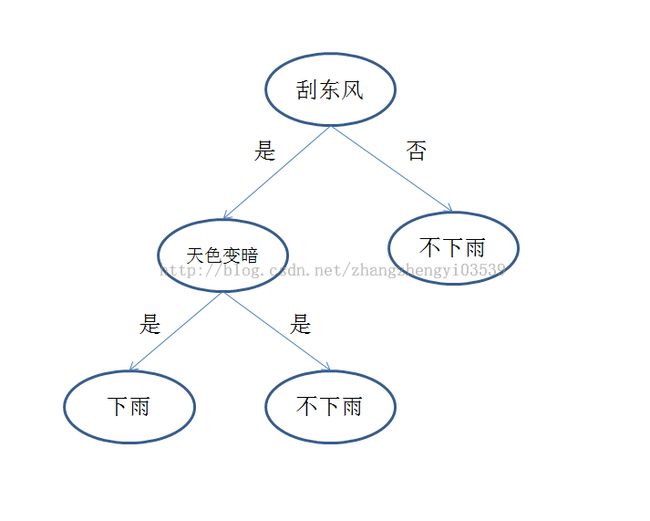
决策树是一种特别简单的机器学习分类算法。决策树想法来源于人类的决策过程。举个最简单的例子,人类发现下雨的时候,往往会有刮东风,然后天色变暗。对应于决策树模型,预测天气模型中的刮东风和天色变暗就是我们收集的特征,是否下雨就是类别标签。构建的决策树如下图所示
决策树模型构建过程为,在特征集合中无放回的依次递归抽选特征作为决策树的节点——当前节点信息增益或者增益率最大,当前节点的值作为当前节点分支出来的有向边(实际上主要选择的是这些边,这个由信息增益的计算公式就可以得到)。对于这个进行直观解释
来说一个极端情况,如果有一个特征下,特征取不同值的时候,对应的类别标签都是纯的,决策者肯定会选择这个特征,作为鉴别未知数据的判别准则。由下面的计算信息增益的公式可以发现这时候对应的信息增益是最大的。
g(D,A)=H(D)-H(D|A)
g(D,A):表示特征A对训练数据集D的信息增益
H(D):表示数据集合D的经验熵
H(D|A):表示特征A给定条件下数据集合D的条件熵。
反之,当某个特征它的各个取值下对应的类别标签均匀分布的时候H(D|A)最大,又对于所有的特征H(D)是都一样的。因此,这时候的g(D,A)最小。
总之一句话,我们要挑选的特征是:当前特征下各个取值包含的分类信息最明确。
下面我们来看一个MATLAB编写的决策树算法,帮助理解
树终止条件为
1、特征数为空
2、树为纯的
3、信息增益或增益率小于阀值
主函数:
clear;clc;
% OutlookType=struct('Sunny',1,'Rainy',2,'Overcast',3);
% TemperatureType=struct('hot',1,'warm',2,'cool',3);
% HumidityType=struct('high',1,'norm',2);
% WindyType={'True',1,'False',0};
% PlayGolf={'Yes',1,'No',0};
% data=struct('Outlook',[],'Temperature',[],'Humidity',[],'Windy',[],'PlayGolf',[]);
Outlook=[1,1,3,2,2,2,3,1,1,2,1,3,3,2]';
Temperature=[1,1,1,2,3,3,3,2,3,3,2,2,1,2]';
Humidity=[1,1,1,1,2,2,2,1,2,2,2,1,2,1]';
Windy=[0,1,0,0,0,1,1,0,0,0,1,1,0,1]';
data=[Outlook Temperature Humidity Windy];
PlayGolf=[0,0,1,1,1,0,1,0,1,1,1,1,1,0]';
propertyName={'Outlook','Temperature','Humidity','Windy'};
delta=0.1;
decisionTreeModel=decisionTree(data,PlayGolf,propertyName,delta);
构建模型主函数部分
function decisionTreeModel=decisionTree(data,label,propertyName,delta)
global Node;
Node=struct('fatherNodeName',[],'EdgeProperty',[],'NodeName',[]);
BuildTree('root','Stem',data,label,propertyName,delta);
Node(1)=[];
model.Node=Node;
decisionTreeModel=model;
递归构建树
function BuildTree(fatherNodeName,edge,data,label,propertyName,delta)
global Node;
sonNode=struct('fatherNodeName',[],'EdgeProperty',[],'NodeName',[]);
sonNode.fatherNodeName=fatherNodeName;
sonNode.EdgeProperty=edge;
if length(unique(label))==1
sonNode.NodeName=label(1);
Node=[Node sonNode];
return;
end
if length(propertyName)<1
labelSet=unique(label);
k=length(labelSet);
labelNum=zeros(k,1);
for i=1:k
labelNum(i)=length(find(label==labelSet(i)));
end
[~,labelIndex]=max(labelNum);
sonNode.NodeName=labelSet(labelIndex);
Node=[Node sonNode];
return;
end
[sonIndex,BuildNode]=CalcuteNode(data,label,delta);
if BuildNode
dataRowIndex=setdiff(1:length(propertyName),sonIndex);
sonNode.NodeName=propertyName{sonIndex};
Node=[Node sonNode];
propertyName(sonIndex)=[];
sonData=data(:,sonIndex);
sonEdge=unique(sonData);
for i=1:length(sonEdge)
edgeDataIndex=find(sonData==sonEdge(i));
BuildTree(sonNode.NodeName,sonEdge(i),data(edgeDataIndex,dataRowIndex),label(edgeDataIndex,:),propertyName,delta);
end
else
labelSet=unique(label);
k=length(labelSet);
labelNum=zeros(k,1);
for i=1:k
labelNum(i)=length(find(label==labelSet(i)));
end
[~,labelIndex]=max(labelNum);
sonNode.NodeName=labelSet(labelIndex);
Node=[Node sonNode];
return;
end
计算下一个树节点的特征
function [NodeIndex,BuildNode]=CalcuteNode(data,label,delta)
LargeEntropy=CEntropy(label);
[m,n]=size(data);
EntropyGain=LargeEntropy*ones(1,n);
BuildNode=true;
for i=1:n
pData=data(:,i);
itemList=unique(pData);
for j=1:length(itemList)
itemIndex=find(pData==itemList(j));
EntropyGain(i)=EntropyGain(i)-length(itemIndex)/m*CEntropy(label(itemIndex));
end
% 此处运行则为增益率,注释掉则为增益
% EntropyGain(i)=EntropyGain(i)/CEntropy(pData);
end
[maxGainEntropy,NodeIndex]=max(EntropyGain);
if maxGainEntropy<delta
BuildNode=false;
end
计算熵
function result=CEntropy(propertyList)
result=0;
totalLength=length(propertyList);
itemList=unique(propertyList);
pNum=length(itemList);
for i=1:pNum
itemLength=length(find(propertyList==itemList(i)));
pItem=itemLength/totalLength;
result=result-pItem*log2(pItem);
end
输出的数据结构是Node类型的,
struct('fatherNodeName',[],'EdgeProperty',[],'NodeName',[])因为MATLAB没有面向对象的功能,如果用python,java,C#的时候,写个二叉树会更方便。