小波工具箱使用3
一维离散平稳小波分析
离散平稳小波分析所用到的函数有swt小波分解和iswt小波重构。在这一部分可以学到如下内容:
l 加载信号
l 执行平稳小波分解
l 从小波系数中构造近似和细节
l 显示第一层的近似和细节
l 平稳小波逆变换恢复原始信号
l 执行多层平稳小波分解
l 重构第3层近似
l 重构1、2、3层细节
l 重构1、2层近似
l 显示分解的结果
l 从3层分解中重构原始信号
l 除噪
使用命令行实现一维分析
1. 加载信号(一个噪声污染的多普勒效应信号)
2. 设置变量
s = noisdopp;
对于SWT变换,如果需要在第k层分解信号,那么原始信号需要能够平分成2^k份。所以如果原始信号的长度不满足要求,需要使用Signal Extension GUI工具或使用wextend函数来扩展它。
3. 执行一层平稳小波分解
[swa,swd] = swt(s,1,'db1');
函数执行将产生1层近似和细节的系数,两者和信号的长度是相等的,这也是平稳小波和普通小波不同的地方,从而使它在某些领域有好的效果。
4. 显示近似、细节小波系数
显示一层近似和细节的系数
subplot(1,2,1), plot(swa); title('Approximation cfs')
subplot(1,2,2), plot(swd); title('Detail cfs')
5. 使用平稳小波逆变换恢复原始信号
A0 = iswt(swa,swd,'db1');
重构的误差为
err = norm(s-A0)
err =
2.1450e-014
6. 从系数中构建近似和细节
构建一层近似和细节,输入如下代码
nulcfs = zeros(size(swa));
A1 = iswt(swa,nulcfs,'db1');
D1 = iswt(nulcfs,swd,'db1');
显示结果如下
subplot(1,2,1), plot(A1); title('Approximation A1');
subplot(1,2,2), plot(D1); title('Detail D1');
7. 执行多层平稳小波分解
使用db1小波做3层小波分解
[swa,swd] = swt(s,3,'db1');
产生的近似系数在swa中,细节系数在swd中,而且它们有相同的长度。
8. 显示近似和细节的系数
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(swa(i,:));
title(['Approx. cfs level ',num2str(i)])
subplot(3,2,kp+2), plot(swd(i,:));
title(['Detail cfs level ',num2str(i)])
kp = kp + 2;
end
9. 从系数中重建第3层的近似
mzero = zeros(size(swd));
A = mzero;
A(3,:) = iswt(swa,mzero,'db1');
10. 从系数中重建细节
D = mzero;
for i = 1:3
swcfs = mzero;
swcfs(i,:) = swd(i,:);
D(i,:) = iswt(mzero,swcfs,'db1');
End
11. 从第3层近似和第2、3层细节中重建第1、2层近似
重建2、3层的近似
A(2,:) = A(3,:) + D(3,:);
A(1,:) = A(2,:) + D(2,:);
显示第1、2、3层的近似和细节
kp = 0;
for i = 1:3
subplot(3,2,kp+1), plot(A(i,:));
title(['Approx. level ',num2str(i)])
subplot(3,2,kp+2), plot(D(i,:));
title(['Detail level ',num2str(i)])
kp = kp + 2;
end
12. 阈值除噪
要去除噪声,先使用ddencmp函数计算一个默认的全局阈值,再使用wthresh函数执行细节系数的实际阈值,然后使用iswt得到除噪信号。
所有在一维离散小波变换中选择阈值的方法在一维平稳小波变换中都是有效的,GUI中两者的使用方法也一样。
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
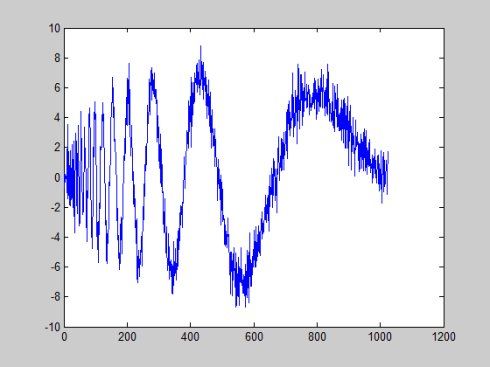
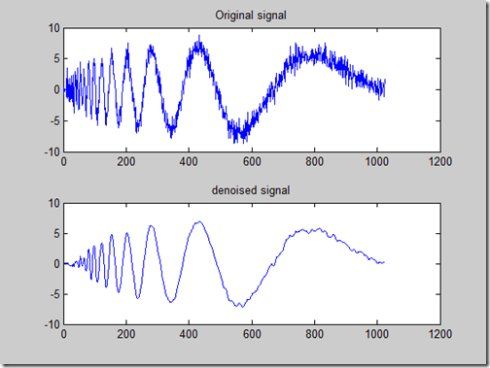
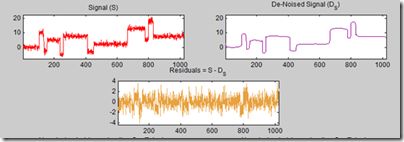
显示原始信号和除噪信号如下
subplot(2,1,1), plot(s);
title('Original signal')
subplot(2,1,2), plot(clean);
title('denoised signal')
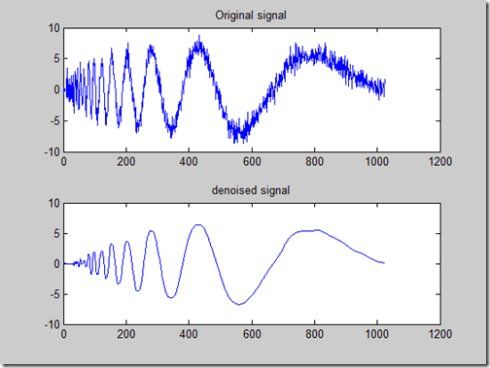
得到的信号仍然有一些噪声,结果可以通过考虑对信号进行5层分解,然后再除噪来改善,如下
[swa,swd] = swt(s,5,'db1');
[thr,sorh] = ddencmp('den','wv',s);
dswd = wthresh(swd,sorh,thr);
clean = iswt(swa,dswd,'db1');
subplot(2,1,1), plot(s); title('Original signal')
subplot(2,1,2), plot(clean); title('denoised signal')
第二种实现相同效果的语法如下
lev = 5; swc = swt(s,lev,'db1');
swcden = swc;
swcden(1:end-1,:) = wthresh(swcden(1:end-1,:),sorh,thr);
clean = iswt(swcden,'db1');
使用图形接口做一维除噪分析
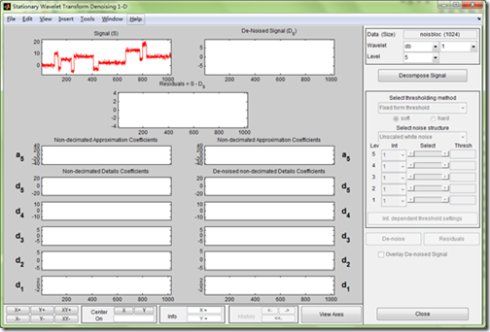
1. 开启一维平稳小波除噪工具
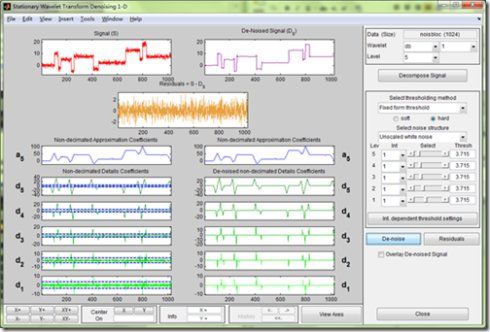
输入wavemenu,选择SWT Denoising 1-D,出现如下GUI
2. 加载信号
Load Signal
3. 执行平稳小波分解
使用db1小波执行5层小波分解,得到的是非抽取系数(nondecimated coefficients),它们是使用相同的离散小波变换来得到的,只是省略了抽取的步骤。得到的结果如下
4. 使用平稳小波变换除噪
可以使用GUI默认的参数做除噪处理。右边的滑动条可以控制各级系数的阈值大小,也可以直接在系数图中直接拖动来调整阈值的大小,注意近似系数中没有阈值。点击denoise进行除噪处理
得到的效果是非常好的,但似乎在信号不连续的地方出现了过平滑,这个可以从残差图中看出来,在800的位置出现了突降点。
选择hard阈值模式代替soft模式,再进行除噪,结果如下
可以看到这次效果非常好,而且残差图也看起来像白噪声序列。为了验证这一点,可以点击Residuals按钮查看残差图及相关统计数据来详细说明。