MFC 实现 加减乘除，括号，乘方的 计算器

MFC 实现  可加减乘除，括号，乘方 以及进制转换的 计算器

一、带括号的四则运算以及乘方运算

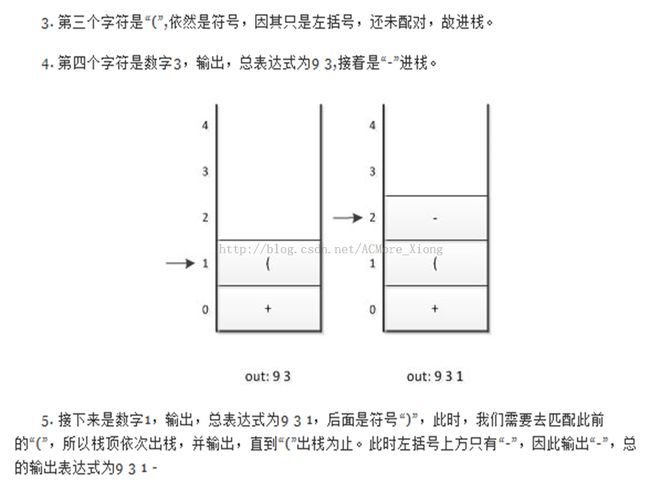
输入的字符串为中缀表达式，我们对表达式进行求值，则首先要解决的问题即为运算优先级，然后再进行求值，通俗的说就是我先根据计算优先级确定好表达式计算的顺序，然后我在根据这个顺序一步一步进行计算。。

那么，首先，我们先处理运算优先级，这里我们用到数据结构以及离散数学里面的一个知识点，将中缀表达式转化为后（前）缀表达式，或者说是将中序遍历表达式树转化为后（前）序遍历。这里 小熊 给大家介绍的方法是 中缀表达式转化为后缀表达式。

学过了数据结构的同学这里应该很容易理解，比如表达式a*(b+ c)-d我们这里转化的规则为：

从左到右扫描a*(b + c)-d的每一数字和符号，若是数字就输出，即成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘方优先乘除，乘除优先加减）则栈顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止。【PS：这里“输出”的意思是将字符存入 一个字符串里面】。

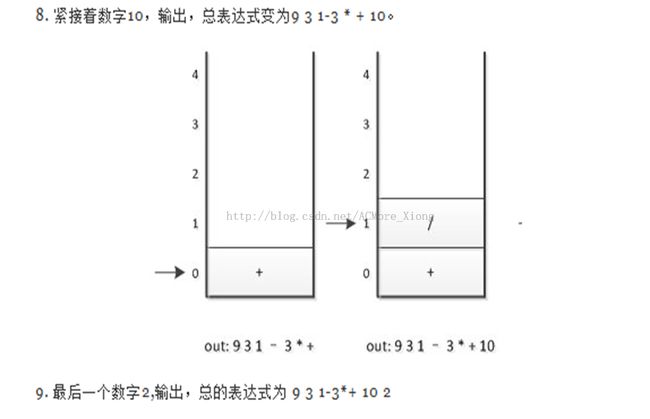
考虑到读者可能还是感到有点迷惑，小熊 以具体的例子给大家进行分析吧！比如，输入的表示式为9+(3-1)*3+10/2【这样运算符号在两数字之间的，叫做中缀表达式】

【PS：下图非原创，为了大家能够清楚地理解这个过程，引用了别人的例子】

相信看完这个例子，大家应该都理解这个过程了！下面给出相应的源码

预备工作：

#include  “stack”

#include “math.h”

using namespace std；

const char lNumFront = '[';//两个数字之间的分隔符

const char rNumBack = ']';//两个数字之间的分隔符

const CString LPCT_OPCH = "+-*/^";//保存运算符

INT CCalculatorDlg::PriorityLevel(char op)
{
 if(op=='+'||op=='-')
        return 1;
    if(op=='*'||op=='/')
        return 2;
    if(op=='^')
        return 3;
    return 0;
}
BOOL CCalculatorDlg::IsOpr(char c)
{
 for(int i = 0;i < LPCT_OPCH.GetLength();i++){
        if(c==LPCT_OPCH[i]) return true;
    }
    return false;
}

//中缀转为后缀
CString CCalculatorDlg::InfixToSuffix(CString szIn)
{
 CString ans = "";
    stack<char>Optr;
    for(int i = 0; i < szIn.GetLength(); i++) {
        char c = szIn[i];
        if(c>='0'&&c<='9') //数字直接输出
  {
            ans+=lNumFront;
            ans+=c;
            while(i+1<szIn.GetLength()&&szIn[i+1]>='0'&&szIn[i+1]<='9') {
    ans+=szIn[i+1]; ++i;
   }
            ans += rNumBack;
        }
  else if(Optr.empty()) 
  {
            Optr.push(c);
        }
  else if(c=='(') //无条件压栈
  {
            Optr.push(c);
        }
  else if(c==')')  //弹栈并输出
  {
            while(Optr.top()!='(') 
   {
                if(Optr.empty()) //基于安全性的考虑
    {
     AfxMessageBox("提示:括号不匹配！");
     ASSERT(Optr.empty());
                    //return ans;
                }
                ans+=Optr.top();
                Optr.pop();
            }
            Optr.pop();
        } 
  else//其他条件即为 + - * / ^
  {
            if(PriorityLevel(c) > PriorityLevel(Optr.top()))
                Optr.push(c);
            else 
   {
                while(!Optr.empty()&&PriorityLevel(c) <= PriorityLevel(Optr.top()))
    {
                    ans+=Optr.top();
                    Optr.pop();
                }
                Optr.push(c);
            }
        }
    }
    while(!Optr.empty())
 {
        ans+=Optr.top();
        Optr.pop();
    }
    return ans;
}


//下面就是后缀表达式得出答案的过程，由于比较简单，这个过程由读者自己思考，小熊在这里只给出源码：
double CCalculatorDlg::SuffixToResult(CString szSuffix)
{
 double res;
    stack<double>OpNb;
    for(int i=0;i<szSuffix.GetLength();i++){
        if(szSuffix[i] == lNumFront) //如遇到数字分隔符号
  {
            int nSta = ++i,nCount = 1;
            while(rNumBack!=szSuffix[i]) {i++;nCount++;}
            OpNb.push(atof(szSuffix.Mid(nSta,nCount) ));
        }
        else{ //遇到运算符
            double lt,rt,tmp;
            rt = OpNb.top();OpNb.pop();
            lt = OpNb.top();OpNb.pop();
            switch (szSuffix[i])
            {
            case '+':
                tmp = lt+rt;
                break;
            case '-':
                tmp = lt-rt;
                break;
            case '*':
                tmp = lt*rt;
                break;
            case '/':
                tmp = lt/rt;
                break;
            case '^':
                tmp = pow(lt,rt);
                break;
            }
            OpNb.push(tmp);
        }
    }
    res = OpNb.top();OpNb.pop();
    return res;
}

二、将M进制转化为N进制

方法：先将M进制转化为10进制，然后将10进制转化为N进制。

①、先将M进制转化为10进制

比如：123（6） 到 10进制
nDecRes =  (((1*6)+2)*6+3)

②、将10进制转化为N进制

辗转相除法：

比如：11（10） 转化为 2进制
我们的做法是辗转相除，不断的取余、除2，直到除数为 0

最后，给出源代码：

CString CConvertCal::Convert(CString szInput,INT nSrc,INT nDst)
{
 CString szAns = "";
    INT nTmp,i,j;
    INT nDecRes = 0;
    //src进制转为十进制
    for( i = 0;i < szInput.GetLength();i++){
        if(szInput[i] >= '0' && szInput[i] <= '9'){
            nTmp = szInput[i] - '0';
        }
        else{
            nTmp = szInput[i] - 'A' + 10;
        }
        nDecRes  = nDecRes*nSrc + nTmp;
    }

    //将十进制转为dst进制
    int nDiv = nDecRes,nRem;
    do{
        nRem = nDiv%nDst;
        nDiv = nDiv/nDst;
        if(nRem >= 0&&nRem <= 9)
  {
            szAns+=('0'+nRem);
        }
        else
  {
            szAns+=('A'+nRem-10);
        }
    }while(nDiv != 0);
 //将szAns逆序
    for( i = 0,j = szAns.GetLength()-1;i < j;i++,j--){
  TCHAR ctmp = szAns[i];
  szAns.SetAt(i,szAns[j]);
  szAns.SetAt(j,ctmp);
    }
    return szAns;
}

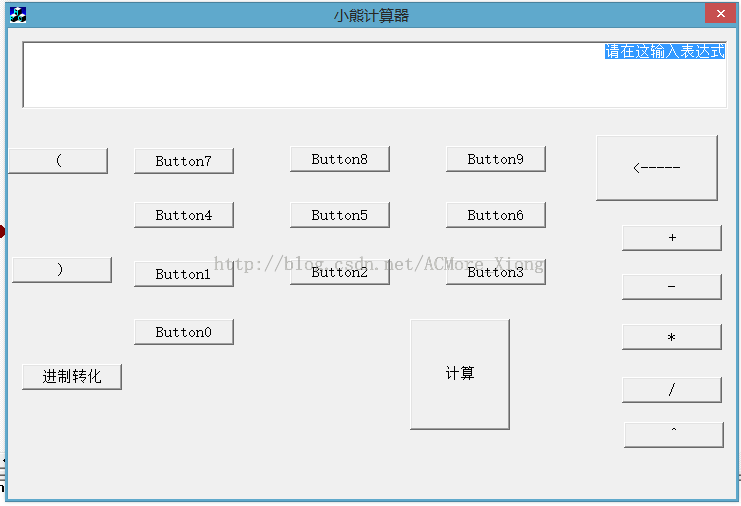
//附上小熊计算器的效果图