栈(2)--栈的应用

一:数制转换

void Conversion ( )  {
// 对于输入的任意一个非负十进制整数，输出等值的八进制数
   InitStack(&S); // 构造空栈
   scanf ("%d",N);
   while (N) {
        Push(&S, N % 8);
        N = N/8;  }
   while (!StackEmpty(S)) {
       Pop(&S,&e);
       printf ( "%d", e );  }
 } // conversion

二.括号匹配

算法思想:

1.凡是有左括号的就入栈;

2.凡是有右括号的，检查栈是否为空

   (1)是：右括号是多余的

   (2)否:出栈顶元素与之比较，若为左括号，则匹配成功

3.当检查完毕时:

  (1)若栈空，则匹配成功;

  (2)栈不空，则有多余的左括号

status matching(string &exp) 
{
// 检验表达式中所含括弧是否正确嵌套，
  int state = 1;
  while ( i <= length(exp) && state)  
  {
     swith of exp[i]  {
       case “(”: { Push(&S,exp[i]); i++; break; }
       case “)”: { if ( ！StackEmpty(S) && GetTop(S) = = ‘(‘  ) 
                             {Pop(&S,&e);  i++;} 
                     else state = 0 ;   break; }
       ．．．．．． 
       } // swith
   } // while
  if ( state && StackEmpty(S) ) return OK
  else return ERROR;            
}

三.行编辑程序

我们假设用户输入文本时，用#表示退格，用@表示退行，

举例:   whli##ilr#e（s#*s)
            outcha@putchar(*s=#++);

实际有效的是：
        while (*s)
        putchar(*s++);
算法思想:

1.当用户输入字符非@,非#,非换行时就入栈;

2.输入#时出栈顶元素;

3.输入@时清空栈;

void LineEdit( ) 
{
    InitStack(s);  
    ch = getchar();
    while (ch != EOF) 
    {
        switch (ch) 
        {
            case '#' : Pop(S, c); break;
            case '@': ClearStack(S); break;// 重置S为空栈        

            case '\n': ClearStack(S); break;// 重置S为空栈

            default : Push(S, ch); break; 
        } 
       ch = getchar(); // 从终端接收下一个字符 } DestroyStack(S); }    

四.迷宫求解

算法思路:

do

｛
     if(当前位置可通)
   ｛

           将当前位置插入栈顶；
           if(该位置是出口位置)

                 算法结束；            
           else{

                     切换当前位置的东邻方块为
                     新的当前位置；

                  }      

      ｝
   else

  {

      if(栈不空且栈顶位置尚有其他方向未被探索)
         {

            设定新的当前位置为: 沿顺时针方向旋转
            找到的栈顶位置的下一相邻块；

          }

       if(栈不空但栈顶位置的四周均不可通)
        ｛

             删去栈顶位置； // 从路径中删去该通道块
            若栈不空，则重新测试新的栈顶位置，
           直至找到一个有可通相邻块的位置
           或出栈至栈空；

         ｝
 ｝
｝while (栈不空)；若栈空，则表明迷宫没有通路。

五.表达式求值

1.表达式的三种标识方法：

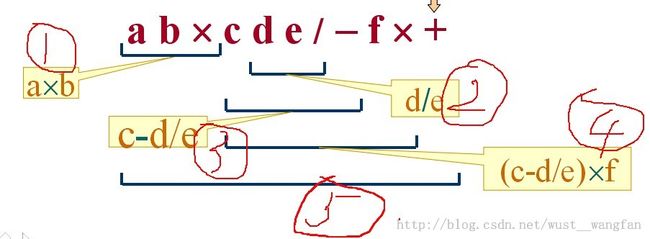
      例如:    Exp = a *b + (c -d / e) *f

      前缀式:           + * a b *- c / d e f
      中缀式:           a* b + c - d / e * f
      后缀式:           a b * c d e / - f * +

      *结论:1）操作数之间的相对次序不变
                 2）运算符的相对次序不同
                 3）中缀式丢失了括弧信息，致使运算的次序不确定;
                 4)前缀式的运算规则为:连续出现的两个操作数和在它们之前且紧靠它们的运算符构成一个最小表达式;
                 5)后缀式的运算规则为:运算符在式中出现的顺序恰为 表达式的运算顺序;每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式

2.由后缀式求值

   (1)方法:先找运算符，再找操作数，运算规则为上面1(5)所示

  

算法思想：

1)初始化操作数栈,若遇到操作数，则操作数入栈;

2)若遇到操作符，则出栈两个操作数，运算之后再把结果入栈,直至后缀表达式依次扫描完

void value(char suffix[ ],int &e)//suffix为后缀式，以"#"结尾
{ char *pch;
   InitStack(S); pch=suffix; //pch指向suffix后缀式的第一个
   while(*pch!=‘#’)
   {
       if(!IN(ch, OP)) 
          push(S,ch);
       else 
         {
          pop(S,a);pop(S,b);push(S,operate(a,ch,b));
         }
        pch++;
   }
    pop(S,e);
}

3.由原表达式求后缀式:

           原表达式:  a + b *c - d / e *f
           后缀式:  a b c * + d e / f * -
          *  结论: 中缀式中每个运算符的运算次序要由它之后的一个运算符来定；

                        后缀式中,优先数高的运算符领先于优先数低的运算符

算法思想：

        1).建立运算符栈并初始化使其栈底为"#",也使表达式最后一个字符为"#";

        2).扫描原表达式，若遇到操作数，则把它加到后缀式;

        3).若遇到运算符，则与栈顶的元素比较，若优先级大于栈顶元素，则入栈;

                                                                               若优先级小于等于栈顶元素，则出栈顶元素并加入到后缀式;

       4).若遇到左括号，则进栈；遇到右括号，则栈中元素依次出栈并加入到后缀式中，直至遇到左括号（左括号也出栈但不加到后缀式中）

     

void transform(char suffix[ ], char exp[ ] ) {
  InitStack(S);  Push(S, '#');//给栈底赋值'#'
  p = exp;  ch = *p;
  while (!StackEmpty(S)) {
      if (!IN(ch, OP)) Pass( Suffix, ch); //如果ch不是操作符，则加到后缀
      else 
          {     
             switch (ch) 
              {
                case '(' :  Push(S, ch); break;
                case ')' :  Pop(S, c);
                            while (c!= '(' )
                              { Pass( Suffix, c);  Pop(S, c) }; break; //如果ch是右括号，则依次出栈并加到后缀，直至遇到左括号
                defult  : //遇到操作符
                while(Gettop(S, c)&&precede(c)>=precede(ch))//若优先级小于等于栈顶元素，则出栈顶元素并加入到后缀式;
                { Pass( Suffix, c);  Pop(S, c); }
                if  ( ch!= '#' )  Push( S, ch); //若优先级大于栈顶元素，则入栈;
                 break;  
              } // switch  
          }
      if ( ch!= '#' ) { p++;  ch = *p; }//扫描表达式的下一个字符
      else { Pop(S, ch);  Pass(Suffix, ch); }//若表达式取得的字符为'#',则符号栈依次出栈
  } // while
} // transform

4.直接从原表达式求值

     举例算exp=a*b+(c-d/e)*f(用以下算法思想模拟整个流程，并尝试把整个代码编写出来)

算法思想:

1).建立两个栈，一个操作符栈operator(OPTR),一个操作数栈operand(OPND),初始化operator栈底为'#'(表达式的最后也加上'#');

2).扫描表达式exp,

    若为操作数，则进栈operand;

    否则为操作符ch:

                         *若ch的优先级大于栈顶元素，则入栈;

                         *若ch的优先级小于等于栈顶元素，则弹出栈顶元素,并从operand栈中弹出两个元素，生成运算指令，把结果入栈到operand,继续处理刚扫描到的ch的操作;

                         @若ch='('左括号,则入栈;

                         @若ch=')'右括号,则看栈顶元素，

                                       若栈顶为'(',则出栈顶元素,继续扫描下个exp字符;

                                       否则出栈一个符号,并从operator中弹出两个操作数生成运算指令,把结果入栈到operand,继续处理当前读入符号;

   若当前读入的ch='#',并且operator栈中也只有'#',则从operand中弹出最后的运算结果，整个流程结束.

OperandType  EvaluateExpression() 
{
  InitStack(OPTR); Push(OPTR,'#'); 
  InitStack(OPND);   c=getchar();
  while(c!=‘#’||GetTop(OPTR)!=‘#’)
  {
    if(!In(c,OP)) {Push((OPND,c); c=getchar();}//操作数
    else
      switch(Precede(GetTop(OPTR),c){
         case ‘<‘: //栈顶元素优先权低
               Push(OPTR,c); c=getchar(); break;
         case ‘=‘: //脱括号并接收下一字符(只有左括号和右括号优先级相等)
               Pop(OPTR,x); c=getchar(); break;
         case ‘>‘: //退栈并将运算结果入栈
               Pop(OPTR, theta); Pop(OPND, b); Pop(OPND, a); 
               Push(OPND, Operate(a, theta, b)); break;
      }//switch
  }//while
  c=Gettop(OPND); //若当前读入的ch='#',并且operator栈中也只有'#',则从operand中弹出最后的运算结果，整个流程结束.
  DestroyStack(OPTR); 
  DestroyStack(OPND); 
  return c;
 }

运算符优先级表如下:θ1在前，θ2在后