機器學習基石(Machine Learning Foundations) 机器学习基石 作业二 课后习题解答
大家好,我是Mac Jiang,首先祝贺大家清明节快乐!作为一名苦逼的程序员,博主只能窝在实验室玩玩游戏,顺便趁着大早上没人发一篇微博。不过还是祝各位出行的兄弟玩的开心!
今天和大家分享coursera-NTU-機器學習基石(Machine Learning Foundations)-作业二的习题解答。笔者在做这些题目时遇到很多困难,当我在网上寻找答案时却找不到,而林老师又不提供答案,所以我就想把自己做题时对题目如何思考的写下来,为大家提供一些思路。当然,我对题目的理解不一定是正确的,如果各位博友发现错误请及时留言联系,谢谢!再次提醒:请不要以此博客作为通过考试的用途,还是更好学习、理解课程的途径!希望我的博客对您的学习有所帮助!
本文出处: http://blog.csdn.net/a1015553840/article/details/51043019
1.第一题
(1)题意:目标函数f的错误率为mu,在样本上加了噪声使得p(x/y)如上面公式(这里1-lambda就是噪声比例,由于输出y是二元的,所以加噪声的意思就是把原来的f(x)变号,成为y),求一个hyphothesis h的有噪声的y的错误率。
(2)分析:这里解决的是二元分类问题,即y={-1,+1}。那么这里加噪声的意思就是1-lamba比例的(x,y)变成(x,-y)了。
当y=f(x)时,由题意我们知道h对f的错误率为mu,而y=f(x)概率为lambda,所以这部分的错误率为lambda*mu。
当y不等于f(x)时,由于我们只是把y的符号翻转了,所以原来正确的变成错误的,原来错误的变成正确的,故此处h对f的错误率为1-mu,这部分错误率为(1-lambda)(1-mu)
(3)答案:第三项
2.第二题
(1)题意:当lambda取何值时,h的表现(此处就是指错误率)会独立于mu?
(2)分析:我们在上面的到了错误率计算公式了,我们的目的是把mu化解掉,很简答,lambda=0.5时候错误率和mu无关,总错误率为0.5
(3)答案:0.5
3.第三题
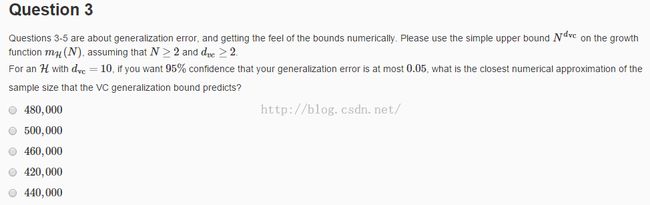
(1)题意:当N大于等于2,d_vc大于等于2时,我们可以用N^d_vc代替mH(N)。当d_vc = 10时,你想要95%的置信率,epsilon小于等于0.05,那么我们需要多要样本(N)?
(2)分析:这道题很简单,带入老师上课讲的公式计算就可以了。

(3)答案:460,000
4.第四题
(1)题意:d_vc=50,置信率为1-delta,delta = 0.05,训练样本数为N。当N = 10000时,分别用下面五个公式计算epsilon的值,哪个最小(最紧)?
(2)分析:没办法,用计算器计算。我算出来的结果Otiginal VC bound=0.63,Radenmacher Penalty Bound = 0.33,Parrondo and Van den Broek=0.224,devroye = 0.215,Variant VC bound=0.86
(3)答案: Decoroye
5.第五题
(1)题意:当N = 5时,分别计算,哪个最小
(2)分析:Original VC bound=13.83,Radenmacher Penalty Bound=7.04,Parrondo and Van den Broek=4.7,devroye=4.9,Variant VC bound=16.2
(3)答案:Parrando and Van den Broek
6.第六题
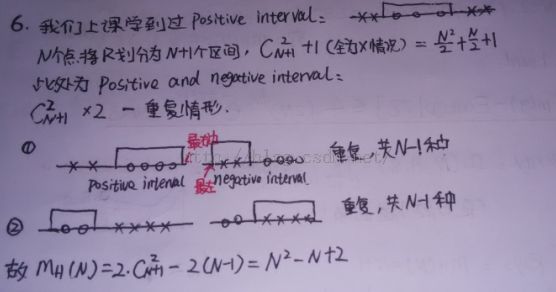
(1)题意:positive and negatibe intervals on R的mH(N)为多少?
(3)答案:N^2 - N +2
7.第七题
(1)题意:Positive and Negative的VC-dimension
(2)分析:我们已经求得mH(N) = N^2-N+2。当N=1,mH(1)=2=2^(1);当N=2,mH(2)=4=2^2,当N=3,mH(3)=8=2^3;当N=4,mH(4)=16!=2^4
(3)答案:3
8.第八题
(1)题意:利用x1^2+x2^2作为分类线,形成两个同心圆,在同心圆里面的归为+1类,在同心圆外面的归为-1类。假设有N个样本,求mH(N)
(2)分析:仔细想一想,这个问题和一位的positive Interval是一个问题,只是维度从一维变成二维
(3)答案:最后一项
9.第九题
(1)题意:多项式判别的Hyphothesis如上面图所示,求H得d_vc
(2)分析:从H可以看出,这道题就是perceptrons,即PLA算法的实现。而我们在课堂上已经证明过,他的d_vc = D+1
(3)答案:D+1
10.第十题
博主也不会!求大神解答。
11.第十一题
(1)题意:H的定义如上图,求H得d_vc、
(2)分析:其实可以作图发现H是方波,考虑N=1,N=2,N=3的情况都是可以得到2^N的分类方法,推广到N维就可以了
(3)答案:无穷
12.第十二题
(1)题意:下列哪些式子是成长函数mH(N)的上限函数,当N大于等于d_vc大于等于2
(2)分析:在上课的时候老师说过,当d_vc 大于等于2,N大于等于2时,mH(N)的上限函数为N^d_vc,所以第二项错误了。对于第三项,在N小于d_vc之前都是正确的,但是当N大于d_vc,那么他的mH(N)一定是大于他的,错误。第一项莫名其妙,错误。
第四项,展开i=1部分,2*mH(N-1),其实这么一部分就比mH(N)大了。试想,d_vc为无穷,分类数为2^N,N每增加1,分类个数就增加一倍。 而此处d_vc!=无穷,那么他每次增长倍数小于2,故小于2*mH(N-1)。----其实,可以从B(N,K)哪个表格中找找思路!
(3)答案:第四项
13.第十三题
(1)题意:下面哪些mH(N)是不可能的
(2)分析:mH(N)是单增的,而第四项并不是。其实这道理博主也没能理解透彻,不过好像是因为第四项不是严格单增的
(3)答案:第四项
14.第十四题
(1)题意:下面这些选项中有的是正确的,有的是错误的。在正确的选项中找到范围最小的。
(2)分析:这道题求的是并集合的d_vc。
首先,我们看左边边界。若有一个Hk是空集,那么d_vc=0,所以最小值是0
之后,我们看右边边界。由于是交集,我们最多保留最小的d_vc
(3)答案:第四项
15.第十五题
(1)题意:在考虑了交集情况,讨论并情况
(2)分析:a.左边:H1...Hk能做的并集也能做,故为max
b.右边的问题是有没有K-1。试想,有一个H1,把平面所有点分为+1,H2把平面所有点分为-1。H1并H2的话为VC dimension为1,而各自d_vc加起来为0
(3)答案:第四项
第16-18题: http://blog.csdn.net/a1015553840/article/details/51023193
第19-20题: http://blog.csdn.net/a1015553840/article/details/51029765
本文出处: http://blog.csdn.net/a1015553840/article/details/51043019