Studying note of GCC-3.4.6 source (176)

5.13.5.3.2.2.1.          Sort by invocation order

Out of aiding below processing, at line 1253, put all cgraph_node in the order of invocation, and transform the direct graph into queue (it satisfies the definition of topological order).

 

548  static int

549  cgraph_postorder (struct cgraph_node **order)                                           in cgraphunit.c

550  {

551    struct cgraph_node *node, *node2;

552    int stack_size = 0;

553    int order_pos = 0;

554    struct cgraph_edge *edge, last;

555 

556    struct cgraph_node **stack =

557      xcalloc (cgraph_n_nodes , sizeof (struct cgraph_node *));

558 

559    /* We have to deal with cycles nicely, so use a depth first traversal

560      output algorithm. Ignore the fact that some functions won't need

561      to be output and put them into order as well, so we get dependencies

562      right through intline functions.  */

563    for (node = cgraph_nodes ; node; node = node->next)

564      node->aux = NULL;

565    for (node = cgraph_nodes ; node; node = node->next)

566      if (!node->aux)

567      {

568        node2 = node;

569        if (!node->callers)

570           node->aux = &last;

571        else

572           node->aux = node->callers;

573        while (node2)

574         {

575           while (node2->aux != &last)

576           {

577            edge = node2->aux;

578            if (edge->next_caller)

579               node2->aux = edge->next_caller;

580            else

581               node2->aux = &last;

582            if (!edge->caller->aux)

583             {

584               if (!edge->caller->callers)

585                 edge->caller->aux = &last;

586               else

587                 edge->caller->aux = edge->caller->callers;

588               stack[stack_size++] = node2;

589               node2 = edge->caller;

590               break ;

591             }

592           }

593           if (node2->aux == &last)

594           {

595            order[order_pos++] = node2;

596            if (stack_size)

597               node2 = stack[--stack_size];

598            else

599               node2 = NULL;

600           }

601         }

602      }

603    free (stack);

604    return order_pos;

605  }

 

Alogrithm used here is that first proposed by Kahn in 1962, its detail is given below:

L ← Empty list that will contain the sorted elements

S ← Set of all nodes with no incoming edges

while

 S is non-empty do

    
remove a node n from S

    
insert n into L

    
for each
 node m with an edge e
 from n to m do

        
remove edge e from the graph

        
if
 m has no other incoming edges then

            
insert m into S

if

 graph has edges then

    
output error message (graph has at least one cycle)

else

 

    
output message (proposed topologically sorted order: L)

However in here implementation, cycle isn’t a problem (it caused by direct or indirect recursion), as C++ program always begins with function main, when cycle appears, it begins with the node most far away from main. No doubt, recursed function can’t be inlined, or it will cause infinite expansion. But we don’t treat it here.

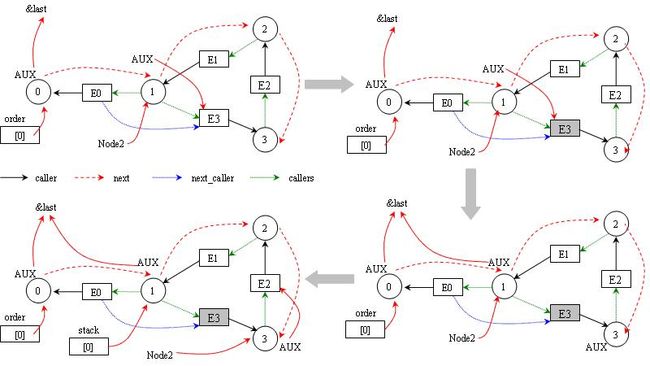
Take below invocation relation as example, we have known cgraph_node is built in its first time invocation, so their order in cgraph_nodes reflect the order of the time of invocation. In below figures, the order of the time of invocation is: 0 -> 1 -> 2 -> 3 -> 1.

Figure 119 : handling node 0

As function 0 hasn’t caller, clearly, it’s the first node after sorting.

 

Figure 120 : handling of node 1

Function 1 appears in a cycle, thus its node’s AUX follows to next caller’s cgraph_edge.

Figure 121 : handling node 1 in second time

Treating function 1 again, cache it into stack, and enter its next caller.

Figure 122 : handling of node 3

Step into call chain of function 1, function 3 is still not the final caller, cache it into stack too.

Figure 123 : handling of node 2

Function 2 at the head of the call chain of function 1, but it is also called by function 1, howeverfunction 1 hasn’t been handled, so accept it as sorted node.

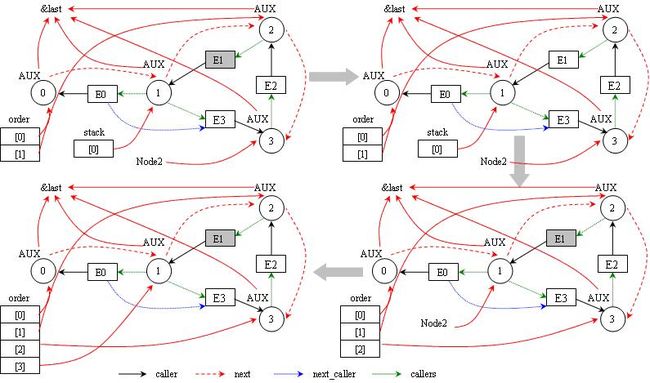
Figure 124 : handling of nodes in stack

Nodes in the stack then are fetched in LIFO order and put into the sorted queue. The sorted queue is:  0 -> 2 -> 3 -> 1 。