数据结构(14)--线索二叉树的实现

参考书籍：数据结构（C语言版）严蔚敏吴伟民编著清华大学出版社

1.什么是线索二叉树

    空的左孩子指针指向该结点的前驱；空的右孩子指针指向该结点的后继。这种附加的指针值称为线索，带线索的二叉树称为线索二叉树。 

    在不同的遍历次序下，二叉树中的每个结点一般有不同的前驱和后继。因此，线索二叉树又分为前序线索二叉树、中序线索二叉树和后序线索二叉树3种。 

    根据二叉树的特性，n个结点的二叉树，采用链式存储结构时，有n+1个空链域，可以利用这些空链域存放指向结点的直接前驱和直接后继结点的指针。为此做如下规定：当结点的左指针为空（即无左子树）时，令该指针指向按某种方式遍历二叉树时得到的该结点的前驱结点；当结点的右指针为空（即无右子树）时，令该指针指向按某种方式遍历二叉树时得到的该结点的后继结点；为了避免混淆，还需要增加两个标志位来区分指针指向的是其孩子还是前驱及后继。

2.建立线索二叉树

    线索化的过程就是遍历二叉树的过程。在遍历的过程中，检查当前结点的左、右指针域是否为空，若为空，将它们改为指向前驱结点或后继结点的线索。

    当线索花二叉树以后，遍历二叉树的时间复杂度虽然仍然是O(n)，但常数因子要比上一篇博文中的算法小，且不需要设栈。因此如果程序中所用的二叉树需要经常遍历或查找结点在遍历所得的线性序列的前驱和后继，则应采用线索链表作为二叉树的存储结构。

    线索二叉树上的查找：例如中序线索化二叉树以后，结点的后继要么右标志为1，后继直接是右线索所指的结点，要么是遍历其右子树时访问的第一个结点，即右子树中最左下的结点；而结点的前驱要么左标志为1，前驱就是左线索所指的结点，要么是遍历其左子树时访问的最后一个结点，即左子树中最右下的结点。

    为方便起见。仿照线性表的存储结构，在二叉树的线索链表上也添加一个头结点，并令其lchild域的指针指向二叉树的根结点，其rchild域的指针指向中序遍历时访问的最后一个结点；反之，令二叉树的中序序列中的第一个结点的lchild域指针和最后一个节点的rchild域的指针均指向头结点。这好比为二叉树建立了一个双向线索链表，既可以从第一个结点起顺后继进行遍历，也可以从最后一个结点起，顺前驱进行遍历。

3.代码实现

下面以中序线索化二叉树为例进行实现。

3.1线索二叉树的定义

#include<stdio.h>
#include<stdlib.h>

//#define Link 0//指针标志
//#define Thread 1//线索标志
typedef char TElemType; 
//中序线索二叉树
typedef enum PointerTag {Link, Thread};//结点的child域类型，link表示是指针，指向孩子结点，thread表示是线索，指示前驱或后继结点
//补充：枚举型是一个集合，集合中的元素(枚举成员)是一些命名的整型常量，元素之间用逗号隔开
//第一个枚举成员的默认值为整型的0，后续枚举成员的值在前一个成员上加1。
//可以人为设定枚举成员的值，从而自定义某个范围内的整数。

typedef struct ThrBiNode{
	TElemType data;
	ThrBiNode *lchild, *rchild;//左右孩子指针
	PointerTag lTag, rTag;//左右标志
}ThrBiNode, *ThrBiTree;

3.2中序线索化二叉树

    线索划的过程即为在遍历的过程中修改空指针的过程，为记下遍历过程中访问结点的先后顺序，附设指针pre总指向当前访问结点p的前驱结点。

//中序遍历二叉树T，并将其 中序线索化，Thrt指向头结点
void inOrderThreading(ThrBiTree T, ThrBiTree &Thrt){
	//初始化线索链表，为其建立一个头结点
	Thrt = (ThrBiTree)malloc(sizeof(ThrBiNode));
	Thrt->lTag = Link;
	Thrt->rTag = Thread;
	//Thrt->rchild = Thrt;//右指针回指，因为若T为空树的话，只会指向下面的if语句，那么Thrt->rchild
	if(!T){//如果二叉树为空树，则Thrt->lchild指针回指
		Thrt->lchild = Thrt;
		Thrt->rchild = Thrt;//右指针回指
	}else{
		Thrt->lchild = T;
		ThrBiNode *pre = Thrt;//pre指针总指向当前结点的前驱结点
		inThreading(T, pre);
		//继续为最后一个结点加入线索
		//此时pre应指向最后一个结点
		pre->rTag = Thread;
		pre->rchild = Thrt;//最后一个结点的rchild域指针回指
		Thrt->rchild = pre;//头结点的rchild域指针指向最后一个结点
	}
}

//中序遍历进行中序线索化(左、根、右)
void inThreading(ThrBiTree T, ThrBiTree &pre){
	if(T){
		inThreading(T->lchild, pre);//左子树线索化

		if(!T->lchild){//当前结点的左孩子为空
			T->lTag = Thread;
			T->lchild = pre;
		}else{
			T->lTag = Link;
		}

		if(!pre->rchild){//前驱结点的右孩子为空
			pre->rTag = Thread;
			pre->rchild = T;
		}else{
			pre->rTag = Link;
		}
		pre = T;		
		inThreading(T->rchild, pre);//右子树线索化
	}
}

3.3中序遍历线索二叉树

//T指向头结点，头结点的lchild链域指针指向二叉树的根结点
//中序遍历打印二叉线索树T（非递归算法）
void inOrderTraversePrint(ThrBiTree T){
	ThrBiNode *p = T->lchild;//p指向根结点
	
	while(p != T){//空树或遍历结束时，p == T
		while(p->lTag == Link){
			p = p->lchild;
		}
		//此时p指向中序遍历序列的第一个结点（最左下的结点）

		printf("%c ", p->data);//打印（访问）其左子树为空的结点

		while(p->rTag == Thread && p->rchild != T){
			p = p->rchild;
			printf("%c ", p->data);//访问后继结点
		}
		//当p所指结点的rchild指向的是孩子结点而不是线索时，p的后继应该是其右子树的最左下的结点，即遍历其右子树时访问的第一个节点
		p = p->rchild;
	}
	printf("\n");
}

3.4创建二叉树

//利用先序序列建立一颗二叉树,'.'代表空树
//测试用例1：abc..de.g..f...#
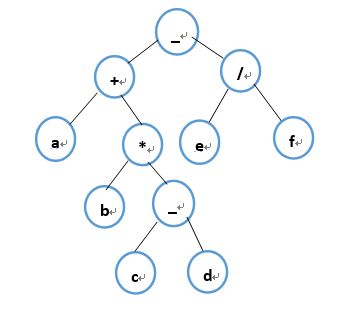
//测试用例2:-+a..*b..-c..d../e..f..#
void createBiTreeByPreOrder(ThrBiTree &T){
	//按先序次序输入二叉树中节点的值（一个字符），点号字符表示空树，构造二叉链表表示的二叉树
	//注意：若输入的字符数（不含#号）为n个，则相应的空树即点号就应该有n+1个
	char ch;
	scanf("%c", &ch);
	if(ch != '#'){
		if(ch == '.'){
			T = NULL;
		}else{
			T = (ThrBiNode *)malloc(sizeof(ThrBiNode));
			T->data = ch;
			createBiTreeByPreOrder(T->lchild);
			createBiTreeByPreOrder(T->rchild);
		}
	}
}

3.5演示

测试用例

二叉树：

  测试输入：-+a..*b..-c..d../e..f..#

对应的中序线索二叉树：

void main(){
	ThrBiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);//建立二叉树
	
	ThrBiTree Thrt;
	inOrderThreading(T, Thrt);//将二叉树T中序线索化

	inOrderTraversePrint(Thrt);//中序遍历二叉线索树（通过线索链表，就像访问线性表一样）
	//当然之前的不按线索，直接根据二叉树的结构进行遍历依然可以（层次、先序、后序、中序）
}