MATLAB谢菲尔德遗传算法工具箱使用

种群表示和初始化

函数 bs2rv:  二进制串到实值的转换

             Phen=bs2rv(Chrom,FieldD) 

             FieldD=[len, lb, ub, code, scale, lbin, ubin]

len是字串的长度，lb和ub是每个变量的下界和上界，lbin和ubin指明表示范围中是否包含边界，0不包括，1包括。

             code(i)=1为标准的二进制编码，code(i)=0为格雷编码

             scale(i)=0为算术刻度，scale(i)=1为对数刻度

函数 crtbp:  创建初始种群

            [Chrom,Lind,BaseV]=crtbp(Nind,Lind)    

            [Chrom,Lind,BaseV]=crtbp(Nind,BaseV)

            [Chrom,Lind,BaseV]=crtbp(Nind,Lind,BaseV)

             Nind指定种群中个体的数量，Lind指定个体的长度，Basev与base是一样的，返回的是个体的各个位的进制数

函数 crtrp:  创建实值原始种群

            Chrom=crtrp(Nind,FieldDR)

适应度计算

函数 ranking:  基于排序的适应度分配（此函数是从最小化方向对个体进行排序的）

              FitV=ranking(ObjV)

              FitV=ranking(ObjV, RFun)

              FitV=ranking(ObjV, RFun, SUBPOP)

              Rfun(1)线性排序标量在[1 2]间，代表的是选择压差，比如压差为2，那就限制了Objv的结果fitv在0-2之间，如果是1.5，就在0.5-1.5之间，结果的最大值与最小值加起来就是2，非线性排序在[1 length(ObjV)-2]

              Rfun(2)指定排序方法，0为线性排序，1为非线性排序

              SUBPOP指明ObjV中子种群的数量，默认为1

其实我对这个函数没了解得太深刻，不过我觉得这是一种变比技术。将原先的适应度值压缩到一定的范围，而且目标值越大，分配的适应度值越小。例如 A=[1;2;3;4;2;3];
   ranking(A)= 2.0000    1.4000    0.6000         0    1.4000    0.6000，所以如果是求最大值，就得-A，求最小值就直接A就可以了，因为目标值越大分配的适应度越小，目标值越小，分配的适应度越大。ranking的结果FitV只在select选择的时候有用到，这只是一种个体选择概率的常用分配方法之一

关于个体选择概率的常用分配方法参考：http://wenku.baidu.com/link?url=U9fHrBvJg2YMac-7ckdcLGs9EtXgxzmux6ahLrYlMZWiJBfbzekkdtaKERaD0ZO6hsY56RzTTiIQds4Vn0fysPKSaYSPcpQ1qFcLxp22LWy

选择

高级函数 select:  从种群中选择个体

                SelCh=select(SEL_F, Chrom, FitnV)

                SelCh=select(SEL_F, Chrom, FitnV, GGAP)

                SelCh=select(SEL_F, Chrom, FitnV, GGAP, SUBPOP)

                SEL_F是一字符串，为一低级选择函数名，如rws或sus

                GGAP指出了代沟，默认为1；也可大于1，允许子代数多于父代的数量

SUBPOP是指子代种群的个数

rws: 轮盘赌选择

     NewChrIx=rws(FitnV, Nsel) 使用轮盘赌选择从一个种群中选择Nsel个个体

     NewChrIx 是为育种选择的个体的索引值

sus:  随机遍历抽样

     NewChrIx=sus(FitnV, Nsel)

关于选择方法的介绍及比较参考：http://wenku.baidu.com/link?url=fyc9LUjso9IJmYhEKd7fnLl_25CsTdGZEm1CyCtHaDj2DtYe5K9IQCcY7DhcHD-dTlsgdgjobsImdOQUr4MmKm9CytLBsUU1oLCBLyn4uVO

交叉

高级函数 recombin:  重组个体

                    NewChrom=recombin(REC_F, Chrom)

                    NewChrom=recombin(REC_F, Chrom, RecOpt)

                    NewChrom=recombin(REC_F, Chrom, RecOpt, SUBPOP)

chrom是待交叉的种群，recopt是交叉概率，subpop是一个决定子种群个数的可选参数，默认是1，chrom中所有子种群的大小必须一致。

                    REC_F是包含低级重组函数名的字符串，交叉方式，例如recdis,recint,reclin,xovdp, xovdprs, xovmp, xovsh, xovshrs, xovsp, xovsprs

recdis:    离散重组

          NewChrom=recdis(OldChorm)

recint:    中间重组

          NewChrom=recint(OldChorm)

reclin:    线性重组

          NewChrom=reclin(OldChorm)

xovdp:    两点交叉

          NewChrom=xovdp(OldChrom, XOVR)

          XOVR为交叉概率， 默认为0.7

Xovdprs:  减少代理的两点交叉

          NewChrom=xovdprs(OldChrom, XOVR)

Xovmp:   多点交叉

          NewChrom=xovmp(OldChrom, XOVR, Npt, Rs)

          Npt指明交叉点数， 0 洗牌交叉；1 单点交叉；2 两点交叉；  默认为0

          Rs指明使用减少代理， 0 不减少代理；1 减少代理；  默认为0

Xovsh:    洗牌交叉

          NewChrom=xovsh(OldChrom, XOVR)

Xovshrs:  减少代理的洗牌交叉

          NewChrom=xovshrs(OldChrom, XOVR)

Xovsp:    单点交叉

          NewChrom=xovsp(OldChrom, XOVR)

Xovsprs:  减少代理的单点交叉

          NewChrom=xovsprs(OldChrom, XOVR)

变异

高级函数 mutate:  个体的变异

                  NewChorm=mutate(MUT_F, OldChorm, FieldDR)

NewChorm=mutate(MUT_F, OldChorm, FieldDR, MutOpt)

NewChorm=mutate(MUT_F, OldChorm, FieldDR, MutOpt, SUBPOP)

MUT_F为包含低级变异函数的字符串，例如mut, mutbga, recmut

mut:  离散变异算子

      NewChrom=mut(OldChorm, Pm)

NewChrom=mut(OldChorm, Pm, BaseV)

      Pm为变异概率，默认为Pm=0.7/Lind，basev是染色体的各个位的进制数，目前只用过这个

mutbga:  实值种群的变异（遗传算法育种器的变异算子）

NewChrom=mutbga(OldChorm, FieldDR)

          NewChrom=mubga(OldChorm, FieidDR, MutOpt)

          MutOpt(1)是在[ 0 1]间的重组概率的标量，默认为1

          MutOpt(2)是在[0 1]间的压缩重组范围的标量，默认为1（不压缩）

recmut:   具有突变特征的线性重组

          NewChrom=recmut(OldChorm, FieldDR)

          NewChrom=recmut(OldChorm, FieidDR, MutOpt)

         

重插入

函数 reins:  重插入子群到种群

            Chorm=reins(Chorm, SelCh)

            Chorm=reins(Chorm, SelCh, SUBPOP)

            Chorm=reins(Chorm, SelCh, SUBPOP, InsOpt, ObjVch)

            [Chorm, ObjVch]=reins(Chorm, SelCh, SUBPOP, InsOpt, ObjVch, ObjVSel)

Chorm, 父代种群，SelCh子代种群

            InsOpt(1)指明用子代代替父代的选择方法，0为均匀选择，1为基于适应度的选择，默认为0

            InsOpt(2)指明在[0 1]间每个子种群中重插入的子代个体在整个子种群的中个体的比率，默认为1

            ObjVch包含Chorm中个体的目标值，对基于适应度的重插入是必需的

            ObjVSel包含Selch中个体的目标值，如子代数量大于重插入种群的子代数量是必需的

其他函数

矩阵复试函数 rep:  MatOut=rep(MatIn, REPN)   REPN为复制次数

使用案例：

clc
clear all
close all
%% 画出函数图
figure(1);
hold on;
lb=1;ub=2; %函数自变量范围【1,2】
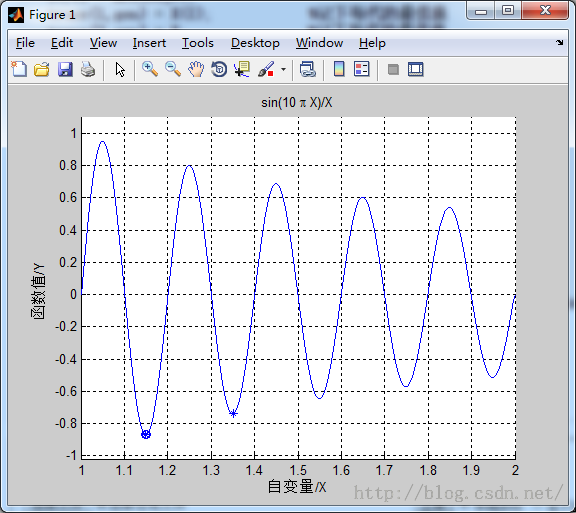
ezplot('sin(10*pi*X)/X',[lb,ub]);   %画出函数曲线
xlabel('自变量/X')
ylabel('函数值/Y')
%% 定义遗传算法参数
NIND=40;        %个体数目
MAXGEN=20;      %最大遗传代数
PRECI=20;       %变量的二进制位数
GGAP=0.95;      %代沟
px=0.7;         %交叉概率
pm=0.01;        %变异概率
trace=zeros(2,MAXGEN);                        %寻优结果的初始值
FieldD=[PRECI;lb;ub;1;0;1;1];                      %区域描述器
Chrom=crtbp(NIND,PRECI);                      %初始种群
%% 优化
gen=0;                                  %代计数器
X=bs2rv(Chrom,FieldD);                 %计算初始种群的十进制转换
ObjV=sin(10*pi*X)./X;        %计算目标函数值
while gen<MAXGEN
   FitnV=ranking(ObjV);                               %分配适应度值
   SelCh=select('sus',Chrom,FitnV,GGAP);              %选择，随机遍历选择
   SelCh=recombin('xovsp',SelCh,px);                  %重组，单点交叉
   SelCh=mut(SelCh,pm);                               %变异
   X=bs2rv(SelCh,FieldD);               %子代个体的十进制转换
   ObjVSel=sin(10*pi*X)./X;             %计算子代的目标函数值
   [Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代，得到新种群
   %chrom是父代种群，selch是子代，1，子种群数目都是1,1，基于适应度的选择，用子代代替父代适应度最小的个体
   X=bs2rv(Chrom,FieldD);
   gen=gen+1;                                             %代计数器增加
   %获取每代的最优解及其序号，Y为最优解,I为个体的序号
   [Y,I]=min(ObjV);
   trace(1,gen)=X(I);                            %记下每代的最优值
   trace(2,gen)=Y;                               %记下每代的最优值
end
figure(2);
plot(trace(1,:),trace(2,:),'bo');                            %画出每代的最优点
grid on;
plot(X,ObjV,'b*');   %画出最后一代的种群
title('每代的最优点')
%此时x中存的是最后一代种群的所有个体的十进制值
hold off
%% 画进化图
figure(3);
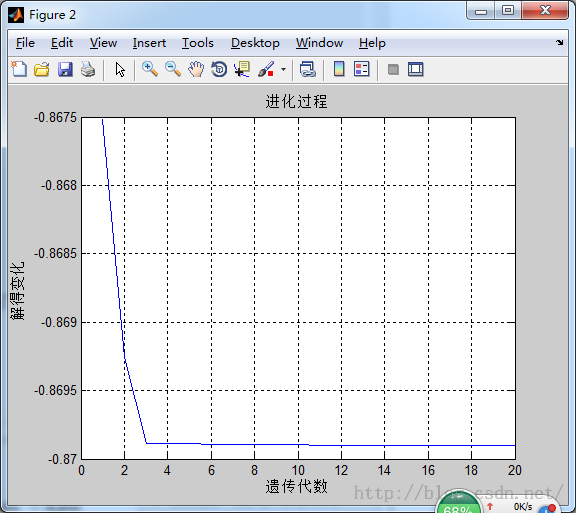
plot(1:MAXGEN,trace(2,:));
grid on
xlabel('遗传代数')
ylabel('解的变化')
title('进化过程')
bestY=trace(2,end);
bestX=trace(1,end);
fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\n'])

运行结果：

案例2：

clc
clear all
close all
%% 画出函数图
figure(1);
lbx=-2;ubx=2; %函数自变量x范围【-2,2】
lby=-2;uby=2; %函数自变量y范围【-2,2】
ezmesh('y*sin(2*pi*x)+x*cos(2*pi*y)',[lbx,ubx,lby,uby],50);   %画出函数曲线
hold on;
%% 定义遗传算法参数
NIND=40;        %个体数目
MAXGEN=50;      %最大遗传代数
PRECI=20;       %变量的二进制位数
GGAP=0.95;      %代沟
px=0.7;         %交叉概率
pm=0.01;        %变异概率
trace=zeros(3,MAXGEN);                        %寻优结果的初始值
FieldD=[PRECI PRECI;lbx lby;ubx uby;1 1;0 0;1 1;1 1];                      %区域描述器
Chrom=crtbp(NIND,PRECI*2);                      %初始种群
%% 优化
gen=0;                                  %代计数器
XY=bs2rv(Chrom,FieldD);                 %计算初始种群的十进制转换
X=XY(:,1);Y=XY(:,2);
ObjV=Y.*sin(2*pi*X)+X.*cos(2*pi*Y);        %计算目标函数值
while gen<MAXGEN
   FitnV=ranking(-ObjV);                              %分配适应度值，因为这里是求最大值，所以改成了负的
   SelCh=select('sus',Chrom,FitnV,GGAP);              %选择
   SelCh=recombin('xovsp',SelCh,px);                  %重组，单点交叉
   SelCh=mut(SelCh,pm);                               %变异
   XY=bs2rv(SelCh,FieldD);               %子代个体的十进制转换
   X=XY(:,1);Y=XY(:,2);
   ObjVSel=Y.*sin(2*pi*X)+X.*cos(2*pi*Y);             %计算子代的目标函数值
   [Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代，得到新种群
  % 1，子种群的个数是1,1，基于适应度的选择，子代代替父代中适应度最小的个体
   XY=bs2rv(Chrom,FieldD);
   gen=gen+1;                                             %代计数器增加
   %获取每代的最优解及其序号，Y为最优解,I为个体的序号
   [Y,I]=max(ObjV);
   trace(1:2,gen)=XY(I,:);                       %记下每代的最优值
   trace(3,gen)=Y;                               %记下每代的最优值
end
plot3(trace(1,:),trace(2,:),trace(3,:),'bo');                            %画出每代的最优点
grid on;
plot3(XY(:,1),XY(:,2),ObjV,'bo');  %画出最后一代的种群
hold off
%% 画进化图
figure(2);
plot(1:MAXGEN,trace(3,:));
grid on
xlabel('遗传代数')
ylabel('解的变化')
title('进化过程')
bestZ=trace(3,end);
bestX=trace(1,end);
bestY=trace(2,end);
fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\nZ=',num2str(bestZ),'\n'])

结果与上一个相似，就不贴图了，这里只想补充一点：谢菲尔的工具箱中的ranking函数是依据目标函数的值进行适应度分配的，目标函数的值越大，适应度分配越小，目标函数的值越小，适应度分配的结果就越大，我们选择的时候是依据适应度值越大选择的概率就越大的方式去选择，所以当求最小值的时候，直接将目标函数值代入ranking函数中即可，而在求最大值的时候要代入负的目标值，这样最大值就变成了最小值可以得到最大的适应度分配值。另外，ranking函数的结果只在select中会用到，插入的时候用的是目标值。