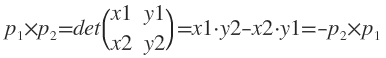HDU 1558 Segment set

A - Segment set

Time Limit:1000MS    Memory Limit:32768KB    64bit IO Format:%I64d & %I64u

Submit Status Practice HDU 1558

Description

A segment and all segments which are connected with it compose a segment set. The size of a segment set is the number of segments in it. The problem is to find the size of some segment set.

 

Input

In the first line there is an integer t - the number of test case. For each test case in first line there is an integer n (n<=1000) - the number of commands.

There are two different commands described in different format shown below:

P x1 y1 x2 y2 - paint a segment whose coordinates of the two endpoints are (x1,y1),(x2,y2).
Q k - query the size of the segment set which contains the k-th segment.

k is between 1 and the number of segments in the moment. There is no segment in the plane at first, so the first command is always a P-command.

 

Output

For each Q-command, output the answer. There is a blank line between test cases.

 

Sample Input

     
     
     
     

      
      
      
      1
10
P 1.00 1.00 4.00 2.00
P 1.00 -2.00 8.00 4.00
Q 1
P 2.00 3.00 3.00 1.00
Q 1
Q 3
P 1.00 4.00 8.00 2.00
Q 2
P 3.00 3.00 6.00 -2.00
Q 5 
     
     
     
     

 

Sample Output

     
     
     
     

      
      
      
      1
2
2
2
5 
     
     
     
     

 

并查集的题，加上判断线段相交，可以用数学上向量叉积的方法。

参考大牛的经验后，总结如下

把p0定为原点，p1的坐标是(x1,y1)，p2的坐标是(x2,y2)。向量的叉积(cross product)实际上就是矩阵的行列式：

当叉积为正时，说明在的顺时针方向上；叉积为0说明两向量共线（同向或反向）。

当同时满足：

（1）和在的两侧（即一个顺时针方向上，一个在逆时针方向上）

（2）和在的两侧

时可肯定和相交。

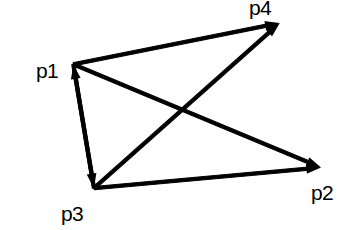
　　　　　　　　　　　　图1

图1是线段相交的一般情形。

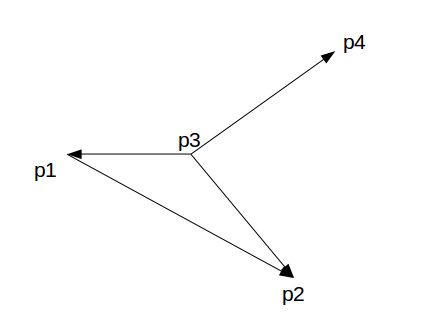
图2只满足第（1）条，不满足第（2）条所以不能证明和相交。

　　　　　　　　　　　　图2

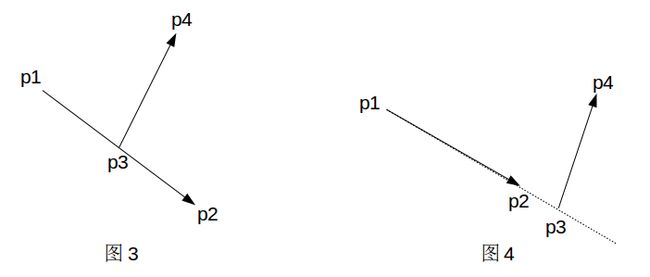
图3和图4是一种特殊情况，它不满足第（2）条，因为和重合,即和的叉积为0。

可见当叉积为0时要分情况讨论，当p3在线段p₁p₂上时两线段相交；当p3在线段p₁p₂的延长线上时两线段不相交。

这题其他的就是简单的并查集了。

可以写结构体来记录查询，或者定义点。

#include <stdio.h>
#include <algorithm>
using namespace std;
typedef struct{
    double x,y;
}Point;
typedef struct{
    Point s,e;
}Pquery;
Pquery a[1005];
int fa[1005];
int ans[1005];
int Find(int x) {
    return fa[x] == x ? x : fa[x] = Find(fa[x]) ;
}

bool Merge(int u ,int v) {
    int fu = Find(u) , fv = Find(v) ;
    if(fu != fv)
    {
        fa[fv] = fu ;
        ans[fu]+=ans[fv];
    }
    return fu != fv ;
}
double mult(Point a, Point b, Point c)
{
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}
bool IsCross(Point aa, Point bb, Point cc, Point dd)
{
    if ( max(aa.x, bb.x)<min(cc.x, dd.x) )
        return false;
    if ( max(aa.y, bb.y)<min(cc.y, dd.y) )
        return false;
    if ( max(cc.x, dd.x)<min(aa.x, bb.x) )
        return false;
    if ( max(cc.y, dd.y)<min(aa.y, bb.y) )
        return false;
    if ( mult(cc, bb, aa)*mult(bb, dd, aa)<0 )
        return false;
    if ( mult(aa, dd, cc)*mult(dd, bb, cc)<0 )
        return false;
    return true;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        for(int i=1; i<=n; i++)
        {
            fa[i] = i;
            ans[i]=1;
        }
        int i=0;
        while(n--)
        {
            char type[5];
            scanf("%s",type);
            if(type[0]=='P')
            {
                i++;
                scanf("%lf%lf%lf%lf",&a[i].s.x,&a[i].s.y,&a[i].e.x,&a[i].e.y);
                for(int j=1;j<i;j++)
                {
                    if(Find(i)!=Find(j)&&IsCross(a[i].s,a[i].e,a[j].s,a[j].e))
                        Merge(i,j);
                }
            }
            else
            {
                int key;
                scanf("%d",&key);
                printf("%d\n",ans[Find(key)]);
            }
        }
        if(t!=0)
            printf("\n");
    }
    return 0;
}