算法导论之哈夫曼编码
今天和大家一起讨论Haffman编码,哈夫曼编码是基于哈夫曼树,也可以被称为最有二叉树,哈夫曼编码可以有效的压缩数据,通常可以节省20%~90%,具体的压缩率依赖于数据的特性。首先给大家介绍一下什么是最优二叉树;在介绍什么是最有二叉树之前,先说明两个概念 ,
i>叶子节点的路径长度:从根到叶子节点的边的个数;
ii>叶子节点的带权路径长度(WPL):叶子节点的权值 * 路径长度;
(1) 最优二叉树(Haffman Tree):一颗二叉树的所有叶子节点的带权路径长度之和最小。
例:有节点 A(9)、B(2)、C(7)、D(4)
第一种构建二叉树的方式:
X
/ \
X X
/ \ / \
A B C D
其WPL值为:(9 + 2+ 7 + 4)* 2 = 44
第二种构建二叉树的方式:
X
/ \
A X
/ \
C X
/ \
B D
将权值大放在靠近根结点的位置;其WPL值为:9 + 7 * 2 + (2 + 4)*3 = 41
(2)构造哈夫曼树 ------->贪心算法
i> 初始 :森林:F = {A(9)、B(2)、C(7)、D(4)}
ii>处理:从森林中选取权值最小和次小的2颗树构建成一颗新二叉树,并放回森林,并删除原来的2颗二叉树
iii>重复ii>,直至森林中只剩一颗二叉树。
例:F = {A、B、C、D}
i> 6
/ \
B D ---> 放回森林,并删除B、D两颗二叉树
(2) (4)
ii> 13
/ \
6 C(7) --->放回森林,并删除6、C两颗二叉树
/ \
B D
(2) (4)
iii> 22
/ \
A 13
(9) / \
6 C(7)
/ \
B D
(2) (4)
在构造二叉树时会遇到以下的几个问题:
A>如何查找权值最小和次小的两颗子树:-------贪心准则
B>如何构建一颗新的子树:
i>创建双亲 ----权值为左右子树之和
ii>左子女 --->最小 右子女 --->次小
C>如何知道森林中只剩下一颗子树 -------->结束条件
i>Haffman树无单分支节点
ii>经过n - 1次就可构建完成
实现Haffman Tree
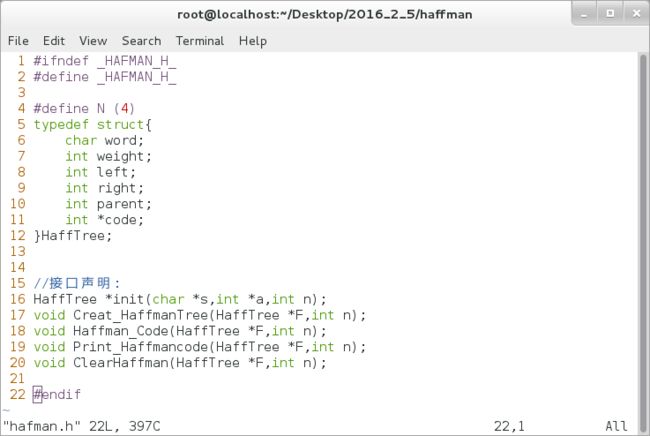
1)存储结构:
word weight left right parent code
A 9 -1 -1 -1
B 2 -1 -1 -1
C 7 -1 -1 -1
D 4 -1 -1 -1
定义存储结构:
下面实现接口:
#include <stdio.h>
#include <stdlib.h>
#include "hafman.h"
#include "tools.h"
HaffTree *init(char * s,int * a,int n)
{
HaffTree *F = {0};
int i = 0;
F = (HaffTree *)Malloc(((2 * n) - 1) * sizeof(HaffTree));
for(i = 0;i < n;i++){
F[i].word = s[i];
F[i].weight = a[i];
F[i].left = -1;
F[i].right = -1;
F[i].parent = -1;
}
return F;
}
void Creat_HaffmanTree(HaffTree *F,int n)
{
int i = 0;
int k1 = 0;
int k2 = 0;
int j = 0;
for(i = 0;i < n -1 ; ++i){
for(k1 = 0;k1 < n + i && F[k1].parent != -1;k1++);
for(k2 = k1 + 1;k2 < n + i && F[k2].parent != -1;k2++);
for(j = k2;j < n + i;j++){
if(F[j].parent == -1){
if(F[j].weight < F[k1].weight){
k2 = k1;
k1 = j;
}else if(F[j].weight < F[k2].weight){
k2 = j;
}
}
}
F[n + i].word = 'x';
F[n + i].weight = F[k1].weight + F[k2].weight;
F[n + i].left = k1;
F[n + i].right = k2;
F[n + i].parent = -1;
F[k1].parent = n + i;
F[k2].parent = n + i;
}
}
void Haffman_Code(HaffTree *F,int n)
{
int i = 0;
int c = 0;
int p = 0;
int k = 0;
for(i = 0;i < n;++i){
F[i].code = (int *)Malloc((n + 1) * sizeof(int));
F[i].code[0] = 0;
c = i;
while(F[c].parent != -1){
p = F[c].parent;
k = ++F[i].code[0];
if(F[p].left == c){
F[i].code[k] = 0;
}else{
F[i].code[k] = 1;
}
c = p;
}
}
}
void Print_Haffmancode(HaffTree *F,int n)
{
int i = 0;
int j = 0;
for(i = 0;i < n;++i){
printf("%c:",F[i].word);
for(j = F[i].code[0];j > 0;--j){
printf("%2d",F[i].code[j]);
}
printf("\n");
}
}
void ClearHaffman(HaffTree *F,int n)
{
int i = 0;
for(i = 0;i < n;++i){
free(F[i].code);
}
free(F);
}
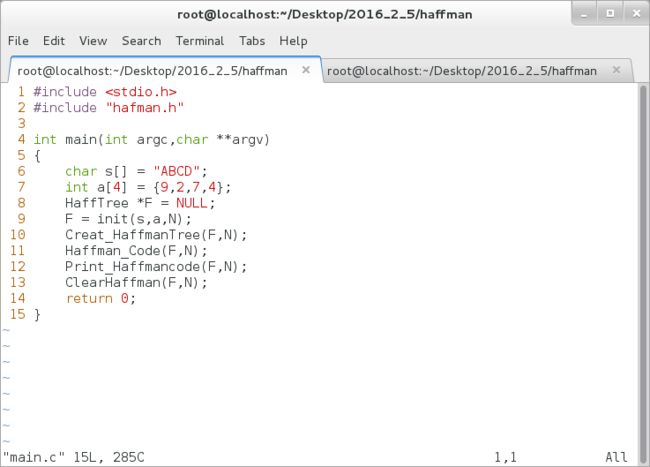
测试代码:
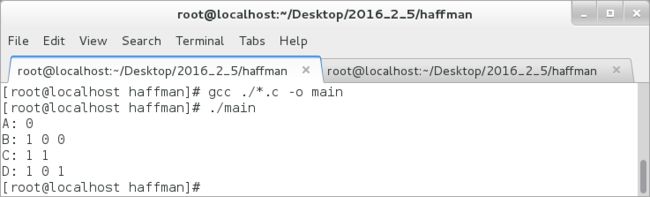
测试结果:
从程序执行结果上可看出实现了压缩数据,节省了空间。