Yale开放课程博弈论18

18. 信息集合和子博弈完美

 

回顾一下我们之前介绍的博弈论，我们先介绍了同步决策，即当我做决策时并不知道你会做什么决策，参与者同时做出决策。之后又介绍了序贯博弈，即参与者按照顺序做出决策，且我做决策之前能够知道你将会有那些应对策略。

而今天我们介绍的博弈中则会包含这两种情况。

 

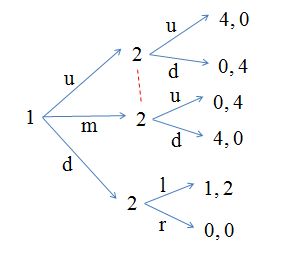
上图所示即为我们今天要介绍的一种博弈，它与之前唯一的不同在于中间出现了一条红色的虚线。现在我们引入“信息集合”的概念，即图中用虚线将上面两个2结点连在一起，表示参与者2在做决策的时候不清楚1选择的是u还是m，即虚线使得一些信息对于参与者来说是不清晰的，一些独立的决策变成了一些决策的集合。

上面图中的例子，参与者1会随机选择u或m（期望收益是2），而选择d的收益却是1。当把图中的虚线去掉，则由于参与者1根据逆向归纳法会选择d，因为若他选择u或者m，参与者2就会选择收益为(0, 4)，这样参与者1的收益为0，所以他会选择d，收益为1。

 

定义：

参与者i的信息集合，是一系列参与者i无法识别的结点。

不允许的一些事情：

1. 同一个信息集合中的点处的选择策略集合是一样的；

2. 参与者1只要知道自己之前的选择，就知道自己现在处于的结点（完美的记忆力）。

 

完美信息：（每个人都记得之前的决策）

树图上所有信息集合包含一个节点的博弈（所有元素都是单元素）

 

另外一个例子，参与者1有两个选择，参与者2有三个选择，参与者2处于信息集合中。我们可以把树转化成收益矩阵。再画一个树图（参与者2在前参与者1在后，参与者1处于信息集合中），我们得到的收益矩阵是一样的，2有三个选择，1有两个选择，2先做选择，1再做选择。

这两个博弈是一样的，即不论是1先行动还是2先行动，实际是没有影响的，因为后采取行动的参与者并不清楚对手的策略。

 

博弈中一个很重要的因素就是whatthey know, and when they know。

 

下面的一个例子说明有些纳什均衡不能在树图中通过逆向归纳法得到。

三个参与者的例子，参与者1可以选择A或者B，如果她选择A游戏结束，收益为1,0,0

如果参与者1选择B，则参与者2有两个选择，之后参与者3分别有两个选择。

 

可以画两个收益矩阵，分别对应参与者1选择A或者B时参与者2和3之间的收益。

如果参与者1选择B，则参与者2和3进入子博弈，只看他们两人的子博弈，在这个子博弈中，参与者3有一个优势策略，且该子博弈中只有一个纳什均衡（d, r）。

在收益矩阵中我们会得到这样一个均衡（A， u， l）（尽管参与者1选择A之后游戏会结束），子博弈中的均衡却是（d, r）。

 

子博弈是博弈的一部分，非正式的说法就是像树图里面的一个博弈

必须满足三个条件：

1. 子博弈必须从单个节点开始

2. 它包含该节点的所有后代节点

3. 不破坏任何信息集合

 

我们希望排除那些无法使参与者在子博弈中进入纳什均衡的纳什均衡。

 

纳什均衡，NE（s1*, s2*,..., sm*）如果它能在任一子博弈中达到纳什均衡，完美均衡（SPE， sub-game perfect equilibrium），则称为子博弈完美均衡。