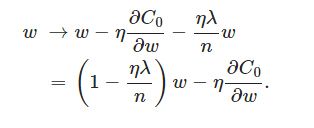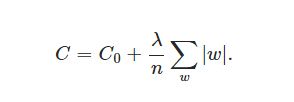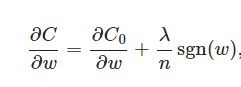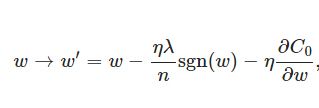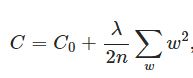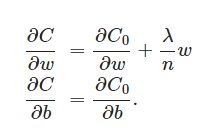机器学习：L1与L2正则化项

题目

关于支持向量机SVM,下列说法错误的是（）

  A. L2正则项，作用是最大化分类间隔，使得分类器拥有更强的泛化能力

  B. Hinge 损失函数，作用是最小化经验分类错误

  C. 分类间隔为1/||w||，||w||代表向量的模

  D. 当参数C越小时，分类间隔越大，分类错误越多，趋于欠学习(错误)

在Logistic Regression 中,如果同时加入L1和L2范数,会产生什么效果（）

  A. 可以做特征选择,并在一定程度上防止过拟合

  B. 能解决维度灾难问题

  C. 能加快计算速度

  D. 可以获得更准确的结果(正确答案)

----------------------------------------------------------------------------------------------

L1正则化和L2正则化

正则化项即罚函数，该项对模型向量进行“惩罚”，从而避免单纯最小二乘问题的过拟合问题。训练的目的是最小化目标函数，则C越小，意味着惩罚越小，分类间隔也就越小，分类错误也就越少。

正则化项本质上是一种先验信息，整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计的形式，如果你将这个贝叶斯最大后验估计的形式取对数，即进行极大似然估计，你就会发现问题立马变成了损失函数+正则化项的最优化问题形式。

(1) 避免出现过拟合（over-fitting）。经验风险最小化 + 正则化项 = 结构风险最小化。

(2) 从模型求解上看，正则化提供了一种唯一解的可能。光用最小二乘拟合可能出现无数组解，加个L1或L2正则化项能有唯一解。

L1范数是指向量中各个元素绝对值之和，用于特征选择; 

L2范数 是指向量各元素的平方和然后求平方根，用于 防止过拟合，提升模型的泛化能力

L1与L2区别：使用L1可以得到稀疏的权值；用L2可以得到平滑的权值

L1 regularization（往0方向靠）

在原始的代价函数后面加上一个L1正则化项，即所有权重w的绝对值的和，乘以λ/n（这里不像L2正则化项那样，需要再乘以1/2，具体原因上面已经说过。）

同样先计算导数：

上式中sgn(w)表示w的符号。那么权重w的更新规则为：

比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大

因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

L2 regularization（权重衰减）

L2正则化就是在代价函数后面再加上一个正则化项：

C0代表原始的代价函数，后面那一项就是L2正则化项，它是这样来的：所有参数w的平方的和，除以训练集的样本大小n。λ就是正则项系数，权衡正则项与C0项的比重。另外还有一个系数1/2，1/2经常会看到，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。

L2正则化项是怎么避免overfitting的呢？我们推导一下看看，先求导：

可以发现L2正则化项对b的更新没有影响，但是对于w的更新有影响.