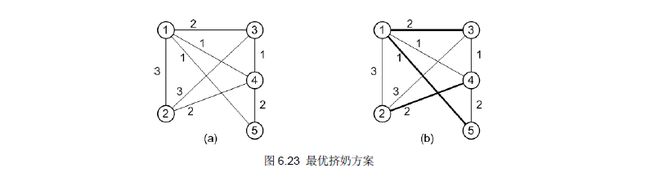
poj2112Optimal Milking(最优秀的挤奶方案)——floyd+最大流+二分

http://poj.org/problem?id=2112

题目描述：
农场主John 将他的K(1≤K≤30)个挤奶器运到牧场，在那里有C(1≤C≤200)头奶牛，在奶
牛和挤奶器之间有一组不同长度的路。K个挤奶器的位置用1～K的编号标明，奶牛的位置用K+1～
K+C 的编号标明。
每台挤奶器每天最多能为M(1≤M≤15)头奶牛挤奶。
编写程序，寻找一个方案，安排每头奶牛到某个挤奶器挤奶，并使得C 头奶牛需要走的所有
路程中的最大路程最小。每个测试数据中至少有一个安排方案。每条奶牛到挤奶器有多条路。

输入描述：
测试数据的格式如下：
第1 行为3 个整数K、C 和M。
第2～K+C+1 行，每行有K+C 个整数，描述了奶牛和挤奶器（二者合称实体）之间的位置，
这K+C 行构成了一个沿对角线对称的矩阵。第2 行描述了第1 个挤奶器离其他实体的距离，…，
第K+1 行描述了第K 个挤奶器离其他实体的距离；第K+2 行描述了第1 头奶牛离其他实体的距
离，…。这些距离为不超过200 的正数。实体之间如果没有直接路径相连，则距离为0。实体与
本身的距离（即对角线上的整数）也为0。

输出描述：
输出一个整数，为所有方案中，C 头奶牛需要走的最大距离的最小值。

因为题目要求路径里面最大的最小，所以先用floyd求得任意两点之间的最短路，然后二分枚举可能的最大边，根据所枚举的最大边的前提限制，建图，源点到各个奶牛的容量为1，各个牛奶站到汇点的容量为M，如果某个奶牛到奶牛站的距离小于等于所枚举的最大边，则容量为1，求得最大流是否等于C

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#define REP(i,n) for(int i=0;i<(n);++i)
#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define FORD(i,a,b) for(int i=(a);i<=(b);++i)
const int maxn=250;
const int INF=1<<30;
using namespace std;
int n,s,t;
int K,C,M;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
vector<Edge> edges;
vector<int> G[maxn];
int gap[maxn],d[maxn],cur[maxn],p[maxn];
inline void addedge(int u,int v,int c){
    edges.push_back(Edge(u,v,c,0));
    edges.push_back(Edge(v,u,0,0));
    int m=edges.size();
    G[u].push_back(m-2);
    G[v].push_back(m-1);
}
int ISAP(){
    s=0,t=n;
    memset(cur,0,sizeof(cur));
    memset(d,0,sizeof(d));
    memset(gap,0,sizeof(gap));
    int x=s,flow=0,a=INF;
    while(d[s]<n){
        if(x==t){
            flow+=a;
            while(x!=s){
                edges[p[x]].flow+=a;
                edges[p[x]^1].flow-=a;
                x=edges[p[x]].from;
            }
            a=INF;
        }
        int ok=0;
        for(int i=cur[x];i<G[x].size();++i){
            Edge& e=edges[G[x][i]];
            if(e.cap>e.flow&&d[e.to]+1==d[x]){
                p[e.to]=G[x][i];
                cur[x]=i;
                x=e.to;
                ok=1;
                a=min(a,e.cap-e.flow);
                break;
            }
        }
        if(!ok){
            int m=n;
            for(int i=0;i<G[x].size();++i){
                Edge& e =edges[G[x][i]];
                if(e.cap>e.flow) m=min(m,d[e.to]);
            }
            if(--gap[d[x]]==0) break;
            gap[d[x]=m+1]++;
            cur[x]=0;
            if(x!=s) x=edges[p[x]].from;
        }
    }
    return flow;
}



int g[maxn][maxn];
int maxh,maxedge;
void floyd(){
    maxh=-1;
    FORD(k,1,n)FORD(i,1,n){
        if(g[i][k]<INF)
        FORD(j,1,n){
            g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
            if(g[i][j]<INF) maxh=max(maxh,g[i][j]);
        }
    }
}
void build(int mid){
    maxedge=-1;
    edges.clear();
    for(int i=0;i<maxn;++i) G[i].clear();
    FORD(i,1,K) addedge(i,n,M);
    FORD(i,K+1,K+C) addedge(0,i,1);
    FORD(i,K+1,K+C){
        FORD(j,1,K){
            if(g[i][j]<=mid){
                addedge(i,j,1);
                maxedge=max(maxedge,g[i][j]);
            }
        }
    }
}
int main()
{
    cin>>K>>C>>M;
    n=K+C;
    FORD(i,1,n)FORD(j,1,n){
        scanf("%d",&g[i][j]);
        if(g[i][j]==0) g[i][j]=INF;
    }
    floyd();
    n+=2;
    int maxflow;
    int l=0,r=maxh;
    while(l<r){
        int mid=(l+r)>>1;
        build(mid);
        maxflow=ISAP();
        cout<<"Maxflow="<<maxflow<<endl;
        if(maxflow>=C) r=mid;
        else l=mid+1;
    }
    build(r);
    cout<<maxedge<<endl;
    return 0;
}