BZOJ 2119 股市的预测 后缀数组
题目大意:给定一个序列,求差分后有多少个子串满足形式为ABA,其中B部分长度为m,A部分长度大于0
首先枚举A的长度j,将序列上每隔j个点插入一个关键点
对于第i个位置上的关键点,我们找到第i+j+m个位置
利用后缀数组找出两个位置向左拓展多少个位置都是相同的,以及向右拓展都少个位置都是相同的
为了保证不重复向左和向右最多拓展j-1个位置
设拓展之后长度为len,那么如果len>=j,ans+=(len-j+1)
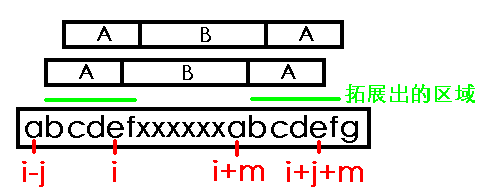
如图,拓展出的区域长度为5,j=4,则可以找到两个子串
其中两个a虽然相同,但是由于a属于上一个关键点,因此为了避免重复计数而不再向左拓展
总关键点数O(nlogn)时间复杂度O(nlogn)
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define M 100100
using namespace std;
int n,m,a[M];
int log2[M],min_height[M][18];
long long ans;
namespace Suffix_Array{
int sa[M],rank[M],height[M];
int X[M],Y[M],sum[M],temp[M],tot;
void Get_Rank(int n)
{
static pair<int,int> b[M];
int i;
for(i=1;i<=n;i++)
b[i]=make_pair(a[i],i);
sort(b+1,b+n+1);
for(i=1;i<=n;i++)
{
if( i==1 || b[i].first!=b[i-1].first )
++tot;
rank[b[i].second]=tot;
}
}
void Radix_Sort(int n,int key[],int order[])
{
int i;
for(i=0;i<=n;i++)
sum[i]=0;
for(i=1;i<=n;i++)
sum[key[i]]++;
for(i=1;i<=n;i++)
sum[i]+=sum[i-1];
for(i=n;i;i--)
temp[sum[key[order[i]]]--]=order[i];
for(i=1;i<=n;i++)
order[i]=temp[i];
}
void Get_Height(int n)
{
int i,j,k;
for(i=1;i<=n;i++)
{
if(rank[i]==1) continue;
j=max(height[rank[i-1]]-1,0);
k=sa[rank[i]-1];
while(a[i+j]==a[k+j])
++j;
height[rank[i]]=j;
}
}
void Prefix_Doubling(int n)
{
int i,j;
Get_Rank(n);
for(j=1;j<=n;j<<=1)
{
for(i=1;i<=n;i++)
{
X[i]=rank[i];
Y[i]=i+j>n?0:rank[i+j];
sa[i]=i;
}
Radix_Sort(n,Y,sa);
Radix_Sort(n,X,sa);
for(tot=0,i=1;i<=n;i++)
{
if( i==1 || X[sa[i]]!=X[sa[i-1]] || Y[sa[i]]!=Y[sa[i-1]] )
++tot;
rank[sa[i]]=tot;
}
}
Get_Height(n);
}
}
int Min_Height(int x,int y)
{
if(x>y) swap(x,y);
int len=log2[y-(++x)+1];
return min(min_height[x][len],min_height[y-(1<<len)+1][len]);
}
int main()
{
using namespace Suffix_Array;
int i,j;
cin>>n>>m;
memset(a,0xef,sizeof a);
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
for(n--,i=1;i<=n;i++)
a[i]=a[i+1]-a[i];
a[n+1]=19980402;
for(i=n;i;i--)
a[n+n+2-i]=a[i];
Prefix_Doubling(n+n+1);
for(log2[0]=-1,i=1;i<=n+n+1;i++)
log2[i]=log2[i>>1]+1;
for(i=1;i<=n+n+1;i++)
min_height[i][0]=height[i];
for(j=1;j<=log2[n+n+1];j++)
for(i=1;i+(1<<j)-1<=n+n+1;i++)
min_height[i][j]=min(min_height[i][j-1],min_height[i+(1<<j-1)][j-1]);
for(j=1;j+j+m<=n;j++)
{
int last=0;
for(i=1;i+j+m<=n;i+=j)
{
int temp=Min_Height(rank[i],rank[i+j+m]);
temp=min(temp,j);
if(last+temp>=j)
ans+=last+temp-j+1;
last=Min_Height(rank[(n+n+2)-(i+j-1)],rank[(n+n+2)-(i+j+j+m-1)]);
last=min(last,j-1);
}
}
cout<<ans<<endl;
return 0;
}