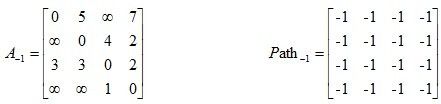Java数据结构----图--最短路径解法Dijkstra算法和Floyd算法
最短路径—Dijkstra算法和Floyd算法
1、Dijkstra算法
1.1、定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
1.2、算法描述
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图
代码实现如下:
public class GraphByMatrix {
public static final boolean UNDIRECTED_GRAPH = false;//无向图标志
public static final boolean DIRECTED_GRAPH = true;//有向图标志
public static final boolean ADJACENCY_MATRIX = true;//邻接矩阵实现
public static final boolean ADJACENCY_LIST = false;//邻接表实现
public static final int MAX_VALUE = Integer.MAX_VALUE;
private boolean graphType;
private boolean method;
private int vertexSize;
private int matrixMaxVertex;
//存储所有顶点信息的一维数组
private Object[] vertexesArray;
//存储图中顶点之间关联关系的二维数组,及边的关系
private int[][] edgesMatrix;
// 记录第i个节点是否被访问过
private boolean[] visited;
/**
* @param graphType 图的类型:有向图/无向图
* @param method 图的实现方式:邻接矩阵/邻接表
*/
public GraphByMatrix(boolean graphType, boolean method, int size) {
this.graphType = graphType;
this.method = method;
this.vertexSize = 0;
this.matrixMaxVertex = size;
if (this.method) {
visited = new boolean[matrixMaxVertex];
vertexesArray = new Object[matrixMaxVertex];
edgesMatrix = new int[matrixMaxVertex][matrixMaxVertex];
//对数组进行初始化,顶点间没有边关联的值为Integer类型的最大值
for (int row = 0; row < edgesMatrix.length; row++) {
for (int column = 0; column < edgesMatrix.length; column++) {
edgesMatrix[row][column] = MAX_VALUE;
}
}
}
}
/********************最短路径****************************/
//计算一个顶点到其它一个顶点的最短距离
public void Dijkstra(Object obj) throws Exception {
Dijkstra(getVertexIndex(obj));
}
public void Dijkstra(int v0) {
int[] dist = new int[matrixMaxVertex];
int[] prev = new int[matrixMaxVertex];
//初始化visited、dist和path
for (int i = 0; i < vertexSize; i++) {
//一开始假定取直达路径最短
dist[i] = edgesMatrix[v0][i];
visited[i] = false;
//直达情况下的最后经由点就是出发点
if (i != v0 && dist[i] < MAX_VALUE)
prev[i] = v0;
else
prev[i] = -1; //无直达路径
}
//初始时源点v0∈visited集,表示v0 到v0的最短路径已经找到
visited[v0] = true;
// 下来假设经由一个点中转到达其余各点,会近些,验证之
// 再假设经由两个点中转,会更近些,验证之,.....
// 直到穷举完所有可能的中转点
int minDist;
int v = 0;
for (int i = 1; i < vertexSize; i++) {
//挑一个距离最近经由点,下标装入 v
minDist = MAX_VALUE;
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && dist[j] < minDist) {
v = j; // 经由顶点j中转则距离更短
minDist = dist[j];
}
}
visited[v] = true;
/*顶点v并入S,由v0到达v顶点的最短路径为min.
假定由v0到v,再由v直达其余各点,更新当前最后一个经由点及距离*/
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && edgesMatrix[v][j] < MAX_VALUE) {
if (minDist + edgesMatrix[v][j] <= dist[j]) {
//如果多经由一个v点到达j点的 最短路径反而要短,就更新
dist[j] = minDist + edgesMatrix[v][j];
prev[j] = v; //经由点的序号
}
}
}
}
for (int i = 1; i < matrixMaxVertex; i++) {
System.out.println("**" + vertexesArray[v0] + "-->" +vertexesArray[i] + " 的最短路径是:" + dist[i]);
}
}
//获取顶点值在数组里对应的索引
private int getVertexIndex(Object obj) throws Exception {
int index = -1;
for (int i = 0; i < vertexSize; i++) {
if (vertexesArray[i].equals(obj)) {
index = i;
break;
}
}
if (index == -1) {
throw new Exception("没有这个值!");
}
return index;
}
/**
* 单源最短路径算法,用于计算一个节点到其他!!所有节点!!的最短路径
*/
public void Dijkstra2(int v0) {
// LinkedList实现了Queue接口 FIFO
Queue<Integer> queue = new LinkedList<Integer>();
for (int i = 0; i < vertexSize; i++) {
visited[i] = false;
}
//这个循环是为了确保每个顶点都被遍历到
for (int i = 0; i < vertexSize; i++) {
if (!visited[i]) {
queue.add(i);
visited[i] = true;
while (!queue.isEmpty()) {
int row = queue.remove();
System.out.print(vertexesArray[row] + "-->");
for (int k = getMin(row); k >= 0; k = getMin(row)) {
if (!visited[k]) {
queue.add(k);
visited[k] = true;
}
}
}
}
}
}
private int getMin( int row) {
int minDist = MAX_VALUE;
int index = 0;
for (int j = 0; j < vertexSize; j++) {
if ((!visited[j]) && edgesMatrix[row][j] < minDist) {
minDist = edgesMatrix[row][j];
index = j;
}
}
if (index == 0) {
return -1;
}
return index;
}
public boolean addVertex(Object val) {
assert (val != null);
vertexesArray[vertexSize] = val;
vertexSize++;
return true;
}
public boolean addEdge(int vnum1, int vnum2, int weight) {
assert (vnum1 >= 0 && vnum2 >= 0 && vnum1 != vnum2 && weight >= 0);
//有向图
if (graphType) {
edgesMatrix[vnum1][vnum2] = weight;
} else {
edgesMatrix[vnum1][vnum2] = weight;
edgesMatrix[vnum2][vnum1] = weight;
}
return true;
}
}
测试:
@Test
public void testWeight() throws Exception {
GraphByMatrix graph = new GraphByMatrix(Graph.UNDIRECTED_GRAPH, Graph.ADJACENCY_MATRIX, 6);
graph.addVertex("1");
graph.addVertex("2");
graph.addVertex("3");
graph.addVertex("4");
graph.addVertex("5");
graph.addVertex("6");
graph.addEdge(0, 1,7);
graph.addEdge(0, 2,9);
graph.addEdge(0, 5,14);
graph.addEdge(1, 3,15);
graph.addEdge(1, 2,10);
graph.addEdge(2, 3,11);
graph.addEdge(2, 5,2);
graph.addEdge(3, 4,6);
graph.addEdge(4, 5,9);
graph.Dijkstra(0);
System.out.println();
graph.Dijkstra("1");
System.out.println();
graph.Dijkstra2(0);
System.out.println();
}
**1-->2 的最短路径是:7
**1-->3 的最短路径是:9
**1-->4 的最短路径是:20
**1-->5 的最短路径是:20
**1-->6 的最短路径是:11
**1-->2 的最短路径是:7
**1-->3 的最短路径是:9
**1-->4 的最短路径是:20
**1-->5 的最短路径是:20
**1-->6 的最短路径是:11
1-->2-->3-->6-->4-->5-->
2、Floyd算法:读弗洛伊德
1.定义概览
Floyd-Warshall算法(Floyd-Warshall algorithm)又称为插点法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
2.算法描述:
1)算法思想原理:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
2).算法描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
3).Floyd算法过程矩阵的计算----十字交叉法
方法:两条线,从左上角开始计算一直到右下角 如下所示
给出矩阵,其中矩阵A是邻接矩阵,而矩阵Path记录u,v两点之间最短路径所必须经过的点
相应计算方法如下:
最后A3即为所求结果
代码如下: