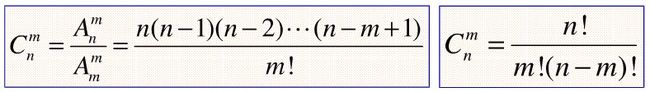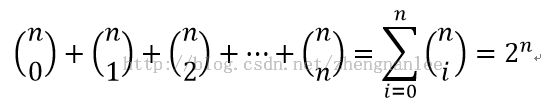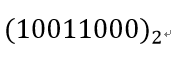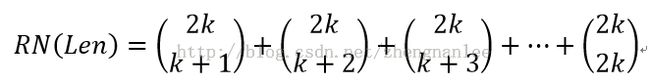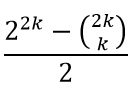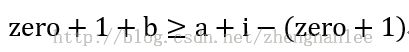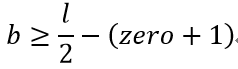poj 3252(细心+组合数溢出+边界条件计算+算上数据本身)

Round Numbers

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 7756		Accepted: 2674

Description

The cows, as you know, have no fingers or thumbs and thus are unable to play Scissors, Paper, Stone' (also known as 'Rock, Paper, Scissors', 'Ro, Sham, Bo', and a host of other names) in order to make arbitrary decisions such as who gets to be milked first. They can't even flip a coin because it's so hard to toss using hooves.

They have thus resorted to "round number" matching. The first cow picks an integer less than two billion. The second cow does the same. If the numbers are both "round numbers", the first cow wins,
otherwise the second cow wins.

A positive integer N is said to be a "round number" if the binary representation of N has as many or more zeroes than it has ones. For example, the integer 9, when written in binary form, is 1001. 1001 has two zeroes and two ones; thus, 9 is a round number. The integer 26 is 11010 in binary; since it has two zeroes and three ones, it is not a round number.

Obviously, it takes cows a while to convert numbers to binary, so the winner takes a while to determine. Bessie wants to cheat and thinks she can do that if she knows how many "round numbers" are in a given range.

Help her by writing a program that tells how many round numbers appear in the inclusive range given by the input (1 ≤ Start < Finish ≤ 2,000,000,000).

Input

Line 1: Two space-separated integers, respectively   Start  and   Finish.

Output

Line 1: A single integer that is the count of round numbers in the inclusive range   Start.. Finish

Sample Input

2 12

Sample Output

6

Source

USACO 2006 November Silver

下面参考Daze同学的博客分析并做了一些补充，写的非常好：

首先，

RoundNumber[start, end] = RoundNumber[0,start-1] - RoundNumber[0,end] 

《组合数学》第二章“排列与组合”中，阐述了几个原理：加法原理、减法原理、乘法原理。各自的前提是不同的，需要仔细去了解。

重点不在上面，上面只是基础。

首先在高中我们学过组合数的定义：

然后它具有以下常用性质：

1、

2、

3、（由分类计数证明，动态规划思想）

4.

性质3常用于打表，因为其具递推的性质。

切入正题，假设有如下二进制数：

问其是否是RoundNumber？答案是肯定的。

最一开始我们知道，要想求RN[start,end]，我们只需要求RN[0,start-1]-RN[0,end]。归根结底是求RN[0,x]。

这个问题转化思想非常重要，避免了同时考虑上下界。

把这个八位二进制数分情况讨论一下，比它小的分两种情况，一是1至7位数，二是八位数。

情况一：

一个二进制，长度为Len的数，若使0的个数大于1的个数，可以这么安排：

若Len是奇数，即Len=2*k+1，最高位是1，其余2k位（注意当规定一个数是len位的时候，最高位一定是1)，则有：

至此，Len是奇数时我们解决了。可以直接算这些组合数（从表中直接取，以下代码就是这么操作的），也可以利用一下上面提供的性质。由性质2知，在性质1和式函数中，最头的两个是对称相等的。那么，上式恰好等于：

若Len是偶数，Len=2*k，最高位是1，其余2k-1位，同理可得：

情况二：当位数为8时：

先放大一下这个二进制数：

可以清晰地看到，第四位，我标记了1。如果将1改为0，那么剩下的四位任意填数都满足该数（新的）小于这个二进制数(10011000)B。但是不能任意填，还是要满足0的个数大于1的个数，那么我们有如下结论：

令l为长度，i为当前改变的“1”的位置，如图中的位置4，zero为0的计数（绝对计数、不包含被改变的第四位数1），a为需要填数的位置（下图中的虚线框）中1的个数，b为需要填数的位置中0的个数。

有如下等式：

有如下不等式：

解得：

这个式子说明了，至少要填那么b个零，也就是l/2-(zero+1)。注意奇偶。至多呢？至多全填满呗。填多少？l-i个（空格数）呗。注意，程序中是从高位到地位搜索，i的位置表示的是绿色的1的位置，l-i是空格（虚线框）的个数。（如果这个觉得这个公式用脑力推比较复杂，实际竞赛中可以写一个循环去得到那个b）

实际运算中，给l先加1，然后整除2，方可。

至此，问题解决了，那么代码就很简单了。

提交记录：

1、WA 因为组合数计算的时候没有考虑 可能会溢出（即使用long long 也会溢出）（虽然结果肯定不会超过32位int，但中间计算结果可能会溢出！！切忌！！）

2、WA组合数计算中，用float保存中间结果，可能会 损失精度，因此改用double。（这里以后最好用 打表的方式吧。毕竟这么计算是有风险的）

3、WA计算上面分析段落中的 b计算错误（程序中是i）（一直在分奇数偶数讨论，始终讨论不正确），以后还是严格推导公式为好。

4、WA修改为严格推导后，可以看到cal函数中的i值计算法方法为：

    (num + numones + 1) / 2    

     这里括号里面加上1，其实就是 上取整的意思，以后需要奇数偶数分类讨论时，其实往往是需要上取整，直接 加上1整除2就可以完美解决。

    事实上， 正数的 整除运算 ‘/’ 就是 下取整，如果需要上取整操作就 先加1，再/2。

    而 负数正好相反，整除运算'/' 是 上取整。如果需要下取整操作，就 先减1，再/2。

5、WA上面计算出来的i可能是小于0的，而事实上i至少是0（也就是全部取1）。如果 i为负数带入C()函数计算组合数，会有意想不到的情况发生。

6、WA上面当最高位取0的时候，后面需要依次计算n-1次 RN，也就是RN(n-1), RN(n-2), RN(n-3) ...,  RN(1)   是一个循环，而不是一下子就可以计算出来。

7、WA在计算第二部分的值的时候，当遇到0的时候，要记得给ones减去1.否则逻辑上是错误的！

8、WA如果 数据本身是满足要求的ROUND NUM，要加1！因为前面分类讨论的过程中，并没有将数据本身计算在内。

9、Accepted。

WA哭了，写程序途中让我回想起了成都赛里面的F题，就是一道组合数学题，当时也WA哭了，细节太多，一定要细心。

代码：