第六周周赛——AK机会不易得，好好把握题解（出自HDU5650，codeforces 616A，624A，659A，655A，658A）
A题：
A题题目链接
题目描述：
位运算
已知一个包含 n 个元素的正整数集合S，设 f(S) 为集合S中所有元素的异或(XOR)的结果。
如：S={1,2,3}, 则 f(S) = 0。
给出集合S，你需要计算 将所有f(s)进行异或后的值, 这里 s⊆S.
多组测试数据。第一行包含一个整数T(T≤20) 表示组数。
每组测试数据第一行包含一个数 n(1≤n≤1,000) 表示集合的大小，第二行为 n个数表示集合
元素。第 i(1≤i≤n) 个数 0 ≤ai ≤1000,000,000 且数据保证所给集合中没有重复元素。
对于每组测试数据，输出一个数，表示将所有的 f(s)异或之后的值。
1 3 1 2 3
0
样例中，S={1,2,3}, 它的子集有∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}
这道题乍看上去让人摸不着头脑，其实却是一道非常简单的题目。一开始做题目没有头绪的时候，我们可以从简单枚举开始，从而
寻找一般规律。
首先，需要了解的是一些异或运算的基本性质：
异或的性质和运算
异或运算是满足结合律和交换律的，可以用卡诺图和真值表进行证明，这里就不细说了。
当集合S中只有一个元素的时候，子集只有空集和其本身。很明显，所有f(s)异或后的值就是其本身
当集合S中有两个元素{a1,a2}的时候，子集有空集，{a1}，{a2}，{a1，a2}。那么所有集合进行异或运算的结果即为：
a1 ^ a2 ^ a1 ^ a2 = a1 ^ a1 ^ a2 ^ a2 = 0
当集合S中有三个元素{a1,a2,a3}的时候，子集有空集，{a1}，{a2}，{a3}，{a1，a2}，{a1，a3}，{a2，a3}，{a1，a2，a3}。那么所
有集合进行异或运算的结果即为：
a1 ^ a2 ^ a3 ^ a1 ^ a2 ^ a1 ^ a3 ^ a2 ^ a3 ^ a1 ^ a2 ^ a3= a1 ^ a1 ^ a1 ^ a1 ^ a2 ^ a2 ^ a2 ^ a2 ^ a3 ^ a3^ a3 ^ a3 = 0
枚举到这里，因此我们可以猜想，集合S中元素个数大于1时，所有子集异或后的结果为0，否则则为其本身。
简单证明：
假设集合S中有n个元素，对于其中的任一元素x，则总共2^（n-1）个子集包含元素x(排列组合证明，这里不详细说，有兴趣的可
以自己证明，结合二项式定理)，那么当n>1时，x在所有子集中个数之和为偶数，那么所有x异或后的结果必为0，当n = 1时，则
特判只含有一个元素的情况。
完整代码实现：
#include<cstdio>
int main(){
int T,n,value;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
for(int i = 1;i <= n;++i){
scanf("%d",&value);
}
if(n==1){
printf("%d\n",value);
}
else{
printf("0\n");
}
}
}
B题：
B题题目链接
题目描述：
Comparing Two Long Integers
You are given two very long integers a, b (leading zeroes are allowed). You should check what number a or b is greater or determine that they are equal.
The input size is very large so don't use the reading of symbols one by one. Instead of that use the reading of a whole line or token.
As input/output can reach huge size it is recommended to use fast input/output methods: for example, prefer to usescanf/printf instead of cin/cout in C++, prefer to use BufferedReader/PrintWriter instead of Scanner/System.out in Java. Don't use the function input() in Python2 instead of it use the function raw_input().
The first line contains a non-negative integer a.
The second line contains a non-negative integer b.
The numbers a, b may contain leading zeroes. Each of them contains no more than 106 digits.
Print the symbol "<" if a < b and the symbol ">" if a > b. If the numbers are equal print the symbol "=".
9
10
<
11
10
>
00012345
12345
=
0123
9
>
0123
111
>
给定两个整数，这两个整数可能含有前缀0，然后比较这两个数的大小，输出相应符号(< > =)
解析：
用字符串处理，分三种情况，除去前缀0之后，长者更大，反之短者更小，同样长则调用strcmp函数判断。
完整代码实现：
#include <cstdio>
#include <cstring>
char s[1000001], t[1000001];
int main()
{
scanf("%s %s", s, t);
int n = 0, m = 0;
while (s[n] == '0')
n++;
while (t[m] == '0')
m++;
int l1 = strlen(s + n);
int l2 = strlen(t + m);
if (l1 < l2)
puts("<");
else if (l1 > l2)
puts(">");
else
{
int cmp = strcmp(s + n, t + m);
puts(cmp > 0 ? ">" : (cmp == 0 ? "=" : "<"));
}
return 0;
}
C题题目链接
题目描述：
Save Luke
Luke Skywalker got locked up in a rubbish shredder between two presses. R2D2 is already working on his rescue, but Luke needs to stay alive as long as possible. For simplicity we will assume that everything happens on a straight line, the presses are initially at coordinates 0 and L, and they move towards each other with speed v1 and v2, respectively. Luke has width d and is able to choose any position between the presses. Luke dies as soon as the distance between the presses is less than his width. Your task is to determine for how long Luke can stay alive.
The first line of the input contains four integers d, L, v1, v2 (1 ≤ d, L, v1, v2 ≤ 10 000, d < L) — Luke's width, the initial position of the second press and the speed of the first and second presses, respectively.
Print a single real value — the maximum period of time Luke can stay alive for. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 
.
2 6 2 2
1.00000000000000000000
1 9 1 2
2.66666666666666650000
Note
In the first sample Luke should stay exactly in the middle of the segment, that is at coordinates [2;4], as the presses move with the same speed.
In the second sample he needs to occupy the position 
. In this case both presses move to his edges at the same time.
两个人分别从A,B两地相向而行，当两个人的距离达到d时，停止运动，问此时两个人运动的时间，距离L，两人速度v1，v2均给出。
解析：
相遇问题，列个一元一次方程求解即可
完整代码实现：
#include<cstdio>
int main(){
int d,L,v1,v2;
while(scanf("%d %d %d %d",&d,&L,&v1,&v2)==4){
printf("%.20f\n",double(L-d)/(v1+v2));
}
return 0;
}
D题：
D题题目链接
Round House
Vasya lives in a round building, whose entrances are numbered sequentially by integers from 1 to n. Entrance n and entrance 1 are adjacent.
Today Vasya got bored and decided to take a walk in the yard. Vasya lives in entrance a and he decided that during his walk he will move around the house b entrances in the direction of increasing numbers (in this order entrance n should be followed by entrance 1). The negative value of b corresponds to moving |b| entrances in the order of decreasing numbers (in this order entrance 1 is followed by entrance n). If b = 0, then Vasya prefers to walk beside his entrance.
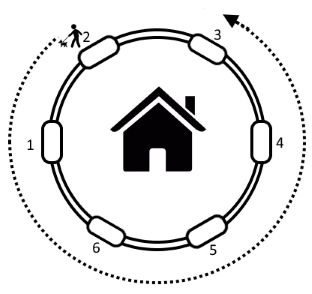Illustration for n = 6, a = 2, b = - 5.
Help Vasya to determine the number of the entrance, near which he will be at the end of his walk.
The single line of the input contains three space-separated integers n, a and b (1 ≤ n ≤ 100, 1 ≤ a ≤ n, - 100 ≤ b ≤ 100) — the number of entrances at Vasya's place, the number of his entrance and the length of his walk, respectively.
Print a single integer k (1 ≤ k ≤ n) — the number of the entrance where Vasya will be at the end of his walk.
6 2 -5
3
5 1 3
4
3 2 7
3
Note
The first example is illustrated by the picture in the statements.
给定n，a，b分别表示入口的个数，初始位置以及要走过的路口数，b值为负时逆时针走动，否则则顺时针走动。问最后走到的路口
的标号。
解析：
直接模拟题意即可，注意防止标号为负。
完整代码实现：
#include<cstdio>
int main(){
int n,a,b;
while(scanf("%d %d %d",&n,&a,&b)==3){
printf("%d\n",(a+100*n+b)%n ? (a+100*n+b)%n : n);
}
return 0;
}
E题：
E题题目链接
题目描述：
Amity Assessment
Bessie the cow and her best friend Elsie each received a sliding puzzle on Pi Day. Their puzzles consist of a 2 × 2 grid and three tiles labeled 'A', 'B', and 'C'. The three tiles sit on top of the grid, leaving one grid cell empty. To make a move, Bessie or Elsie can slide a tile adjacent to the empty cell into the empty cell as shown below:
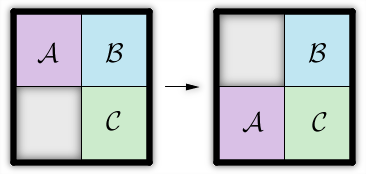
In order to determine if they are truly Best Friends For Life (BFFLs), Bessie and Elsie would like to know if there exists a sequence of moves that takes their puzzles to the same configuration (moves can be performed in both puzzles). Two puzzles are considered to be in the same configuration if each tile is on top of the same grid cell in both puzzles. Since the tiles are labeled with letters, rotations and reflections are not allowed.
The first two lines of the input consist of a 2 × 2 grid describing the initial configuration of Bessie's puzzle. The next two lines contain a 2 × 2 grid describing the initial configuration of Elsie's puzzle. The positions of the tiles are labeled 'A', 'B', and 'C', while the empty cell is labeled 'X'. It's guaranteed that both puzzles contain exactly one tile with each letter and exactly one empty position.
Output "YES"(without quotes) if the puzzles can reach the same configuration (and Bessie and Elsie are truly BFFLs). Otherwise, print "NO" (without quotes).
AB
XC
XB
AC
YES
AB
XC
AC
BX
NO
Note
The solution to the first sample is described by the image. All Bessie needs to do is slide her 'A' tile down.
In the second sample, the two puzzles can never be in the same configuration. Perhaps Bessie and Elsie are not meant to be friends after all...
给定两个2*2的宫格，问左边的宫格通过若干次移动之后，是否能够移成右边宫格的形状。
解析：
由于宫格只有2*2，直接暴力模拟即可。
完整代码实现：
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
string a[2], b[2];
int main()
{
cin >> a[0] >> a[1] >> b[0] >> b[1];
for (int i = 0; i < 1000; ++i) {
if (a[0] == b[0] && a[1] == b[1]) {
cout << "YES";
return 0;
}
if (a[0][0] == 'X') swap(a[0][0], a[0][1]);
else if (a[0][1] == 'X') swap(a[0][1], a[1][1]);
else if (a[1][1] == 'X') swap(a[1][1], a[1][0]);
else if (a[1][0] == 'X') swap(a[1][0], a[0][0]);
}
cout << "NO";
return 0;
}
F题：
F题题目链接
题目描述：
Bear and Reverse Radewoosh
Limak and Radewoosh are going to compete against each other in the upcoming algorithmic contest. They are equally skilled but they won't solve problems in the same order.
There will be n problems. The i-th problem has initial score pi and it takes exactly ti minutes to solve it. Problems are sorted by difficulty — it's guaranteed that pi < pi + 1 and ti < ti + 1.
A constant c is given too, representing the speed of loosing points. Then, submitting the i-th problem at time x (x minutes after the start of the contest) gives max(0, pi - c·x) points.
Limak is going to solve problems in order 1, 2, ..., n (sorted increasingly by pi). Radewoosh is going to solve them in ordern, n - 1, ..., 1 (sorted decreasingly by pi). Your task is to predict the outcome — print the name of the winner (person who gets more points at the end) or a word "Tie" in case of a tie.
You may assume that the duration of the competition is greater or equal than the sum of all ti. That means both Limak and Radewoosh will accept all n problems.
The first line contains two integers n and c (1 ≤ n ≤ 50, 1 ≤ c ≤ 1000) — the number of problems and the constant representing the speed of loosing points.
The second line contains n integers p1, p2, ..., pn (1 ≤ pi ≤ 1000, pi < pi + 1) — initial scores.
The third line contains n integers t1, t2, ..., tn (1 ≤ ti ≤ 1000, ti < ti + 1) where ti denotes the number of minutes one needs to solve the i-th problem.
Print "Limak" (without quotes) if Limak will get more points in total. Print "Radewoosh" (without quotes) if Radewoosh will get more points in total. Print "Tie" (without quotes) if Limak and Radewoosh will get the same total number of points.
3 2
50 85 250
10 15 25
Limak
3 6
50 85 250
10 15 25
Radewoosh
8 1
10 20 30 40 50 60 70 80
8 10 58 63 71 72 75 76
Tie
Note
In the first sample, there are 3 problems. Limak solves them as follows:
- Limak spends 10 minutes on the 1-st problem and he gets 50 - c·10 = 50 - 2·10 = 30 points.
- Limak spends 15 minutes on the 2-nd problem so he submits it 10 + 15 = 25 minutes after the start of the contest. For the 2-nd problem he gets 85 - 2·25 = 35 points.
- He spends 25 minutes on the 3-rd problem so he submits it 10 + 15 + 25 = 50 minutes after the start. For this problem he gets 250 - 2·50 = 150 points.
So, Limak got 30 + 35 + 150 = 215 points.
Radewoosh solves problem in the reversed order:
- Radewoosh solves 3-rd problem after 25 minutes so he gets 250 - 2·25 = 200 points.
- He spends 15 minutes on the 2-nd problem so he submits it 25 + 15 = 40 minutes after the start. He gets 85 - 2·40 = 5 points for this problem.
- He spends 10 minutes on the 1-st problem so he submits it 25 + 15 + 10 = 50 minutes after the start. He gets max(0, 50 - 2·50) = max(0, - 50) = 0 points.
Radewoosh got 200 + 5 + 0 = 205 points in total. Limak has 215 points so Limak wins.
In the second sample, Limak will get 0 points for each problem and Radewoosh will first solve the hardest problem and he will get 250 - 6·25 = 100 points for that. Radewoosh will get 0 points for other two problems but he is the winner anyway.
In the third sample, Limak will get 2 points for the 1-st problem and 2 points for the 2-nd problem. Radewoosh will get 4 points for the 8-th problem. They won't get points for other problems and thus there is a tie because 2 + 2 = 4.
由于在题目后方，题意已经解释得非常清楚，因此题意不再多说。其实这就是codeforces本地比赛的规则（codeforces daily 、
round），因此在处理从前往后做题和从后往前做题的两种情况时，我们分别可以用后缀和以及前缀和先预处理一下即可。
完整代码实现：
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = int(1e3) + 10;
int p[maxn],t[maxn],t1[maxn],t2[maxn];
int main(){
int n,c;
while(scanf("%d %d",&n,&c)==2){
for(int i = 1;i <= n;++i){
scanf("%d",&p[i]);
}
for(int i = 1;i <= n;++i){
scanf("%d",&t[i]);
t1[i] = t[i];
t2[i] = t[i];
}
for(int i = 1;i < n;++i){
t1[i+1] += t1[i];
}
for(int i = n;i > 1;--i){
t2[i-1] += t2[i];
}
int score1 = 0,score2 = 0;
for(int i = 1;i <= n;++i){
score1 += max(0,p[i]-c*t1[i]);
}
for(int i = n;i >= 1;--i){
score2 += max(0,p[i]-c*t2[i]);
}
if(score1 > score2){
printf("Limak\n");
}
else if(score1 < score2){
printf("Radewoosh\n");
}
else{
printf("Tie\n");
}
}
return 0;
}
如有错误，还请指正，O(∩_∩)O谢谢