用 JAVA 开发游戏连连看（之二）实现游戏的算法

（之二）实现游戏的算法

将游戏地图转换为数组来描述

算法总是很枯燥的，没有直接设计界面来得舒服，然而，算法却是整个程序的核心，所以，仅管枯燥，我们还是得耐心地完成这一步。

在进行程序算法的设计时，我们首先要尽可能抛开一些无关紧要的部分，这样可以使算法看起来直接明了，但同时也要考虑弹性，以便将来扩充。

在前面已经说过了，整个游戏的核心算法也就是以二维数组为主体的算法，那么，定义一个二维数组是必不可少的了。

二维数组究竟应该有多大呢？ 10X10 是不是小了， 20*20 呢，大了？究竟多大比较合适？为了考虑到程序以后改动的需要，我们还是定义成变量吧，这样以后要改动的时候，只需要改动一下变量的值就行了，因此，我们现在为程序增加一个类，使之专门用来保存与程序有关的一些数据。

//Setting.java

public static final int ROW = 8; // 假设地图有 8 行

public static final int COLUMN = 8; // 假设地图有 8 列


至于为什么要定义成 public static final ，这个，自己想想就知道了：）还不知道？晕，看看书吧：（

现在，我们将这个类起名为 Map ，同时，我们规定，为了描述地图中空白的区域，我们使用 0 来表示。

//Map.java

private int[][] map = new int[Setting.ROW][Setting.COLUMN];


初始化游戏地图

在地图初始化的时候，我们需要用一些“随机”的数字来填充这张地图，之所有将“随机”用引号括起来，是因为这些数字并不是真正意义上的随机：首先，数组中具有相同值的元素只能出现 4 次（具有 0 值的元素除外），其次，这些数字是被散乱的分布在数组中的。

要使元素出现 4 次，那么数组中所有不重复的元素个数最大为数组的大小 /4 ，为了简单起先，我们使这些元素的值用 1 、 2 、 3 ……进行编号。

要想将这些分配好的元素再分配到二维数组中，我们需要一个一维数组来辅助完成这项工作。

首先，我们按照二维数组的大小来建立一个大小相同的一维数组，并且，我们规定数组中出现的不重复的元素的个数（元素个数的多少代表了地图的填充率，填充率越高，表示游戏难度越高），同时，我们也要保证数组的长度能被 4 整除（目前是这样，其实不是必需的），因为相同的元素会出现 4 次。因此，我们定义一个变量，用来表示地图上可能出现元素种类的最大个数，同时也定义一个变量，表示目前地图上出现的元素的个数。

//Map.java

int[] array = new int[Setting.ROW * Setting.COLUMN]; // 辅助的一维数组

int maxElement = 16; //maxElement 的值不能超过 map 总元素 /4

int elements = 16; // 先假设 maxElement 和 elements 相等


在，我们将这些元素放置在一维数组中：

for (int i = 0; i < max; i++) {

array[i * 4] = i + 1;

array[i * 4 + 1] = i + 1;

array[i * 4 + 2] = i + 1;

array[i * 4 + 3] = i + 1;

}


这时，一维数组初始化完成了，可惜数组中的元素是规规矩矩按顺序出现的，如果不打乱就填充到地图中，这游戏似乎也太简单了（因为相邻的点一定可以消除啊），现在，我们得想个办法打乱这个数组。

怎么打乱这个数组呢？好办，我们来看看，假设数组的原始排列是这样的：

[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

从最后一个元素 [15] 起，依次与此元素之前的某一个元素将值互换，完成后再从 [14] 起，与在 [14] 之前的某一个元素将值互换，直到 [1] 与 [0] 的值互换后，如此一来，数组就被完全打乱了，如果还不明白，我们来看一看下图：

[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

在 [15] 之前有 15 个元素，产生一个 15 以内的随机数，比如说 8 ，再将 [15] 和 [8] 的值互换，变成了如下：

[0] [1] [2] [3] [4] [5] [6] [7] [15] [9] [10] [11] [12] [13] [14] [8]

再从 [14] 号元素开始，产生一个 14 以内的随机数，比如说 10 ，互换 [14] 和 [10] 的值：

改变前：

[0] [1] [2] [3] [4] [5] [6] [7] [15] [9] [10] [11] [12] [13] [14] [8]

改变后：

[0] [1] [2] [3] [4] [5] [6] [7] [15] [9] [14] [11] [12] [13] [10] [8]

怎么样，略施小技就搞定了，简单吧？算法如下：

int[] random(int[] array) {

java.util.Random random = new java.util.Random();

for (int i = array.length; i > 0; i--) {

int j = random.nextInt(i);

int temp = array[j];

array[j] = array[i - 1];

array[i - 1] = temp;

}

return array; // 其实也可以不返回，因为数组的操作总是改变引用的

}


现在，一维数组中的元素已经被打乱了，现在我们只需要按顺序依次填充回二维数组中就行了，这样，二维数组中的值就一定是乱的。

for (int i = 0; i < ROW; i++) {

for (int j = 0; j < COLUMN; j++) {

map[j] = array[i * COLUMN + j];

}

}



( 打乱后的数组，感觉如何，虽然难看了点，但很有用 )

对数组中两个元素是否可以消除的判断

地图的初始化已经完成了，现在的问题是，我们怎么样才能知道数组中的两个元素是否可以消除呢？

根据游戏规则，如果两个点之间可以用不超过 3 条直线连接起来，这两点就可以消除，现在我们来分析一下所有可能的情况：

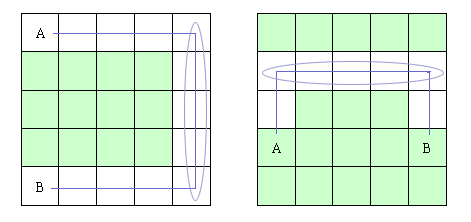
两点之间只需要一条直线连接：

(图略了……)

由上图可以看出，如果两点间只需要一条直线能够连接起来，则 A 、 B 两点的横坐标或纵坐标必定相同，有了这个条件，我们判断 A 、 B 两点是否只需要一条直接连接就简单了许多。

这段代码比较简单，所以就不写出来了，大家可以看看源程序，只不过需要注意的是，我们将横线连接和竖线连接分开来处理，这样做是为了后面工作的简单。

boolean verticalMatch(Point a, Point b) // 竖线上的判断

boolean horizonMatch(Point a, Point b) // 横线上的判断


( 注意：为了简单省事，我们用 java.awt 包中的 Poin(x, y)t 来描述二维数组中元素的坐标，但是有一点要特别小心， x 和 y 与二维数组中元素的下标值 恰好相反 ，如左上图中 A 的下标为 array[1][0] ， Point 的描述却是为 Point(0, 1) ，如果不注意这一点，程序会出错的。 )

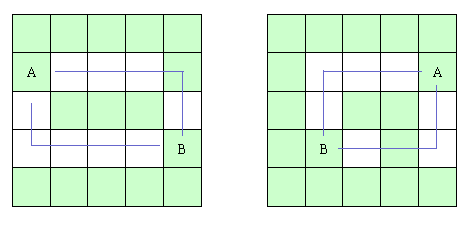
两点之间需要两条直线连接：



如上图， A 、 B 两点如果需要两条直线连接起来，有可能有两种方式，于是，我们可以巧妙的构建一个 C 点和一个 D 点，并且规定 C 点的横坐标为 A 点的横坐标， C 点的纵坐标为 B 点的纵坐标， D 点的横坐标为 B 点的横坐标， D 点的纵坐标为 A 点的纵坐标（这一点很重要，因为 C 、 D 决定了 AC 、 BC 、 AD 、 BD 的连线方式），如下图：



如果此时 C 点（或 D 点）能同时满足 AC （ AD ）、 BC （ BD ）只需要一条直线相连，就表示 A 、 B 之前能够使用两条直线连接起来，并且 C 点（ D 点）为拐点（以后会用上的）

//A 、 B 之间有一个拐点

boolean oneCorner(Point a, Point b) {

Point c, d;

boolean isMatch;

c = new Point(a.x, b.y);

d = new Point(b.x, a.y);

if (map[c.x][c.y] == 0) { //C 点上必须没有障碍

isMatch = horizonMatch(a, c) && verticalMatch (b, c);

if (isMatch) {

return isMatch;

}

}

if (map[d.x][d.y] == 0) { //D 点上必须没有障碍

isMatch = verticalMatch (a, d) && horizonMatch (b, d);

return isMatch;

}

return false;

}


( 注意：由于 C 点和 D 点的构建方式确定了 AC 、 BD 永远是竖连线、 BC 、 AD 永远是横连线 )

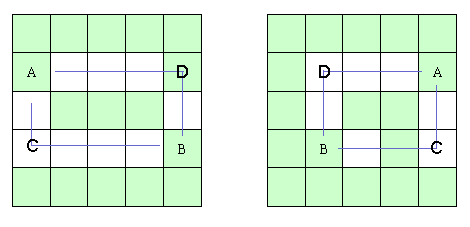
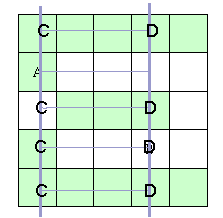
两点之间需要三条直线连接：

这种方式是最复杂的了，我们还是先分析一下出现三条直线的所有可能性吧。



( 图 A)



( 图 B ：这种方式比较容易忽略掉 )



以上图说明了两点间三条直线的所有可能性，和二条直线的情况相比，拐点是两个，麻烦了一点，但也不难处理。

下面我们来分析一下该怎么处理二个拐点的情况（三条直线）。由上面的图可以看出， A 、 B 如果要通过三条直线相连，则必须有 C 、 D 两个拐点，如果能确定下 C 、 D ，问题就好解决多了。

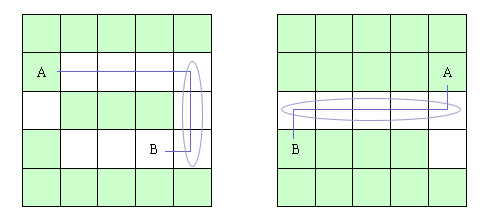
怎么样来确定 C 、 D 两点呢？我们以图 A 中的左图为例，在此之前，我们规定 C 点与 A 点在同一竖线上， D 点与 A 点在同一直线上。同时，从图中我们也可以看出， A 、 B 两点间如果只能通过三条直线连接起来，则必定有一条直线处于 A 、 B 的横向夹线纵向夹线中（如画圈的线）。

我们假设相等的线为在 A 、 B 两点的横坐标相等、纵坐标为 0~Setting.ROW 构成的区域上 ( 如图 ) 。

我们先扫描出所有的线，并且我们发现，如果在 A 、 B 构成的区域中存在两个点能构成直线，那么，这条直线就 有可能 是我们需要的直线，我们称此线为符合线，如果符合线的两端（ C 、 D 两点）与 A 、 B 两点分别能 AC 、 CD 、 DB 能构成直线的原则，则 AB 间一定可以通过三条直线连接起来。（这个可能我描述得不太清楚，但相信你应该不难明白的）

我们把所有找到的符合线保存起来，并且要记录下符合线是横向上的还是纵向上的，然后通过这些找到的符合线，依次和 A 、 B 两点进行判断，一旦找到这样的 C 、 D 两点，能满足 AC 、 CD 、 DB 这三条线上都没有障碍，那么， A 、 B 就可以消除了。还是用算法来描述一下吧。

首先我们构建一个保存 C 、 D 点的类 Line ，并且要指明 C 、 D 的方向是横向还是纵向。

//Line.java

public class Line {

public Point a, b;

public int direct; //1 表示横线， 0 表示竖线

public Line() {

}

public Line(int direct, Point a, Point b) {

this.direct = direct;

this.a = a;

this.b = b;

}

}


同时，由于在扫描的过程中，会找到多根符合线，因此，我们可以用 Vector 来保存这些找到的符合线（为了提高效率，也可以使用 LinkedList 来保存）。

Vector vector = new Vector(); // 保存求解后的线

扫描两点构成的矩形内有没有完整的空白线段

Vector scan(Point a, Point b) {

Vector v = new Vector();

// 从 a, c 连线向 b 扫描，扫描竖线

// 扫描 A 点左边的所有线

for (int y = a.y; y >= 0; y--) {

if (map[a.x][y] == 0 && map[b.x][y] == 0 &&

verticalMatch(new Point(a.x, y), new Point(b.x, y))) { // 存在完整路线

v.add(new Line(0, new Point(a.x, y), new Point(b.x, y)));

}

}

// 扫描 A 点右边的所有线

for (int y = a.y; y < COLUMN; y++) {

if (map[a.x][y] == 0 && map[b.x][y] == 0 &&

verticalMatch(new Point(a.x, y), new Point(b.x, y))) { // 存在完整路线

v.add(new Line(0, new Point(a.x, y), new Point(b.x, y)));

}

}

// 从 a, d 连线向 b 扫描，扫描横线

// 扫描 A 点上面的所有线

for (int x = a.x; x >= 0; x--) {

if (map[x][a.y] == 0 && map[x][b.y] == 0 &&

horizonMatch(new Point(x, a.y), new Point(x, b.y))) {

v.add(new Line(1, new Point(x, a.y), new Point(x, b.y)));

}

}

// 扫描 A 点下面的所有线

for (int x = a.x; x < ROW; x++) {

if (map[x][a.y] == 0 && map[x][b.y] == 0 &&

horizonMatch(new Point(x, a.y), new Point(x, b.y))) {

v.add(new Line(1, new Point(x, a.y), new Point(x, b.y)));

}

}

return v;

}


现在，我们对所有找到的符合线进行判断，看看 AC 、 DB 是否同样也可以消除

boolean twoCorner(Point a, Point b) {

vector = scan(a, b);

if (vector.isEmpty()) { // 没有完整的空白线段，无解

return false;

}

for (int index = 0; index < vector.size(); index++) {

Line line = (Line) vector.elementAt(index);

if (line.direct == 1) { // 横线上的扫描段，找到了竖线

if (verticalMatch(a, line.a) && verticalMatch(b, line.b)) { // 找到了解，返回

return true;

}

}

else { // 竖线上的扫描段，找到了横线

if (horizonMatch(a, line.a) && horizonMatch(b, line.b)) {

return true;

}

}

}

return false;

}




消除该两个元素时，只需要将两个元素的值置为 0 即可。

更多的功能：自动寻找匹配的点

现在，算法基本上是实现了，但是，为了使游戏更丰富，我们还需要实现更多的功能，现在，我们添加一个自动寻找匹配的点的功能。

该功能需要分两步走：

第一步，从左上向右下搜索二维数组中第一个值不为 0 的元素 A ，找到该点后，然后再从该点向后找到一个值与该点值相等的元素 B ，然后对这两个元素进行是否可消除的判断，如果可以消除，则说明该两点匹配，如果不能消除，则继续寻找与 A 点值相等的 B 点，如果找不到 B 点，则寻找下一个 A 点，依次下去，直到找不到这个 A 点，这就表时地图上已经不存在可消除的点了，我们用伪算法描述如下：

找到第一个 A 点

while (A 点存在时 ) {

while ( 能找到与 A 点值相等的 B 点 ) {

if (Match(A, b)) {

返回找到的 AB 点 ;

}

}

寻找下一个 A 点 ;

}

找不到点 ;


更多的功能：刷新地图

刷新地图的功能其实非常简单，只是需要将二维数组中现有的元素打乱后然后放回这个二维数组中就行了，我们还是只简单的用伪算法描述一下吧：）

找到地图中所有的值不为 0 的点并且保存到一维数组中

打乱一维数组

重新分配回二维数组中


完成代码并且测试

现在，算法部分的代码大体上算是完成了，我们可以进行一下测试，测试应该很简单，限于篇幅的原因，我就不在这里写出测试用的代码了，但可以说明一下如何进行测试：

我们可以构建一些特殊的地图，然后用 Match(Point a, Point b) 方法来判断我们指定的两点是否可以消除，或者使用自动寻找的功能，找到相同的两点后，消除这两个点，当地图上没有可消除的点时，就刷新地图，直到点全部消除完成。同时，我们还可以在 horzionMatch(Point a, Point b) 、 verticalMatch(Point a, Point b) 等加上输出语句，来看看匹配时程序执行到哪了，换几个不同的点多测试几次，如果没有问题，那就应该没有问题了：）