双调欧几里得旅行商问题【sicily 1163 && poj 2677.Tour】
题目链接:http://soj.me/1163
问题描述:由于旅行商问题是NP问题,所有J.L.Bentley建议只考虑双调旅程来简化问题。这种旅程即为从最左点开始,严格地从左到右直至最右点,然后严格地从右到左直至出发点。
分析:由于旅行商问题都是要求访问所有的点一遍而不重复,这里又对路径有个双调的约束,所以其实可以把问题看成是两个人同时从第一个点出发,中间分别经过不同的点(路径没有交集,但是要经过所有点),然后在最后一个点汇合,求两人路径之和的最小值。
本文中假设有n个点p1、p2、p3……pn,且n个点已按x坐标排好序。
解题思路:总体思想是动态规划,而且易知答案具有对称性(即第一个人从1走到i,第二个人从1走到j和第二个人从1走到i,第一个人从1走到j是一样的),而且除了第一个点和最后一个点,它们的路径不相交,所以只考虑i > j的情况。
状态:设dp[i, j]表示第一个人走到i,第二个人走到j(1<=j<i)时他们路径之和的最小值,这时从p1到pmax(i, j)上的点都已经经过了。
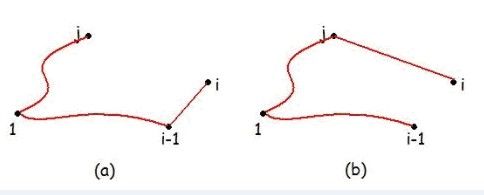
由上图可知,在状态dp[i-1,j]时(j < i-1),可以有两种状态转移方式:
1. 如(a)图,dp[i][j] = dp[i-1][j] + dist[i-1][i];(j<i-1)
2. 如(b)图,dp[i][i-1] = min(dp[i-1][k] + dist[k][i]) (1<=k<i-1)
注意这里解释一下这两种情况为什么这样转移。
首先看(a), 这种情况下,只能从i-1牵一条线到i,而不能是其它点,而且它是dp[i][j]的最小值。
再看(b),这种情况下,为什么不是dp[i-1][j] + dist[j][i],而要是min(dp[i-1][k] + dist[k][i]),我们可以这样想,我们从k(k<j)牵一条线到i,那么这样就等价于把p1-pk定位一条路线,其它的所有点都归到另一条路线,而这时的这种情况的值为dp[i-1][k] + dist[k][i],这种情况有可能比 dp[i-1][j] + dist[j][i]小。
最后,由于两条路径一定会在pn点汇合,所以,n点一定会和n-1点相连,那么我们可以通过dp[n][n-1] + dist[n][n-1]得到最终结果。
代码如下:
#include <cstdio>
#include <cstring>
#include <cmath>
#define N 105
#define INF 1000000000
struct Point
{
double x, y;
}p[N];
double dp[N][N], d[N][N];
//path用于记录一边的路径(或来或去)
//int path[N];
inline double dist(const Point& p1, const Point& p2)
{
return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}
//void print_path(int n)
//{
// if(n == 1)
// {
// printf("1 ");
// return;
// }
// print_path(path[n]);
// printf("%d ", n);
//}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
for(int i=1; i<=n; ++i)
scanf("%lf %lf", &p[i].x, &p[i].y);
for(int i=1; i<=n; ++i)
for(int j=1; j<i; ++j)
d[i][j] = dist(p[i], p[j]), dp[i][j] = INF;
dp[2][1] = d[2][1];
/*path[2] = 1;*/
for(int i=3; i<=n; ++i)
{
for(int j=1; j<i-1; ++j)
dp[i][j] = dp[i-1][j] + d[i][i-1];
double tmp;
for(int k=1; k<i-1; ++k)
{
tmp = dp[i-1][k] + d[i][k];
if(tmp < dp[i][i-1])
{
dp[i][i-1] = tmp;
/*path[i] = k;*/
}
}
}
printf("%.2lf\n", dp[n][n-1] + d[n][n-1]);
/*printf("The one-side path: ");
print_path(n);
printf("\n");*/
}
return 0;
}