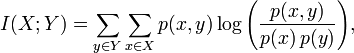Mutual information and Normalized Mutual information 互信息和标准化互信息
From: http://www.cnblogs.com/ziqiao/archive/2011/12/13/2286273.html
实验室最近用到nmi( Normalized Mutual information )评价聚类效果,在网上找了一下这个算法的实现,发现满意的不多.
浙江大学蔡登教授有一个,http://www.zjucadcg.cn/dengcai/Data/code/MutualInfo.m ,他在数据挖掘届地位很高,他实现这个算法的那篇论文引用率高达三位数。但这个实现,恕个人能力有限,我实在是没有看懂:变量命名极为个性,看的如坠云雾;代码倒数第二行作者自己添加注释why complex,我就更不懂了;最要命的是使用他的函数MutualInfo(L1,L2)得到的结果不等于MutualInfo(L2,L1),没有对称性!
还有个python的版本http://blog.sun.tc/2010/10/mutual-informationmi-and-normalized-mutual-informationnmi-for-numpy.html,这个感觉很靠谱,作者对nmi的理解和我是一样的。
我的理解来自wiki和stanford,其实很简单,先说一下问题:例如stanford中介绍的一个例子:
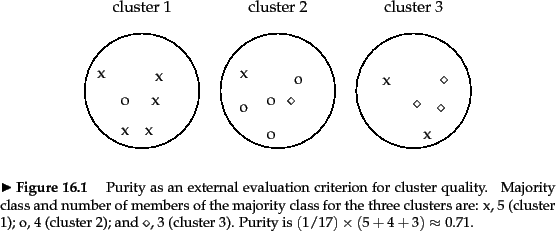
比如标准结果是图中的叉叉点点圈圈,我的聚类结果是图中标注的三个圈。
或者我的结果: A = [1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3];
标准的结果 : B = [1 2 1 1 1 1 1 2 2 2 2 3 1 1 3 3 3];
问题:衡量我的结果和标准结果有多大的区别,若我的结果和他的差不多,结果应该为1,若我做出来的结果很差,结果应趋近于0。
MI可以按照下面的公式计算。X=unique(A)=[1 2 3],Y=unique(B)=[1 2 3];
分子p(x,y)为x和y的联合分布概率,
p(1,1)=5/17, p(1,2)=1/17, p(1,3)=0;
p(2,1)=1/17, p(2,2)=4/17, p(2,3)=1/17;
p(3,1)=2/17, p(3,2)=0, p(3,3)=3/17;
分母p(x)为x的概率函数,p(y)为y的概率函数,x和y分别来自于A和B中的分布,所以即使x=y时,p(x)和p(y)也可能是不一样的。
对p(x): p(1)=6/17 p(2)=6/17 p(3)=5/17
对p(y): p(1)=8/17 p(2)=5/17 P(3)=4/17
这样就可以算出MI值了。
标准化互聚类信息也很简单,有几个不同的版本,大体思想都是相同的,都是用熵做分母将MI值调整到0与1之间。一个比较多见的实现是下面所示:
H(X)和H(Y)分别为X和Y的熵,下面的公式中log的底b=2。
例如H(X) = -p(1)*log2(p(1)) - -p(2)*log2(p(2)) -p(3)*log2(p(3))。