数据结构和算法12 之希尔排序
本文为博主原创文章,转载请注明出处: http://blog.csdn.net/eson_15/article/details/51168467
上一章我们学习了冒泡排序、选择排序和插入排序三种基础排序算法,这三种排序算法比较简单,时间复杂度均为O(N2),效率不高。这节我们讨论一个高级排序算法:希尔排序。希尔排序是基于插入排序的,插入排序有个弊端,假设一个很小的数据项在很靠近右端的位置上,那么所有的中间数据项都必须向右移动一位,这个步骤对每一个数据项都执行了将近N次的复制,这也是插入排序效率为O(N2)的原因。
希尔排序的中心思想是将数据进行分组,然后对每一组数据进行插入排序,在每一组数据都有序后,再对所有的分组利用插入排序进行最后一次排序。这样可以显著减少数据交换的次数,以达到加快排序速度的目的。
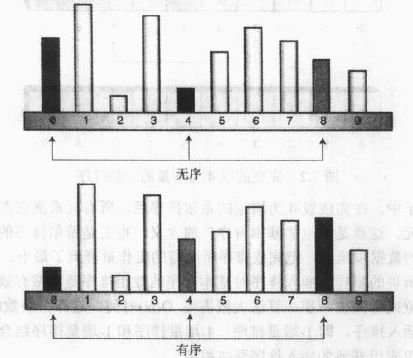
这种思想需要依赖一个增量序列,我们称为n-增量,n表示进行排序时数据项之间的间隔,习惯上用h表示。为了很好的理解增量排序,我们看下面的示意图:
上图显示了增量为4时对10个数据项进行排序的示意图,一趟后0、4、8三个位置上的数据项已经排好序,接下来,算法向右移动一步,对1、5、9三个位置的数据项进行排序,这个过程一直持续进行,直到所有数据项都完成了一次4-增量排序,然后缩小增量,再重复上面的过程,最后一次增量为1,对所有的数据项进行一次插入排序,从而完成了希尔排序的全部步骤。因为最后一趟都已经基本有序了,所以复杂度没有向普通插入排序那么大了。
说到这里,大家应该可以明白,增量序列在希尔排序中是很重要的。一般好的增量序列都有2个共同的特征:
1. 最后一个增量必须为1,保证最后一趟是一次普通的插入排序;
2. 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况
这篇文章中我们使用增量序列用 h = 3 * h + 1来生成。h初值被赋予1,然后使用该公式生成序列1、4、13、40、121、364等等,当间隔大于数组大小的时候停止,使用序列的最大数组作为间隔开始希尔排序过程,然后没完成一次排序,用倒推公式 h = (h - 1) / 3来减小间隔,保证最后一次h=1,完成最后一次插入排序。
说完了原理,下面看看具体实现代码:
public void shellSort2() {
int h = 1;
while(h <= nElem / 3) {
h = h * 3 + 1; //增量间隔
}
while(h > 0) {
for(int i = h; i < nElem; i++) {
//每个增量间隔内,实现插入排序,两个for循环和插入排序一样,只不过第二个for循环里参数略有调整而已,和h有关
for(int j = i; j < nElem; j += h) {
for(int k = j; (k - h >= 0) && a[k] < a[k - h]; k -= h) {
swap(k, k-h);
}
}
}
h = (h-1) / 3;
}
}
算法分析:希尔排序时间复杂度最好情况O(N),平均为O(NlogN),最坏情况O(N1.5)或O(N2)。对于不同的增量序列有不同的复杂度。希尔排序的性能优于直接插入排序,因为在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来随着增量逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但是由于已经局部排过序了,所以已经接近有序状态,新的一趟排序过程也较快。因此,希尔排序在效率上较直接插入排序有较大的改进。空间复杂度为O(1)。 希尔排序就介绍到这,如有错误之处,欢迎留言指正~
_____________________________________________________________________________________________________________________________________________________
-----乐于分享,共同进步!