纹理分析
参考自：
1. 引言
纹理是对图象的象素灰度级在空间上的分布模式的描述，反映物品的质地，如粗糙度、光滑性、颗粒度、随机性和规范性等。当图象中大量出现同样的或差不多的基本图象元素（模式）时，纹理分析是研究这类图象的最重要的手段之一，此外分形方法也十分重要[2]。
描述一块图象区域的纹理有三种主要的方法，统计分析方法、结构分析方法和频谱分析方法[1]。
统计方法有自相关函数、纹理边缘、结构元素、灰度的空间共生概率（spatial gray-tone cooccurrence probabilities）、灰度行程和自回归模型。统计方法将纹理描述为光滑、粗糙、粒状等等。
结构方法研究基元及其空间关系。基元一般定义为具有某种属性而彼此相连的单元的集合，属性包括灰度、连通区域的形状、局部一致性等。空间关系包括基元的相邻性、在一定角度范围内的最近距离等等。根据基元间的空间联系，纹理可以分为弱纹理或强纹理。进一步细分，可以根据基元的空间共生频率来划分，也可以根据单位面积内的边缘数来区别。基元也可以定义为灰度行程。
频谱方法是根据傅立叶频谱，根据峰值所占的能量比例将图象分类。包括计算峰值处的面积、峰值处的相位、峰值与原点的距离平方、两个峰值间的相角差等手段。
2. 纹理的统计特征
· 共生矩阵
共生矩阵用两个位置的象素的联合概率密度来定义，它不仅反映亮度的分布特性，也反映具有同样亮度或接近亮度的象素之间的位置分布特性，是有关图象亮度变化的二阶统计特征。它是定义一组纹理特征的基础。
如下图所示，定义位置算子：
假设给定如下的仅具有3个灰度级的图象区域，分别记数符合上述位置算子的象素空间组合的数目形成频度矩阵，再将其归一化，即除以符合位置关系的总数就得到共生矩阵。共生矩阵的阶数与图象的灰度级别数相等。
 |
 |
 |
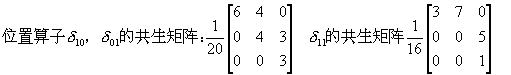· 基于共生矩阵的纹理特征
选择合适的位置算子，计算出共生矩阵，然后可以计算如下的纹理描述特征：
3. 基于纹理的分割
将图象分割成一些具有某种一致性的区域是图象分析的重要手段，一致性包括亮度、颜色或纹理等衡量标准。在机器视觉系统中，通常图象可以根据亮度标准进行分割，但在复杂的情况下，如自然景物，这种方法不能达到令人满意的分割效果。因为这类图象不具有均匀的亮度分布，而具有共同的纹理特征。
图片来自Extraction of Textured Regions
如果在没有任何先验知识以及任何统计训练数据可以利用的情况下，可以采用如下的基于共生矩阵的纹理分割方法。
例如，对于256x256大小的原图象，随机地选择40个NxN子图象，N需要根据实验来确定。记图象的灰度级数目是G，根据这些子图象计算各自的共生矩阵（GxG）。然后，将共生矩阵分成n等份方形子矩阵，用子矩阵元素的平均值形成一n维特征向量。根据它们在Rn特征空间的聚类情况，将图象分成不同的纹理区域。
在纹理分析中，Gabor变换是一种常用的重要工具，具有十分重要的作用。有关Gabor变换的基本概念在第12章第5节有介绍，更为深入的内容读者可以参照网上的相关资料（Gabor Filters for Texture (links) ..\..\download_IPCVPR\textureanalysis\USC Gabor Filters for Texture.htm）。
此外，分形技术在图象纹理分割中具有十分重要的应用，参见：杨波 徐光佑 朱志刚，基于分形特征的自然景物图象分割方法，中国图象图形学报，1999。