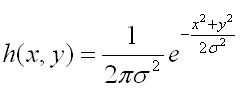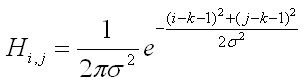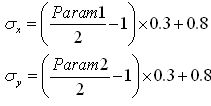高斯图像滤波原理及其编程离散化实现方法

转载地址：http://blog.csdn.net/likezhaobin/article/details/6835049

1、图像滤波

        在三维计算机视觉领域，通常对于二维图像的特征抽取是很关键的第一步，这主要包括抽取二维图像上的边缘、角点、纹理等。通常从这些被称为基元图的组成部分中，我们可以提取图像的以下特征：

        1）不同物体边缘成像所带来的灰度跃变；

        2）物体不同材料或者不同颜色组成部分之间的分界线会产生灰度跃变；

        3）物体轮廓线与背景具有不同的反射特性，也会形成灰度值不连续；

        4）物体受到光照会形成阴影，这也会形成层灰度的跃变。

       从上面分析可以看出，如果能够较好的从二维图像中提取出这些信息，那么对于三维重建，物体定位，空间监控等后期目标能够有很好的支撑作用。而这些含有图像轮廓以及空间位置信息的点、线、面等特征，在图像上都体现为灰度值的不连续或者剧烈变化。也就是说，如果我们能够根据图像灰度矩阵找到灰度不连续的点位置，那么也就是实现了特征抽取。

        不失一般性，从最简单的一维信号回忆，如果我们想从一维信号中找到其不连续的点，那么根据高等数学内容，可以对信号求导，其一阶导数局部最大值即为信号剧烈变化的点。

        在二维函数中，梯度向量代表着函数的最大变化率方向，因此对于二维信号，可以采用其梯度向量的模来选取灰度值不连续点。这样在理想情况下，我们就可以用离散化的梯度逼近函数来检测图像灰度矩阵的灰度跃变位置，从而实现特征抽取。

        现实中，有摄像机获取的图像，往往都存在噪声，而且信号并不存在理想的阶跃畸变，这样如果依然直接采用拉普拉斯算子进行灰度跃变检测，那样会产生很多的虚假特征点。因此，往往在图像处理之前，需要对灰度图进行滤波处理。

2、高斯滤波原理

           高斯滤波是最常用的一种图像滤波方法，本文就要对这种滤波的思路以及具体的编程实现原理进行挖掘整理。

2.1噪声的特性总结

       通常信息处理系统的目标是从测量到的带有噪声的信号中提取出真实的有用的信息，而往往真实有用信息是不可知的，因此只能通过滤波的方法进行信息估计。

       在我们进行数学仿真或者误差评估是，往往认为传感器所引入的噪声服从正态分布（高斯白噪声），这样我们在进行滤波的时候就可以有针对性的来进行滤波器设计。

2.2滤波通俗理解

       滤波就是根据观测某一随机过程的结果，对另一与之有关的随机过程进行估计的概率理论与方法。更通俗点讲，滤波就是建立的一个数学模型，通过这个模型来将图像数据进行能量转化，而能量低的就排除掉，噪声就是属于低能量部分。

       通常从传感器所获得的数据都是离散的，常用的图像滤波方法都是根据像素点附近邻域像素的灰度值进行相应的加权平均所得（经过实际检验，通过这样，可以有效的消除近似白噪声的噪声信号，对于图像滤波来说，这会使得图像边缘相比滤波前模糊一点），不同的滤波方法这个权值大小以及所加权的数据范围不同。

2.3 高斯滤波

       引入高斯滤波函数为：

                  

       该函数各向同性，其曲线是草帽状的对称图，该曲线对整个覆盖面积求积分为1。高斯滤波的思路就是：对高斯函数进行离散化，以离散点上的高斯函数值为权值，对我们采集到的灰度矩阵的每个像素点做一定范围邻域内的加权平均，即可有效消除高斯噪声。

3、高斯滤波离散化算法实现

       可以发现很多教材以及网上的资料都描述高斯滤波的原理是采用高斯算子对图像进行卷积运算。其实在各个算法库如Matlab、OpenCV等，在实现的时候，就是采用一个矩阵模板进行加权运算，拿图像的八连通区域来说，中间点的像素值就等于八连通区的像素值的均值，这样达到平滑的效果，该模板我们常成为高斯核。

       根据上述分析可知，高斯核是整个求解的关键。很显然，它是通过二维高斯函数计算得来的。这里给出离散高斯核矩阵的计算公式。

       离散的高斯卷积核H： (2k+1)×(2k+1)维，其元素计算方法为：

       其中Sigma为方差，k确定核矩阵的维数，关于这两个取值，在下文进行分析。

4、与matlab函数运行结果对比

      这里对高斯卷积核的矩阵算法进行验证。

      1）在matlab中用以下代码可以产生一个3×3的核。

                                               filter=fspecial('gaussian',3,1);

      所产生的核矩阵为：

                                   filter =

                                              0.0751    0.1238   0.0751

                                              0.1238    0.2042   0.1238

                                              0.0751   0.1238    0.0751

      2）同样对于上述的公式，我们取k=1，Sigma=1，即可得到3×3的高斯卷积核如下：

      

      上文说到，我们进行加权滤波，权系数之和必须为1，上面所求出的高斯滤波核函数同样的必须进行归一化：

       

      由此可以证明该核函数计算方法的正确性。

5、OpenCv中cvSmooth函数的用法

      该函数原型为：

                 void cvSmooth(const CvArr* src, CvArr* dst,

                              int smoothtype=CV_GAUSSIAN,

                              int param1=3, int param2=0,double param3=0, double param4=0 );

      该函数前三个参数很容易理解，至于后四个参数以下进行分析。

      1） 如果指定param1和param2，则代表核函数的行列，即为滤波窗口的宽度和高度；

      2） Param3：高斯卷积的Sigma值

      3） 如果用户希望采用非对称的高斯核，则引入param4，最后两个参数分别代表水平核以及垂直核维数；

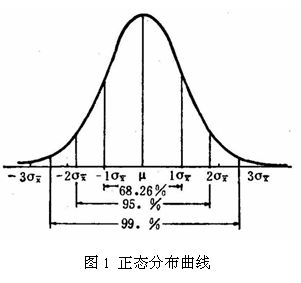
      4） 如果param3没有给出，则有前两个参数param1和param2计算出Sigma。这里的根据是高斯分布的特点（如图所示，数值分布在（μ—3σ,μ+3σ)中的概率为0.9974），如果核矩阵更大，那么相应的Sigma也更大，相反，如果Sigma更大，那么核矩阵覆盖范围也更大。具体到OpenCv下，用如下公式进行计算(根据其源代码显示)。

  

      5）同样的根据这个公式可知，如果param1和param2为0（或者没有给出），那么滤波窗口的尺寸，则有后两个参数代表的Sigma来确定。

    

6、总结

      本文主要整理了本人最近几天学习的心得体会，主要包括对滤波的理解，对高斯滤波方法原理以及实现过程的初窥。同时对采用OpenCV进行滤波实现的函数也给出了相应的解释。在此还要再说一下，在选择Sigma时要注意，如果选的过大，那么会加深滤波程度，这样会导致图像边缘模糊，不利于下一步的边缘检测，如果过小，则滤波效果不佳，对于该参数的选取目前本人也没什么较好的理解，在此引出问题，希望大家共同探讨进步。

参考资料：

[1] http://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83

[2]http://www.opencv.org.cn/index.php/Cv%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86

[3] http://www.cnblogs.com/donj/articles/1656122.html

[4]学习OpenCV中文版

[5]计算机视觉（马颂德版）