（1.2.5.2）二叉树遍历算法的应用

中心：利用递归思想，分为左右子树分别计算

（1）二叉树的创建：创建一颗二叉树，可以创建先序二叉树，中序二叉树，后序二叉树。我们在创建的时候为了方便，不妨用‘ ’表示空节点
（2）二叉树的节点个数：空返0；else 树中的节点的个数 = 左子树中节点的个数 + 右子树节点的个数+1跟。
（3）二叉树某节点所在层数：  递归查找查找，lev++
（4）二叉树的深度：空返0；叶子返1；else 树的高度 = max(左子树的高度，右子树的高度) + 1 
（5）二叉树的叶子节点个数：空返0；叶子返1；else 树中的叶子节点的个数 = 左子树中叶子节点的个数 + 右子树中叶子节点的个数
（6）完全二叉树的验证：层次遍历；
第一步：如果遍历到一个节点只有右子树没有左子树，则不是完全二叉树
第二步：如果遍历到一个节点只有左子树，或没有子树，那么后面遍历到的节点必须是叶子节点，否则也不是完全二叉树
（7）判断一个节点是否在子树中：递归遍历查找
（8）求两个节点的公共祖先：（1）如果两个节点同时在根节点的右子树中，则最近公共祖先一定在根节点的右子树中。（2）如果两个节点同时在根节点的左子树中，则最近公共祖先一定在根节点的左子树中。（3）如果两个节点一个在根节点的右子树中，一个在根节点的左子树中，则最近公共祖先一定是根节点。当然，要注意的是：可能一个节点pNode1在以另一个节点pNode2为根的子树中，这时pNode2就是这两个节点的最近公共祖先了。
（9）交换二叉树的左右儿子：先交换根节点的左右儿子节点，然后递归以左右儿子节点为根节点继续进行交换
（10）二叉树的宽度：
        算法1：层次遍历实现，定义length为0-n的自减，记录每层个数=queue.size();   max始终记录最大值
        算法2：递归实现： 每一个节点都导致下层的a[I]++ ；从左回右的时候 i--回退
（11）二叉树的节点的最大距离

（1）二叉树的创建

创建一颗二叉树，可以创建先序二叉树，中序二叉树，后序二叉树。我们在创建的时候为了方便，不妨用‘ ’表示空节点

先序创建

 int create(btree $bt){
 scanf(&ch);
 if(ch=='') T=Null;
 else
 {
    if(!T=(BTNode *)malloc(sizeof(BTNode)))
     exit;
    T->data=ch;
    Create(T->Lchild);
    Create(T->Rlchild);
 }
 return 1；
 }

（2）二叉树的节点个数

树中的节点的个数 = 左子树中节点的个数 + 右子树节点的个数+1跟。

  int BinTree::get_num(BinTreeNode *r)const
 {
     if(r == NULL)//该节点是空节点，比如建树时候用'#'表示
    {
          return 0;
     }
     else{//递归整个树的叶子节点个数 = 左子树叶子节点的个数 + 右子树叶子节点的个数
     return 1+get_num(r->get_left()) + get_num(r->get_right());
     }
 }

（3）二叉树某节点所在层数

  int BinTree::Find_LeveNum(BinTreeNode *r,BinTreeNode *x)const
 {
 if(r != NULL){
     lev++;
     if(r == x)//找到该节点
     {
           return lev;
      }
     else{
    Find_LeveNum(r->get_left())；
Find_LeveNum(r->get_right());
     }
   }
 }

（4）二叉树的深度

求二叉树的高度也是非常简单，不用多说：树的高度 = max(左子树的高度，右子树的高度) + 1 。

//获得二叉树的高度
int BinTree::get_tree_height(BinTreeNode *r)const
{
    if(r == NULL)//节点本身为空
    {
        return 0;
    }
    if(r->get_left()==NULL && r->get_right()==NULL)//叶子节点
    {
        return 1;
    }
    int l_height = get_tree_height(r->get_left());
    int r_height = get_tree_height(r->get_right());
    return l_height >= r_height ? l_height + 1 : r_height + 1; 
}

（5）二叉树的叶子节点个数

树中的叶子节点的个数 = 左子树中叶子节点的个数 + 右子树中叶子节点的个数。利用递归代码也是相当的简单，易懂。
1 //获取叶子节点的个数
 2 int BinTree::get_leaf_num(BinTreeNode *r)const
 3 {
 4     if(r == NULL)//该节点是空节点，比如建树时候用'#'表示
 5     {
 6         return 0;
 7     }
 8     if(r->get_left()==NULL && r->get_right()==NULL)//该节点并不是空的，但是没有孩子节点
 9     {
10         return 1;
11     }
12     //递归整个树的叶子节点个数 = 左子树叶子节点的个数 + 右子树叶子节点的个数
13     return get_leaf_num(r->get_left()) + get_leaf_num(r->get_right());
14 }

（6）完全二叉树的验证

可以使用层序遍历，只需2个步骤

第一步：如果遍历到一个节点只有右子树没有左子树，则不是完全二叉树

第二步：如果遍历到一个节点只有左子树，或没有子树，那么后面遍历到的节点必须是叶子节点，否则也不是完全二叉树

 //层序遍历
 int LayerOrder(BiTreeNode *head)
 {
     bool flag=0;
     LQueue Q;
     Initiate_Queue(&Q);
     BiTreeNode *p;
     if(head!=NULL) AppendQueue(&Q,head);
     while(QueueNotEmpty(&Q))
     {
         if(flag)  //标志位为1时，要保证后边全是叶子节点
         {
             if(p->LChild!=NULL || p->RChild!=NULL)
                 return 0;
         }
         p=QueueDelete(&Q);
         if(p->LChild!=NULL) AppendQueue(&Q,p->LChild);
         if(p->RChild!=NULL) AppendQueue(&Q,p->RChild);
         if((p->LChild==NULL) && (p->RChild!=NULL)) return 0;  //如果左子树为空，右子树存在，则不是完全2叉树
         //如果左子树存在，右子树为空，设置flag为1，进行进一步判断，判断后面遍历的节点是否为叶子节点
         if(p->LChild!=NULL &&p->RChild==NULL) flag=1;
         //如果左子树，右子树都为空，设置flag为1，进行进一步判断，判断后面遍历的节点是否为叶子节点
         if(p->LChild==NULL && p->RChild==NULL) flag=1;

     }
     return 1;
 }

（7）判断一个节点是否在子树中

可以和当前根节点相等，也可以在左子树或者右子树中。 

//判断一个节点t是否在以r为根的子树中
bool BinTree::is_in_tree(BinTreeNode *r,BinTreeNode *t)const
{
    if(r == NULL)
    {
        return false;
    }
    else if(r == t)
    {
        return true;
    }
    else
    {
        bool has = false;
        if(r->get_left() != NULL)
        {
            has = is_in_tree(r->get_left(),t);
        }
        if(!has && r->get_right()!= NULL)
        {
            has = is_in_tree(r->get_right(),t);
        }
        return has;
    }
}

（8）求两个节点的公共祖先

求两个节点的公共祖先可以用到上面的：判断一个节点是否在一颗子树中。（1）如果两个节点同时在根节点的右子树中，则最近公共祖先一定在根节点的右子树中。（2）如果两个节点同时在根节点的左子树中，则最近公共祖先一定在根节点的左子树中。（3）如果两个节点一个在根节点的右子树中，一个在根节点的左子树中，则最近公共祖先一定是根节点。当然，要注意的是：可能一个节点pNode1在以另一个节点pNode2为根的子树中，这时pNode2就是这两个节点的最近公共祖先了。显然这也是一个递归的过程啦：

//求两个节点的最近公共祖先
BinTreeNode* BinTree::get_nearest_common_father(BinTreeNode *r,BinTreeNode *pNode1,BinTreeNode *pNode2)const
{
    //pNode2在以pNode1为根的子树中（每次递归都要判断，放在这里不是很好。）
    if(is_in_tree(pNode1,pNode2))
    {
        return pNode1;
    }
    //pNode1在以pNode2为根的子树中
    if(is_in_tree(pNode2,pNode1))
    {
        return pNode2;
    }
    bool one_in_left,one_in_right,another_in_left,another_in_right;
    one_in_left = is_in_tree(r->get_left(),pNode1);
    another_in_right = is_in_tree(r->get_right(),pNode2);
    another_in_left = is_in_tree(r->get_left(),pNode2);
    one_in_right = is_in_tree(r->get_right(),pNode1);
    if((one_in_left && another_in_right) || (one_in_right && another_in_left))  //(3)
    {
        return r;
    }
    else if(one_in_left && another_in_left)                                    //（2）
    {
        return get_nearest_common_father(r->get_left(),pNode1,pNode2);
    }
    else if(one_in_right && another_in_right)
    {
        return get_nearest_common_father(r->get_right(),pNode1,pNode2);       //(1)
    }
    else
    {
        return NULL;
    }
}

可以看到这种做法，进行了大量的重复搜素，其实有另外一种做法，那就是存储找到这两个节点的过程中经过的所有节点到两个容器中，然后遍历这两个容器，第一个不同的节点的父节点就是我们要找的节点啦。 实际上这还是采用了空间换时间的方法。

（9）交换二叉树的左右儿子

交换二叉树的左右儿子，可以先交换根节点的左右儿子节点，然后递归以左右儿子节点为根节点继续进行交换。树中的操作有先天的递归性。

void BinTree::swap_left_right(BinTreeNode *r)
{
    if(r == NULL)
    {
        return;
    }
    BinTreeNode *pTmpNode = r->get_left();
    r->set_left(r->get_right());
    r->set_right(pTmpNode);
    swap_left_right(r->get_left());
    swap_left_right(r->get_right());
}

（10）二叉树的宽度

层次遍历实现，定义length为0-n的自减，记录每层

public static int findWidth(Node root)
{
int maxwidth = 1,length=0; //maxwidth 维持一个变量为最大宽度，length表示当前层的宽度
Node tmp;
if(root==null)
return 0;
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while(!queue.isEmpty())
{
   if(length==0)//每次length为0的时候，表示上层结束，进入新的一层，队列中为该层的宽度
   length = queue.size();
  if(length>maxwidth)//比较最大值
  maxwidth=length;
  while(length-->0)
   {
    tmp = queue.poll();
    if(tmp.left!=null)
    queue.add(tmp.left);
    if(tmp.right!=null)
    queue.add(tmp.right);
   }
}
return maxwidth;
}

递归法   每一个节点都导致下层的a[I]++

typedef struct node{
 char data;
 struct node *lchild,*rchild;
}NODE;
int a[10]={0};
int i=0;
void breadth(NODE *t)
{
 if(t!=NULL)
 {
  if(i==0)  //初始值的特殊情况
  {
   a[0]=1;
   i++;
   if(t->lchild!=NULL) a[i]++;
   if(t->rchild!=NULL) a[i]++;
  }
  else{  //正常情况
   i++;
   if(t->lchild!=NULL) a[i]++;
   if(t->rchild!=NULL) a[i]++;
  }
  breadth(t->lchild);  //左子树
  i--;                 //回退
  breadth(t->rchild);  //右子书
 }
}

（11）二叉树的节点的最大距离

解法一

根据相距最远的两个节点一定是叶子节点这个规律，我们可以进一步讨论。

对于任意一个节点，以该节点为根，假设这个根有K个孩子结点，那么相距最远的两个节点U和V之间的路径与这个根节点的关系有两种情况：

1.      若路径经过根Root，则U和V是属于不同子树的，且它们都是该子树中道根节点最远的节点，否则跟它们的距离最远相矛盾。这种情况如图3-13所示：

2.      如果路径不经过Root，那么它们一定属于根的K个子树之一。并且它们也是该子树中相距最远的两个顶点。如图3-14中的节点A：

    

//*************************************
//题目：
//     求一棵二叉树中距离相差最远的两个结点之间的距离。
//     
//        
//思路：注意指针声明了一定要赋值，否则会报错。
//        方法一：递归法
//距离相差最远的两个结点，共有以下两种情况：
//(1)路径经过根结点，所以两个结点在根结点的不同分支上
//(2)路径不经过根结点，所以两个结点应该是次根结点中相聚最远的两个结点。 (递归思想)   
//递归本质上还是采用了后续遍历的方法。由于是从叶子结点开始的所以每次处理都是第一种情况。

//        方法二：非递归法

//采用后序遍历二叉树的同时对二叉树的结点进行更新，每次更新都要更新最大距离。

//
//*************************************


//
//定义结点结构
//
struct NODE
{
    NODE* pLeft;
    NODE* pRight;
    int nMaxLeft;
    int nMaxRight;
    char nValue;    
};
int tMaxLength=0;    //最大距离

stack<NODE*> s;

//
//求最大距离(方法一)
//
void findMaxLength1(NODE* root)
{
    //递归结束
    if(root==NULL)    return;




    //
    //左树为空
    //
    if(root->pLeft==NULL)
        root->nMaxLeft=0;

    //
    //右树为空
    //
    if(root->pRight==NULL)
        root->pRight=0;

    //
    //左树不为空
    //
    if(root->pLeft!=NULL)
    {
        findMaxLength1(root->pLeft);
    }

    //
    //右树不为空
    //
    if(root->pRight!=NULL)
    {
        findMaxLength1(root->pRight);
    }

    //
    //求左子树最大距离
    //
    if(root->pLeft!=NULL)
    {
        int nTempMax=0;
        if(root->pLeft->nMaxLeft>root->pLeft->nMaxRight)
            nTempMax=root->pLeft->nMaxLeft;
        else
            nTempMax=root->pLeft->nMaxRight;
        root->nMaxLeft=nTempMax+1;
    }

    //
    //求右子树最大距离
    //
    if(root->pRight!=NULL)
    {
        int nTempMax=0;
        if(root->pRight->nMaxLeft>root->pRight->nMaxRight)
            nTempMax=root->pRight->nMaxLeft;
        else
            nTempMax=root->pRight->nMaxRight;
        root->nMaxRight=nTempMax+1;
    }

    //
    //更新最大距离
    //
    if((root->nMaxLeft+root->nMaxRight)>tMaxLength)
        tMaxLength=root->nMaxLeft+root->nMaxRight;
}

//
//求最大距离(方法二)
//
void findMaxLength2(NODE* root)
{
    NODE *p=root;    
    NODE *have_visited=NULL; //记录上次访问的结点，主要是用在：判定根结点是       //否能访问。如果根结点的右孩子是刚访问的，那么就能访问根结点了。

    while(p!=NULL||!s.empty())
    {
        //
        //把最左分支压入栈，类似于中序遍历
        //

        while(p!=NULL)
        {
            s.push(p);
            p=p->pLeft;        
        }
        p=s.top();            

        //
        //如果右子树是空，那么后序遍历就是中序遍历
        //如果如果上次访问的是右结点，那么可以访问根结点
        //

        if(p->pRight==NULL||have_visited==p->pRight)
        {            
            //
            //以下是求最大距离的代码，不属于后序遍历
            //

            if(p->pLeft!=NULL)
            {
                p->nMaxLeft=p->pLeft->nMaxLeft+1;
                if(p->pLeft->nMaxRight+1>p->nMaxLeft)
                    p->nMaxLeft=p->pLeft->nMaxRight+1;
            }
            if(p->pRight!=NULL)
            {
                p->nMaxRight=p->pRight->nMaxRight+1;
                if(p->pRight->nMaxLeft+1>p->nMaxRight)
                    p->nMaxRight=p->pRight->nMaxLeft+1;
            }
            if((root->nMaxLeft+root->nMaxRight)>tMaxLength)
                tMaxLength=root->nMaxLeft+root->nMaxRight;
            //*************************************结束

            s.pop();
            have_visited=p;
            p=NULL;
        }
        else
        {
            p=p->pRight; //指向右子树，为下次循环，压栈做准备。

        }
    }    
}

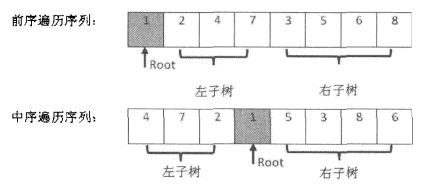
（12） 中序、先序遍历重建二叉树

二叉树的遍历方式：前序、中序和后序。每种遍历均有递归和循环两种不同方法。递归实现要比循环简洁。

//main.cpp
#include "BinaryTreeNode.h"
#include "BinaryTreeOperation.h"
#include <iostream>
#include <exception>
using namespace std;

BinaryTreeNode *ConstructCore(
	int *startPreorder,
	int *endPreorder,
	int *strartInorder,
	int *endInorder
	)
{
<span style="color:#ff0000;">	//前序遍历序列的第一个元素是根节点的值.
	int rootValue = startPreorder[0];
	BinaryTreeNode *root = new BinaryTreeNode();
	root->nValue = rootValue;
	root->pLeftChild = root->pRightChild = NULL;
</span>
	if (startPreorder == endPreorder)
	{
		if(strartInorder == endInorder && *startPreorder == *strartInorder)
			return root;
		else throw exception("Invalid input!");
	}

<span style="color:#ff9900;">	//在中序遍历中找到根节点的值.
	int *rootInorder = strartInorder;
	while(rootInorder <= endInorder && *rootInorder != rootValue)
		++rootInorder;</span>

	if(rootInorder == endInorder && *rootInorder != rootValue)
		throw exception("Invalid input.");

<span style="color:#ff0000;">	int leftLength = rootInorder - strartInorder;
	int *leftPreorderEnd = startPreorder + leftLength;</span>
	//若左子树长度大于零，则存在左子树，构建左子树
<span style="color:#ff9900;">	if (leftLength > 0)
		root->pLeftChild = ConstructCore(startPreorder + 1,leftPreorderEnd,
		strartInorder,rootInorder - 1);
	//若左子树长度小于总长度，则存在右子树，构建右子树
	if(leftLength < endPreorder - startPreorder)
		root->pRightChild = ConstructCore(leftPreorderEnd + 1,endPreorder,
		rootInorder+1,endInorder);</span>

	return root;
}


BinaryTreeNode *Construct(
	int *preorder,
	int *inorder,
	int length
	)
{
	if(preorder == NULL ||inorder == NULL || length <= 0)
		return NULL;
	return ConstructCore(preorder,preorder + length -1,
		inorder,inorder + length - 1);
}


//=========================测试代码===========================
void Test(
	char *testName,
	int *preorder,
	int *inorder,
	int length
	)
{
	if(testName != NULL)
		cout << "begins: " << testName << endl;
	cout << "the preorder sequence is: ";
	for (int i = 0;i < length;++i)
		cout << preorder[i] << " ";
	cout << endl << "the inorder sequence is: ";
	for (int i = 0;i < length;++i)
		cout << inorder[i] << " ";
	cout << endl;

	try
	{
		BinaryTreeNode *root = Construct(preorder,inorder,length);
		PrintTree(root);
		DestroyTree(root);
	}
	catch (exception& exception)
	{
		cout << "Invalid Input.\n";
	}
	//cout << endl;
}

二叉树中和为某一值的路径

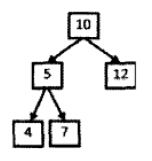
题目：输入一颗二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶结点所经过的所有的结点形成一条路径。

如下图，输入二叉树和整数22，则打印出两条路径，第一条路径包含结点10，12，第二条路径包含的结点为10，5，7.

一般的数据结构和算法的教材都没有介绍树的路径，因此对大多数应聘者而言，这是一个新概念，也就很难一下子想出完整的解题思路。这个时候我们可以试着从一两个具体的例子入手，找到规律。

以图中的二叉树为例分析，由于路径是从根节点出发到叶结点，也就是说路径是以根节点为起始点，因此i我们首先需要遍历根节点。在树的前序、中序、后序三种遍历方式中，只有前序遍历是首先访问根节点的。

按照前序遍历的顺序遍历途中的二叉树，在访问结点10之后，就会访问结点5.从二叉树结点的定义可以看出，在本题的二叉树结点中没有指向父节点的指针，访问到结点5的时候，我们是不知道前面经过了哪些结点的，除非我们把经过的路径上的结点都保存起来。每访问到一个结点的时候，我们都把当前的结点添加到路径中去。到达结点5时，路径中包含两个结点，他们的值分别是10和5.接下来遍历到结点4，我们把这个结点也添加到路径中，这个时候已经到达了叶结点，但路径上三个结点的值之和为19.这个和不等于输入的值22，因此不符合要求的路径。

我们接着要遍历其他的结点。在遍历下一个节点之前，先要从结点4回到结点5，再去遍历结点5的右子节点7.值得注意的是，回到结点5的时候，由于结点4已经不在前往结点7的路径上了，我们需要把结点4从路径中删除。接下来访问到结点7的时候，再把结点添加到路径中。此时路径中三个结点10，5，7之和刚好是22，是一条符合要求的路径。

我们最后要遍历的结点是12.在遍历这个结点之前，需要先经过结点5回到结点10.同样，每一次当从子节点回到父节点的时候，我们都需要在路径上删除子节点。最后从结点10到达结点12的时候，路径上的两个结点的值之和也是22，因此这也是一条符合条件的路径。

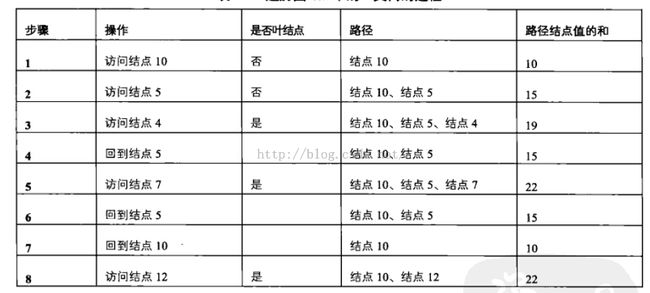
总结过程如下：

分析完前面的具体的例子之后，我们就找到了一些规律。当用前序遍历的方式访问到某一节点时，我们把该结点添加到路径上，并累加该结点的值。如果该结点为叶结点并且路径中结点值的和刚好为输入的整数，则当前的路径符合要求，我们把它打印出来。如果当前的结点不是叶结点，则继续访问它的子节点。当前结点访问结束后，递归函数将自动回到它的父节点。因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值，以确保返回父节点时路径刚好是从根节点到父节点的路径。我们不难看出保存路径的数据结构实际上是一个栈，因此路径要与递归调用状态一致，而递归调用的本质上是一个压栈和出栈的过程。

算法如下：

 #include "TreeNode.h"
 #include <vector>

 using namespace std;

 void find_path(TreeNode *pRoot, vector<int>& path, int currentSum, int elem);

 void FindPath(TreeNode *pRoot,int elem)
 {
     if(NULL == pRoot)
         return;

     vector<int> path;       /**这里不应将头结点入队*/
     int currentSum = 0;     /*路径结点数据和*/

     find_path(pRoot, path, currentSum, elem);
 }

 void find_path(TreeNode *pRoot, vector<int>& path, int currentSum, int elem)
 {
     /** 这里确实多余，因为在传递进来之前会检查这个指针是否为空
     if(NULL == pRoot)
         return;
     */

     /**一、刚加入一个节点，因此路径元素和加上这个值*/
     currentSum += pRoot->m_pValue;
     path.push_back(pRoot->m_pValue);

     /**二、如果是叶结点，并且路径结点元素的和等于elem，那么打印这条路径*/
     if(currentSum == elem && pRoot->lchild == NULL && pRoot->rchild == NULL)
     {
         cout << "A path is found: ";
         for(vector<int>::size_type i = 0; i < path.size(); i++)
             cout << path[i] << ' ';
         cout << endl;
     }

     /**三、如果左右孩子不为空*/
     if(pRoot->lchild)
         find_path(pRoot->lchild, path, currentSum, elem);
     if(pRoot->rchild)
         find_path(pRoot->rchild, path, currentSum, elem);

     path.pop_back();   /**四、返回上一个结点之前，这条路径上的尾结点需要删除*/
 }

 void test1()
 {
     TreeNode *p1 = create_Treenode(10);
     TreeNode *p2 = create_Treenode(5);
     TreeNode *p3 = create_Treenode(12);
     TreeNode *p4 = create_Treenode(4);
     TreeNode *p5 = create_Treenode(7);

     connect_Treenode(p1,p2,p3);
     connect_Treenode(p2,p4,p5);

     FindPath(p1,22);
 }

 int main()
 {
     test1();
     return 0;
 }