（1.2.6.3）最小生成树--Kruskal算法：O(elog2e) 适合稀疏图

Kruskal算法

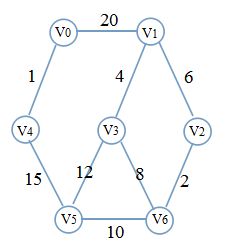
    求解最小生成树的另一种常见算法是Kruskal算法，它比Prim算法更直观。从直观上看，Kruskal算法的做法是：每次都从剩余边中选取权值最小的，当然，这条边不能使已有的边产生回路，即连接两个联通分量。

手动求解会发现Kruskal算法异常简单，下面是一个例子

先对边的权值排个序：1(0,1) 2(2,6) 4(1,3) 6(1,2) 8(3,6) 10(5,6) 12(3,5) 15(4,5) 20(0,1)

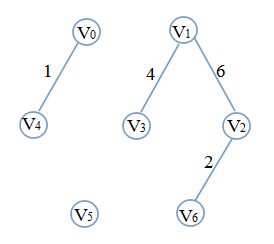
首选边1(0,1)、2(2,6)、4(1,3)、6(1,2)，此时的图是这样

显然，若选取边8(3,6)会出现环，则必须抛弃8(3,6)，选择下一条10(5,6)没有问题，此时图变成这样

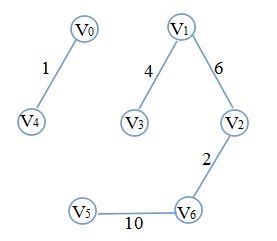
显然，12(3,5)同样不可取，选取15(4,5)，边数已达到要求，算法结束。最终的图是这样的

算法逻辑人很容易理解，但用代码判断当前边是否会引起环的出现，则很棘手。

算法说明

    为了判断环的出现，我们换个角度来理解Kruskal算法的做法：初始时，把图中的n个顶点看成是独立的n个连通分量，从树的角度看，也是n个根节点。我们选边的标准是这样的：若边上的两个顶点从属于两个不同的连通分量，则此边可取，否则考察下一条权值最小的边。

    于是问题又来了，如何判断两个顶点是否属于同一个连通分量呢？这个可以参照并查集的做法解决。它的思路是：如果两个顶点的根节点是一样的，则显然是属于同一个连通分量。这也同样暗示着：在加入新边时，要更新父节点。具体细节看代码：

 void Kruskal(MGraph G)//克鲁斯卡尔算法
 {
     int set[10], i, j;
     int k=0, a=0, b=0, min=G.arcs[a][b];

     for(i=0; i<G.vexnum; i++)
         set[i]=i;//初态，各顶点分别属于各个集合

     cout<<"最小生成树的各条边为："<<endl;

     while(k < G.vexnum-1)//最小生成树的边数等于顶点数-1
     {
         for(i=0; i<G.vexnum; i++)//寻找最小权值的边，无向网，只在上三角形中查找
             for(j=i+1; j<G.vexnum; j++)
                 if(G.arcs[i][j] < min)
                 {
                     min=G.arcs[i][j];//最小权值
                     a=i;//边的一个顶点
                     b=j;//边的另一个顶点
                 }

         min=G.arcs[a][b]=1000;//避免下次查找

         if(set[a]!=set[b])//边的两个顶点不属于同一集合
         {
             cout<<G.vexs[a]<<"-"<<G.vexs[b]<<endl;
             k++;//边数加1
             for(i=0; i<G.vexnum; i++)
                 if(set[i]==set[b])//将顶点b所在集合并入顶点a集合
                     set[i]=set[a];
         }
     }
 }