平面几何相关 由调和四边形引出的一点点调和性质
先声明这篇文章和ACM本身并没有多大关系= =
考虑上图这样一个基本构形,其中AB,AC是圆O的切线,A,P,Q三点共线,
利用相似容易证明PB/QB=PC/QC,称这样的四边形PBQC为“调和四边形”,
连接BC交APQ于D,得到下图,
那么有
AP/DP=(AC*sin∠ACP)/(DC*sin∠DCP),
AQ/DQ=(AC*sin∠ACQ)/(DC*sin∠DCQ),
注意到
sin∠ACP/sin∠DCP=sin∠CQP/sin∠BCP=PC/PB,
sin∠ACQ/sin∠DCQ=sin∠CBQ/sin∠BCQ=QC/QB,
由先前得到的结论可知PC/PB=QC/QB,
于是AP/DP=AQ/DQ,称这样的点列A,P,D,Q为“调和点列”,
调和点列是个神奇的东西= =
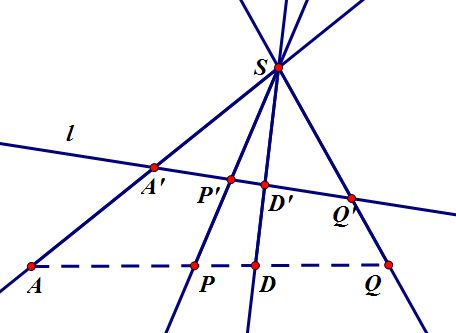
对于调和点列A,P,D,Q和直线AD外任意一点S,
称直线束SA,SP,SD,SQ为“调和线束”,
一个经典结论是,
如果SA,SP,SD,SQ为调和线束,
则任意一条直线l截这个线束得到的四个点A',P',D',Q'为调和点列,
证明只需用到正弦定理,比较简单,故此处略(liu)去(keng),
这个结论充分体现了调和点列于调和线束的对偶关系,
另一个关于调和点列的经典结论是,
对于调和点列A,P,D,Q和直线AD外任意一点S,
如果SA⊥SD,那么SD是∠PSQ的内角平分线,SA是外角平分线,
证明仍然只需用到正弦定理,比较简单,故此(ji)处(xu)略(liu)去(keng),
同时可以发现,使得SP/SQ是不为1的定值的曲线是以AD为直径的一个圆,
称这个圆为“阿波罗尼斯(Apollonius)圆”,
那么ACM大概能用到的调和性质暂时就这么多了,以后遇到就再说吧……