一：排序(1) 初级排序

—-插入排序之直接插入排序—-

基本思想：每步将一个待排序的纪录，按其关键码值的大小插入前面已经排序的文件中的适当位置上，使得插入后依然有序，直到全部插入完为止。

直接插入排序的Python实现如下：

#python3.3
#T = O(n^2)
def InsertionSort(A):
    for i in range(1,len(A)):
        key = A[i]
        j = i-1
        while j>=0 and A[j]>key:
            A[j+1] = A[j]
            j -= 1
        A[j+1] = key

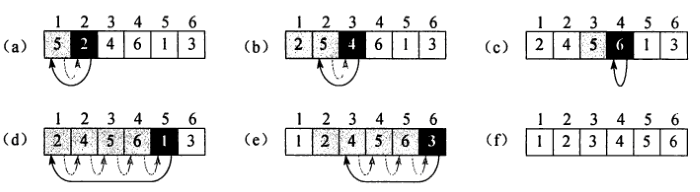
为了便于理解，图示说明执行过程。

这里引用算法导论里的插图，上图清楚的展示了插入排序的过程。这里需要注意的是，上图数组下标从1开始，而代码里遵从语言设计，数组下标从0开始。如果觉得上图的这个过程还不够形象深刻，推荐大家一个直观学习算法和数据结构的网站：http://zh.visualgo.net

评价：插入排序是稳定的、原址的，待排序记录少的时候性能不错，原始数组基本有序的情况下渐进时间复杂度为O(n)，平均情况（原始数组随机排列）和最坏情况（逆序）下，渐进时间复杂度为O(n^2)

改进与拓展：二分插入排序（减少比较次数）、链表插入排序（减少移动次数）、希尔排序（缩小增量排序）

这里要简单说说希尔排序，希尔排序是直接插入排序的改进。一方面，当数组基本有序时直接插入时间复杂度可就提高至O(n)。另一方面，直接插入排序算法简单，待排序记录少时效率也比较高。希尔排序是利用以上两点对其改进的算法。它的基本思想是：先将整个排序记录分割成若干子序列（如何分割？按照某个‘增量’间隔的记录组成一个子序列，每排完一趟，减少‘增量’，直到‘增量’为1）分别进行直接插入排序，待整个数组基本有序时，再对全体记录进行一次直接插入排序。

下面是希尔排序过程图：

图中相同颜色的记录构成一个子序列，这里的增量取5,3,1。

希尔排序的Python代码实现如下：

#python3.3
#T = O(n(lgn)^2) 根据不同的增量序列有不同
def ShellSort(A):
    increment = len(A)>>1 #增量以一半的速率减少
    while increment :
        for i in range(increment):
            for j in range(i,len(A),increment):
                key = A[j]
                k = j-increment
                while k>=i and A[k]>key:
                    A[k+increment] = A[k]
                    k -= increment
                A[k+increment] = key
        increment >>= 1

实际中，增量序列可有多种取法，如塞克威奇的《算法第四版》用了…40,13,4,1。其他有取…9,5,3,2,1 等等。具体效果如何，不如大家在实际测试后再选择。

—-选择排序之简单选择排序—-

基本思想：从所有待排序列中找到最小的元素，然后与第一个位置的元素交换。之后再从剩余元素中找到最小元素，与第二个位置的元素交换……以此类推直到整个序列有序。

简单选择排序的Python实现如下：

#python3.3
#T = O(n^2)
#从数组A的第first到第last个元素中找到最小元素，并返回对应的下标
def FindMin(A,first,last):
    minElemPos = first
    for i in range(first+1,last+1):
        if A[i] < A[minElemPos]:
            minElemPos = i
    return minElemPos   

def SelectionSort(A):
    for i in range(len(A)-1):
        minElemPos = FindMin(A,i,len(A)-1)
        A[i],A[minElemPos] = A[minElemPos],A[i] #交换两值

执行的过程可以描述如下：

评价：简单选择排序是原址的、不稳定的，任何情况下算法的渐进时间复杂度都是O(n^2)

改进与拓展：树形选择排序、堆排序

—-交换排序之冒泡排序—-

基本思想：依次比较相邻的两个数，将小数放在前面，大数放在后面。比如第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。

冒泡算法的Python实现（这里用冒泡的上浮法实现，与冒泡的下沉法原理是一样的，只不过遍历数组方向不一样）：

#python3.3
#T = O(n^2)
def BubbleSort(A):
    for i in range(len(A)-1):
        for j in range(len(A)-1,i,-1):
            if A[j] < A[j-1]:
                A[j],A[j-1] = A[j-1],A[j]

基本过程可以描述如下：

评价：冒泡排序是稳定的、原址的，基本思想和实现简单，渐进时间复杂度为O(n^2)

改进和拓展：快速排序

最后来验证下上述几个实现。

#python3.3
#测试排序算法的包装函数
def SortFuncTest(func, *args):
    print(func.__name__)
    print('Before Sort: ',end='')
    for i in args[0]:
        print("%3d"%i,end=' ')
    print('',end='\n')
    func(*args)
    print('After Sort: ',end='')
    for i in args[0]:
        print("%3d"%i,end=' ')
    print('',end='\n\n')
#测试函数
def SortTest():
    A = [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]
    SortFuncTest(InsertionSort,A[:])
    SortFuncTest(BubbleSort,A[:])
    SortFuncTest(SelectionSort,A[:])
    SortFuncTest(ShellSort,A[:])

SortTest()

运行python3.3 结果如下：
InsertionSort
Before Sort: 13 -3 -25 20 -3 -16 -23 18 20 -7 12 -5 -22 15 -4 7
After Sort: -25 -23 -22 -16 -7 -5 -4 -3 -3 7 12 13 15 18 20 20

BubbleSort
Before Sort: 13 -3 -25 20 -3 -16 -23 18 20 -7 12 -5 -22 15 -4 7
After Sort: -25 -23 -22 -16 -7 -5 -4 -3 -3 7 12 13 15 18 20 20

SelectionSort
Before Sort: 13 -3 -25 20 -3 -16 -23 18 20 -7 12 -5 -22 15 -4 7
After Sort: -25 -23 -22 -16 -7 -5 -4 -3 -3 7 12 13 15 18 20 20

ShellSort
Before Sort: 13 -3 -25 20 -3 -16 -23 18 20 -7 12 -5 -22 15 -4 7
After Sort: -25 -23 -22 -16 -7 -5 -4 -3 -3 7 12 13 15 18 20 20

参考：算法导论，算法4（塞克威奇），谷歌、百度