GEEK学习笔记— —程序员面试宝典笔记(五)
所谓笔记,就是比较个人的东西,把个人觉得有点意思的东西记录下来~~
程序员面试宝典笔记(一)基本概念
程序员面试宝典笔记(二)预处理、const和sizeof
程序员面试宝典笔记(三)auto_ptr、递归
程序员面试宝典笔记(四)面向对象、类型转换、static
程序员面试宝典笔记(五)数据结构基础
程序员面试宝典笔记(六)软件测试
题目
请讲述heap与stack的差别。
答案
栈区(stack):由编译器自动分配和释放,存放函数的参数值、局部变量的值等。其操作方式类似于数据结构中的栈。
堆区(heap):一般由程序员分配和释放,若程序员不释放,程序节束时可能由操作系统回收。注意它与数据结构中的堆是两回事,分配方式倒是类似于链表。
1.申请方式
栈:由系统自动分配。
堆:需要程序员自己申请,并指明大小。
2.申请后系统的响应
栈:只要栈的剩余空间大于所申请空间,系统将为程序提供内存,否则将报异常提示栈溢出。
堆:操作系统有一个记录空闲内存地址的链表,当系统收到程序的申请时,会遍历该链表,寻找第一个空间大于所申请空间的堆节点,然后将该节点从空闲节点链表中删除,并将该节点的空间分配给程序。对于大多数系统,会在这块内存空间中的首地址处记录本次分配的大小,这样,代码中的delete语句才能正确地释放本内存空间。另外,由于找到的堆节点的大小不一定正好等于申请的大小,系统会自动地将多余的那部分重新放入空闲链表中。
3.申请大小的限制
栈:在Windows下,栈是向低地址扩展的数据结构,是一块连续的内存的区域。这句话的意思是栈顶的地址和栈的最大容量是系统预先规定好的,在Windows下,栈的大小是2MB(也有的说是1MB,总之是一个编译时就确定的常数),如果申请的空间超过栈的剩余空间,将提示overflow。因此,能从栈获得的空间较小。
堆:堆是向高地址扩展的数据结构,是不连续的内存区域。这是由于系统是用链表存储空闲内存地址的,自然是不连续的。而链表的遍历方向是由低地址向高地址,堆的大小受限于计算机系统中有效的虚拟内存。由此可见,堆获得的空间比较灵活,也比较大。
4.申请效率的比较
栈:由系统自动分配,速度较快。但程序员无法控制。
堆:是由new分配的内存,一般速度比较慢,而且容易产生内存碎片,不过用起来最方便。
5.堆和栈中的存储内容
栈:在函数调用时,第一个进栈的是主函数中的下一条指令(函数调用语句的下一条可执行语句)的地址,然后是函数的各个参数。在大多数的C编译器中,参数是由右往左入栈的,然后是函数中的局部变量。注意静态变量是不入栈的。当本次函数调用节束后,局部变量先出栈,然后是参数,最后栈顶指针指向最开始存的地址,也就是主函数中的下一条指令,程序由该点继续运行。
堆:一般是在堆的头部用一个字节存放堆的大小。堆中的具体内容由程序员安排。
题目
前序遍历二叉树值为abcdefg,下面哪个不可能是中序遍历。
A.abcdefg
B.gfedcba
C.bcdefga
D.bceadfg
解析
二叉树遍历原则如下:前序遍历是根左右,中序遍历是左根右,后序遍历是左右根。如果前序遍历二叉树值为abcdefg,那么a一定是根,这样我们再来看选项D,如果bceadfg是中序遍历,那么bce在左,a为根,dfg在右。根据前序遍历,bce就一定在dfg左边,所以前序遍历二叉树值不可能为abcdefg。
答案
D
题目
有一个二叉搜索树用来存储字符’A’, ‘B’, ‘C’,’D’,’E’,’F’,’G’,’H’。下面哪个结果是后序树遍历结果
A.ADBCEGFH
B.BCAGEHFD
C.BCAEFDHG
D.BDACEFHG
解析
二叉搜索树(Binary Search Tree),或者是一棵空树,或者是具有下列性质的二叉树:对于树中的每个节点X,它的左子树中所有关键字的值都小于X的关键字值,而它的右子树中的所有关键字值都大于X的关键字值。这意味着该树所有的元素都可以用某种统一的方式排序。
二叉搜索树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉搜索树的存储节构。中序遍历二叉搜索树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉搜索树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。每次插入的新的节点都是二叉搜索树上新的叶子节点,在进行插入操作时,不必移动其他节点,只需改动某个节点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,即O(log(n))。
二叉树的一个重要的应用是它们在查找中的使用。二叉搜索树的概念相当容易理解,二叉搜索树的性质决定了它在搜索方面有着非常出色的表现:要找到一棵树的最小节点,只需要从根节点开始,只要有左儿子就向左进行,终止节点就是最小的节点。找最大的节点则是往右进行。
拿A选项举例说明
ADBCEGFH
->(H) 左子树(ADBCEGF),右子树(空) (左子树必须都小于根H,右子树都大于根H)
–>(F)左子树(ADBCE),右子树(G)
—>(E)左子树(ADBC),右子树(空)
—->(C)剩下(ADB)不能区别左子树,右子树,所以选项A不成立;
答案
C
题目
下面哪个序列不是下图的一个拓扑排序?
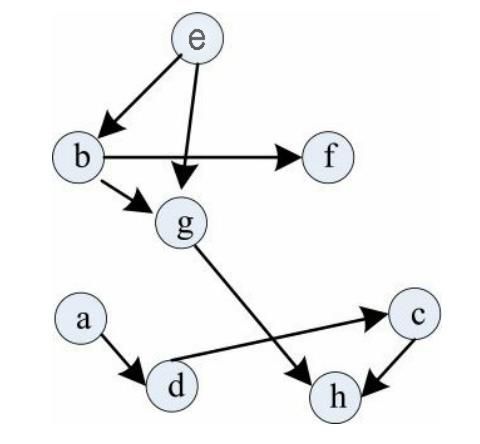
A.ebfgadch
B.aebdgfch
C.adchebfg
D.aedbfgch
解析
有向图拓朴排序算法的基本步骤如下:
1>从图中选择一个入度为0的顶点,输出该顶点;
2>从图中删除该顶点及其相关联的弧,调整被删弧的弧头结点的入度(入度-1);
3>重复执行1、2直到所有顶点均被输出。
选项C内容adch执行到h时候,h入度不为0,所以错误。
答案
C
题目
下面是邻接表,以[0]点出发,求深度优先遍历和广度优先遍历结果。
[0] -> [1] -> [5] -> [6] -> END
[1] -> [0] -> [2] -> END
[2] -> [1] -> [3] -> END
[3] -> [2] -> [4] -> [7] -> END
[4] -> [3] -> [5] -> [8] -> END
[5] -> [4] -> [0] -> END
[6] -> [0] -> [8] -> [7] -> END
[7] -> [6] -> [8] -> [3] -> END
[8] -> [6] -> [7] -> [4] -> END解析
深度优先遍历(DFS),一般用栈实现。
1>首先访问出发点v,并将其标记为已访问过;然后依次从v出发搜索v的每个邻接点w。
2>若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。
3>若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过
程,直至图中所有顶点均已被访问为止。
1、先访问0的第一个邻接点1
2、访问1的第一个邻接点0,0已被访问,访问第二个邻接点2
3、访问2的第一个邻接点1,1已被访问,访问第二个邻接点3
4、访问3的第一个邻接点2,2已被访问,访问第二个邻接点4
5、访问4的第一个邻接点3,3已被访问,访问第二个邻接点5
6、访问5的第一个邻接点4,4已被访问,访问第二个邻接点0,0已被访问,5的邻接点都已被访问
7、返回访问4的第三个邻接点为8
8、访问8的第一个邻接点6
9、访问6的第一个邻接点0,0已被访问,访问第二个邻接点8,8已被访问,访问第三个邻接点7。
所有节点都被访问过,最后是END。按照顺序就是0 1 2 3 4 5 8 6 7 END
广度优先遍历(BFS),一般用队列实现。
1>从图中某个顶点V0出发,并访问此顶点。
2>从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点。
3>重复步骤2,直到全部顶点都被访问为止。
1、先访问0的邻接点1 5 6
2、访问1的未访问过的邻接点2
3、访问5的未访问过的邻接点4
4、访问6的未访问过的邻接点8 7
5、访问2的未访问过的邻接点3
所有节点都被访问过,最后是END。按照顺序就是0 1 5 6 2 4 8 7 3 END
答案
深度优先遍历 0 1 2 3 4 5 8 6 7 END
广度优先遍历 0 1 5 6 2 4 8 7 3 END
题目
在百度或淘宝搜索时,每输入字符都会出现搜索建议,比如输入“北京”,搜索框下面会以北京为前缀,展示“北京爱情故事”、“北京公交”、“北京医院”等等搜索词。实现这类技术后台所采用的数据结构是什么?
答案
Trie树,又称单词查找树、字典树,是一种树形结构,是一种哈希树的变种,是一种用于快速检索的多叉树结构。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。Trie树的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
对于搜索引擎,一般会保留一个单词查找树的前N个字(全球或最近热门使用的);对于每个用户,保持Trie树最近前N个字为该用户使用的结果。
如果用户点击任何搜索结果,Trie树可以非常迅速并异步获取完整的部分/模糊查找,然后预取数据,再用一个Web应用程序可以发送一个较小的一组结果的浏览器。
题目
用二进制来编码字符串“abcdabaa”,需要能够根据编码,解码回原来的字符串,最少需要多长的二进制字符串?
解析
哈夫曼编码问题:字符串“abcdabaa”有4个a、2个b、1个c、1个d。构造哈夫曼树,a编码0(1位),b编码10(2位),c编码110(3位),d编码111(3位)。这个字符串的总长度为:1*4+2*2+3*1+3*1=14。
答案
B