Huffman编码
1.从树中一个结点到另外一个结点之间分支构成两个结点之间的路径,是、路径上的分支数目叫做路径长度
2.树的路径长度就是从树根到每一个结点的路径长度之和
3.带权路径长度WPL最小的二叉树称作赫夫曼树
4.若要设计长短不等的编码,则必须是任一字符的编码的前缀,这种编码称为前缀编码
5.一般地,设需要编码的字符集为{d1,d2,...,dn},各个字符在电文中出现的次数或频率集合为{w1,w2,...,wn},以d1,d2,...,dn作为叶子结点,以w1,w2,...,wn作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,这就是赫夫曼编码
举个例子:
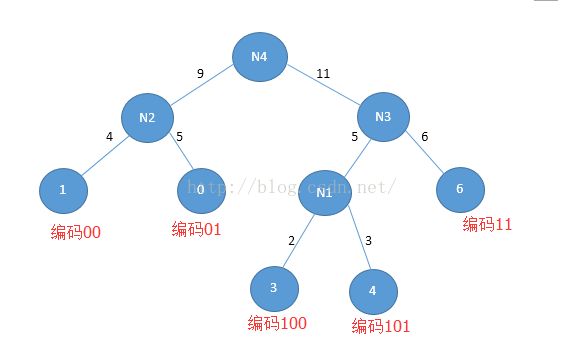
0,1,2,3,4出现的频率分别为5,4,6,2,3
1先把有权值的叶子结点按照从小到大的顺序排成一个有序序列,3 2, 4,3, 1 4, 1 5, 2 6
2.取两个权值最小的作为一个新结点N1,较小的是左孩子,新的孩子的权值是2+3=5,然后再放进队列1 4,1 5,N1 5, 2 6
3.同样二的步骤,知道序列里面只有一个结点
WPL=5*2+4*2+2*3+3*3+6*2=45
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
typedef struct HTNode{
char c;
int freq;
HTNode *lchild, *rchild;
HTNode(char key='\0', unsigned int fr=0, HTNode *l=NULL, HTNode *r=NULL):
c(key),freq(fr),lchild(l),rchild(r){};
}HTNode,*pNode;
//重载优先队列里的比较运算符
struct cmp{
bool operator()(pNode node1, pNode node2){
return node1->freq>node2->freq;
}
};
priority_queue<pNode,vector<pNode>,cmp> pq;
//建Huffman Tree
void HuffmanTree(int n){
pNode left,right;
//从优先队列中找出优先级最小的两个元素,合并,并
//把它加入到优先队列中
while(pq.size()>1){
pNode tmp=new HTNode;
left=pq.top();
pq.pop();
right=pq.top();
pq.pop();
tmp->lchild=left;
tmp->rchild=right;
tmp->freq=left->freq+right->freq;
pq.push(tmp);
}
}
//中序遍历
int B=0;
void PrintCode(pNode t, string str){
if(t==NULL)
return;
//左子树
if(t->lchild){
str+='0';
PrintCode(t->lchild,str);
}
//叶子结点
if(t->lchild==NULL && t->rchild==NULL){
B+=t->freq*str.length();
}
str.erase(str.end()-1); //删除最后一个字符
//右子树
if(t->rchild){
str+='1';
PrintCode(t->rchild,str);
}
}
int main(){
int n;
cin>>n;
char c;
int freq;
string str="";
for(int i=0;i<n;i++){
cin>>c>>freq;
pNode p=new HTNode;
p->c=c;
p->freq=freq;
pq.push(p);
}
HuffmanTree(n);
PrintCode(pq.top(), str);
cout << B << endl;
return 0;
}