组合优化问题求解方法GA-交叉算子的总结

组合优化问题求解方法GA-交叉算子的总结

离散的组合优化问题：通过数学方法的研究去寻找离散事件的最优编排分组、次序或者筛选等。这些问题的描述都非常简单，并且具有很强的工程性，但最优化的求解很困难。

 

组合优化问题具有一个共同的特点，就是爆炸式增长的候选集(组合爆炸)，例如对于旅行商问题而言，其候选集的数量为(N-1)!,其中N为城市的数目。对于这种NP-hard问题，如果采用穷举遍历，那么消耗的时间是指数级增长的，因此解决大规模的TSP采用穷举遍历是不现实的。

 

为了解决组合优化的问题，通常有两大类算法。一类是确定性的算法：比如穷举算法，这类算法由于消耗时间过长以及极大的存储空间要求，已经被现有的性能较优的启发式算法替代。

 

第二类是近似算法，这类算法通常能找到足够好的近似解，不保证能找到最优解。包括：模拟退火算法、遗传算法、粒子群算法、蚁群算法、禁忌搜索算法等。

近年来，很多学者对这些启发式算法做了大量的改进，有些提出了两种算法的混合算法，使得其性能得到很大的提高。有大量的论文和实验证明遗传算法的拥有较有的求解性能。这里先对遗传算法做一些总结。

 

遗传算法的性能由初始解的产生、杂交算法和变异算子决定。其中杂交算子和变异算子起着决定性的作用。

 

1999年，P. LARRANAGA et.al【1】 等人对现有的杂交算子做了全面的总结和实验，他们选取了8种杂交算子(AP、CX、ER、OX1、OX2、PMX、POS、VR)和6种变异算子(DM、EM、ISM、IVM、SIM、SM)，产生了48种组合，分别使用这48种组合解决相同的TSP问题，并比较结果。得出结论：（交叉算子中，OX优于PMX，PMX优于CX【2】）杂交算子按从优到劣排列为：ER、OX1、POS、OX2；变异算子按从优到劣排列为：DM、IVM、ISM.

同时ER也是最快速的杂交算子。

但是这些算子的性能排序不是对于所有的组合优化问题都是不变的。对于具体的问题，适用于该问题的最佳算子应该是不同的。在设计杂交算子时，不同的问题需要考虑的保留的信息不同。

 

TSP问题是一类顺序排列问题，这类问题中，邻域信息有非常重要的作用，而位置信息影响不大。因此在设计杂交算子时，若考虑到保留较多的邻域信息，那么肯定有更好的性能，因此ER算子的性能比其他算子的性能都好。

 

然而在其他schedule问题的规划时，邻域信息可能并不重要，顺序反而成为了最需要考虑的因素。这时这些算子的性能排序刚好和上面相反。【3】

因此对于不同的问题，需要具体考虑不同的算子。

 

在文献【4】中，作者对近年来用于解决TSP问题的优秀的启发式算子进行了总结和性能比较，包括PMX、EPMX、GSX-2、GXs、VGX、UHX、DPX。实验结果显示GXs、UHX、DPX有更高的性能。

 

在文献【5】中，作者比较了OX、NWOX、UPMX、PMX、CX的性能，最好的是OX，最差的是CX。

 

【1】Genetic Algorithms for the Travelling Salesman Problem: A Review of Representations and Operators .   Artificial Intelligence Review 13: 129–170, 1999.

【2】Oliver, I. M., Smith, D. J. & Holland, J. R. C. (1987). A Study of Permutation Crossover Operators on the TSP. Genetic Algorithms and Their Applications.

【3】A comparision of Genetic sequencing operators. 1991

【4】Study of Some Recent Crossovers Effects on Speed and Accuracy of Genetic Algorithm, Using Symmetric Travelling Salesman Problem. 2015

【5】A Comparative Study of Adaptive Crossover Operators for Genetic Algorithms to Resolve the Traveling Salesman Problem. 2011

GA的关键步骤：

3.1 编码

    TSP问题编码一般有五种种不同的方式：

• 基于二进制的编码
• 基于矩阵的编码
• 基于邻接的编码
• 基于索引（Ordinary）的编码
• 基于路径的编码

    基于二进制的编码是一种传统的编码方式，但是这种方式的编码，在经过遗传操作以后很难保证后代还是一个可行解，还需要另外的修正操作；基于矩阵的编码、邻接的编码以及索引的编码均比较复杂，并且需要占用大量的内存，应用的不是很广泛；目前最普遍用的编码方式就是基于路径的编码方式，因为它最直观最容易理解，操作起来也比较方便。以下将主要介绍基于路径的编码方式以及相关的遗传操作。

例如：

一个TSP问题，有六个城市{1,2,3,4,5,6}，那么用基于路径的编码(1 3 5 4 6 2)就可以表示为一个个体。

3.2 交叉操作

    下面主要介绍几种常见的交叉操作的方式。

3.2.1 部分匹配法（Partially Matching Crossover， PMX）

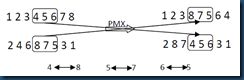
    以两个父代个体为例：（1 2 3 4 5 6 7 8）和（2 4 6 8 7 5 3 1），随机选择两个交叉的点，假如第一个点为位置4，第二个交叉点为位置6，那么在两个点之间的位置将进行交叉，其它的位置进行复制或者用相匹配的数进行替换。在此实例中，第一个父代个体中4 5 6被选中，第二个父代个体中，8 7 5被选中。那么4 与8，5与7,6与5相匹配。匹配过程和如图2所示。

图2 PMX交叉操作

    首先将4 5 6与8 7 5分别加入到子代2和子代1中相应的位置，然后将其他位置上的数字直接复制到相应的后代中，如果该数字已经在该子代中已经存在，则用相应的匹配法则进行替换，例如子代1中将7复制进去的时候，发现7已经存在在子代中，通过查找相应的匹配法则，发现，7与5匹配，然后复制5，又发现5也已经存在在该子代中，在此查找匹配法则，发现5与6匹配，将6复制，6不存在在该子代中，所以可以将6复制进去，如此反复，知道子代中城市的数目达到定义的长度，该子代创建完成。

3.2.2 循环交叉法（Cycle Crossover， CX）
    依旧以两个父代个体为例：（1 2 3 4 5 6 7 8）和（2 4 6 8 7 5 3 1），在构造子代的过程中，首先从父代1中选取第一个元素，然后查找父代2中对应位置的元素在在父代1中的位置，将这个位置对应的元素假如到子代1中，如此过程反复，直到找到一个元素对应的父代2元素等于起始元素，次循环结束，然后将剩余未填充的位置用父代2相应的位置的元素进行填充，这样就可以完成子代1的创建。子代2创建方法类似。CX操作过程如图2所示。

图3 CX操作

    首先选择父代1中的第一个元素1，将它加入到子代1中，然后检查父代2中对应位置，该位置元素为2，在父代1中查找该元素，该元素在父代1中的位置为2， 将2加入到子代1的第二个位置，再次检查父代2中第二个位置的元素，它为4，然后查找它在父代1中的位置为4，将4加入到子代1的第四个位置，然后将其加入到子代1中对应的位置4，在检查父代2中该位置的元素，它为8，查找到它在父代1中的位置为8，然后将其加入到子代1中位置8，再次查找父代2中位置8的元素，它为1，等于起始选择的元素，循环结束，然后将子代1中3,5,6,7元素为空的位置，用父代2对应位置的元素进行填充，这些元素为6,7,5,3，所以得到的子代1为（1 2 5 4 7 5 3 8）。同样的方法，得到子代2为（2 4 3 8 5 6 7 1）。

3.2.3 次序交叉法1（Order Crossover， OX1）

    还以两个相同的父代个体为例：（1 2 3 4 5 6 7 8）和（2 4 6 8 7 5 3 1），随机选择两个交叉的点，假如第一个点为位置3，第二个交叉点为位置5，那么在两个点之间的位置将进行交叉。然后从第二个交叉点开始，将原来相应的父代按照顺序进行填充，如果选择的元素已经存在在该子代中，跳过该元素，选择下一个元素，这种过程反复进行，知道所有的城市都被选择一次。在此实例中，第一个父代个体中3 4 5被选中，第二个父代个体中，6 8 7被选中。匹配过程和如图4所示。

图4 OX1操作

    首先，将选择的位串进行替换，即3 4 5换到子代2中，6 8 7换到子代1中。现在从第二个交叉点开始，将父代1中的基因插入到子代1中， 所以，1 插入到第六个位置，2 插入到第七个位置，3插入到第八个位置，第二个交叉点后面已经填充满，将剩下的插入到第一个插入点前面的位置，所以4插入到第一个位置，5插入到第二个位置。这样，子代1构建完成。同样地方法，可以构建子代2.当遇到子代中已经存在的基因，就跳到下一个。

3.2.4 次序交叉法2（Order Crossover， OX2）

    还以两个相同的父代个体为例：（1 2 3 4 5 6 7 8）和（2 4 6 8 7 5 3 1），随机选择几个交叉的点，假如第一个点为位置2，第二个交叉点为位置是3，第三个为位置6。首先找到父代2中相应位置的基因在父代1中位置，然后将其用父代2中选择的位置的基因进行替换插入到子代1中相应的位置中。然后将其它的位置用OX1相似的方法进行填充。这样就可以得到子代1.同样，替换角色，可以得到子代2。具体的操作过程如图5所示。

图5 OX2操作

    首先找到父代2中第，2,3以及第六个位置的基因，它们为4,6和5，这三个基因在父代1中的位置为4,5和6，将它们替换成4,6,5,加入到子代1中相应的位置，然后将父代1中的基因按照顺序插入到子代1中，如果该基因已经存在在位串中，则跳过该基因，继续下一个。这样就可以构建完子代1。子代2也可以以相同的方法构造完成。

3.2.5 基于位置的交叉法（Position Based Crossover， POS）

    还以两个相同的父代个体为例：（1 2 3 4 5 6 7 8）和（2 4 6 8 7 5 3 1），随机选择几个交叉的点，假如第一个点为位置2，第二个交叉点为位置是3，第三个为位置6。将两个父代中这些选择基因按照顺序交换，并且插入到子代1和2中。然后对其它位置的基因，按照顺序插入。具体操作过程如图6所示。

图6 POS操作

    首先将2 3 6和4 6 8交换，分别插入到子代2和子代1相应的位置2,4,6中，然后将将父代1和父代2中的基因按照顺序插入到子代1和2中，如果该基因已经存在在位串中，则跳过该基因，继续下一个，知道位串的长度等于定义的长度。

3.2.6 交替位置交叉法（Alternating Position Crossover，APX）

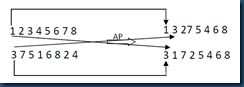
    以两个父代个体为例：（1 2 3 4 5 6 7 8）和（3 7 5 1 6 8 2 4），APX是一种简单的交叉操作方法，它是轮流选择父代1和2中的基因，直到子代的长度达到定义的长度为止。具体操作如图7所示。

图7 APX操作

    首先选择父代1中的第一个元素1，加入到子代1中，然后选择父代2中的第一个元素3，它不等于1所以也加入到子代1中，然后再选择父代1中的第二个元素2，它也不包含在当前的位串中，所以，也加入进去，然后再选择父代2中的第二个元素，……，直到子代1的长度达到8为止。同样的方法，可以得到子代2.

3.3 变异操作

    同样地，下面介绍几种常见的变异操作方法。

3.3.1 替换变异（Displacement Mutation， DM）

    DM先从父代个体中选择一个子位串，然后再随机在剩下的位串中选择一个为止，并插入该子位串，如图8所示。

图8 DM操作

3.3.2 交换变异（Exchange Mutation， EM）

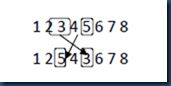
      EM是从父代个体中选择两个基因位置，然后互换这两个位置的基因。如图9所示。

图9 EM操作

3.3.3 插入变异（Insertion Mutation， IM）

    IM和DM类似，唯一的区别在于它是从父代个体中只选择一个基因，然后随机的插入到剩下的基因串中。如图10所示。

图10 IM操作

3.3.4 简单倒位变异（Simple Inversion Mutation， SIM）

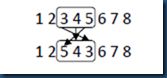
    SIM先从父代个体中选择一个基因串，然后将这个基因串中所有的基因倒位放置，如图11所示。

图11 SIM操作

3.3.5 倒位变异（Inversion Mutation， IVM）

    IVM在SIM的基础上，随机选择一个插入位置，将这个到位后的基因串在插入到其中。如图12所示。

图12 IVM操作

3.3.6 争夺变异（Scramble Mutation， SM）

    SM非常简单，先随机从父代个体中选择一个基因串，然后将除了第一个基因外的基因均向前移动一位，将第一个基因移到最后一位。具体操作过程如图13所示。

图13 SM操作