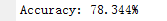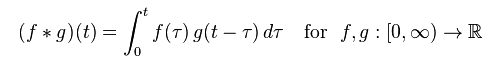卷积神经网络初探 | 数据科学家联盟 http://dataunion.org/20942.html
转载自:
卷积神经网络初探 | 数据科学家联盟
http://dataunion.org/20942.html
前言
目前为止我已经完整地学完了三个机器学习教程:包括“Stanford CS229”,”Machine Learning on Coursrea” 和 “Stanford UFLDL”,卷积神经网络是其中最抽象的概念。
维基百科对卷积的数学定义为:
由于卷积常用与信号处理,很多人基于“输入->系统->响应”这一模型来解释卷积的物理意义,这里转载一个非常通俗的版本:
比 如说你的老板命令你干活,你却到楼下打台球去了,后来被老板发现,他非常气愤,扇了你一巴掌(注意,这就是输入信号,脉冲),于是你的脸上会渐渐地鼓起来 一个包,你的脸就是一个系统,而鼓起来的包就是你的脸对巴掌的响应,好,这样就和信号系统建立起来意义对应的联系。下面还需要一些假设来保证论证的严谨: 假定你的脸是线性时不变系统,也就是说,无论什么时候老板打你一巴掌,打在你脸的同一位置,你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包,并 且假定以鼓起来的包的大小作为系统输出。好了,下面可以进入核心内容——卷积了!
如果你每天都到地下去打台球,那么老板每天 都要扇你一巴掌,不过当老板打你一巴掌后,你5分钟就消肿了,所以时间长了,你甚至就适应这种生活了……如果有一天,老板忍无可忍,以0.5秒的间隔开始 不间断的扇你的过程,这样问题就来了,第一次扇你鼓起来的包还没消肿,第二个巴掌就来了,你脸上的包就可能鼓起来两倍高,老板不断扇你,脉冲不断作用在你 脸上,效果不断叠加了,这样这些效果就可以求和了,结果就是你脸上的包的高度随时间变化的一个函数了(注意理解);如果老板再狠一点,频率越来越高,以至 于你都辨别不清时间间隔了,那么,求和就变成积分了。可以这样理解,在这个过程中的某一固定的时刻,你的脸上的包的鼓起程度和什么有关呢?和之前每次打你 都有关!但是各次的贡献是不一样的,越早打的巴掌,贡献越小,所以这就是说,某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的 输出,然后再把不同时刻的输出点放在一起,形成一个函数,这就是卷积,卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消 肿,可是如果连续打,几个小时也消不了肿了,这难道不是一种平滑过程么?反映到剑桥大学的公式上,f(a)就是第a个巴掌,g(x-a)就是第a个巴掌在 x时刻的作用程度,乘起来再叠加就ok了,大家说是不是这个道理呢?我想这个例子已经非常形象了,你对卷积有了更加具体深刻的了解了吗?
这是一些尝试解释卷积的文章:
http://www.guokr.com/post/342476/
http://blog.csdn.net/yeeman/article/details/6325693
https://zh.wikipedia.org/wiki/%E5%8D%B7%E7%A7%AF
而在图像处理中通常使用离散形式的卷积,在下一节中介绍。
卷积特征提取(convolution)
卷积特征提取的过程
假设有一个稀疏自编码器 SAE,训练使用的是 3×3 的小图。将 SAE 用作深度网络的隐藏层时,它依然只接受 3×3 的数据作为输入,且假设这个隐藏层有 k 个单元(每个单元也被称为一个卷积核 – Convolution Kernel,由对应的权值向量 W 和 b 来体现)。
每个隐藏单元的输入是用自己的权值向量 W 与 3×3 的小图做内积,再与截距项相加得到的:
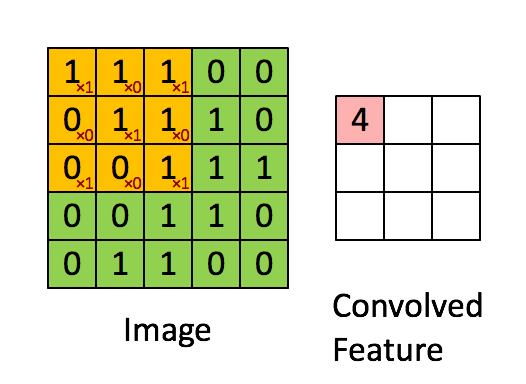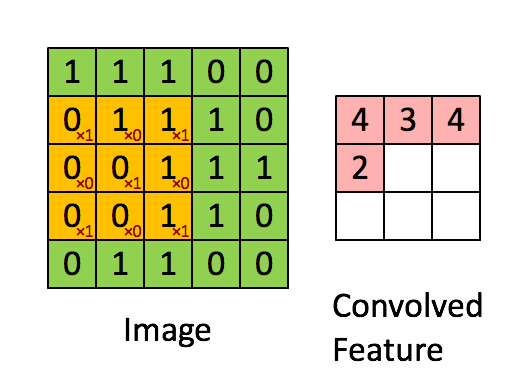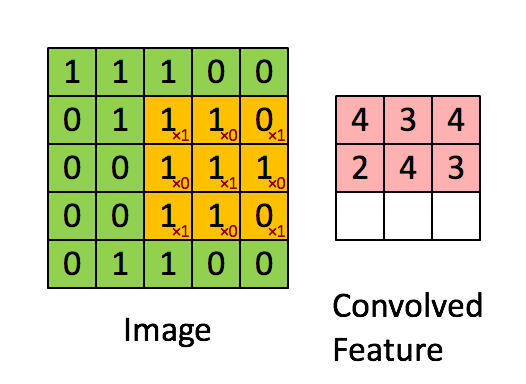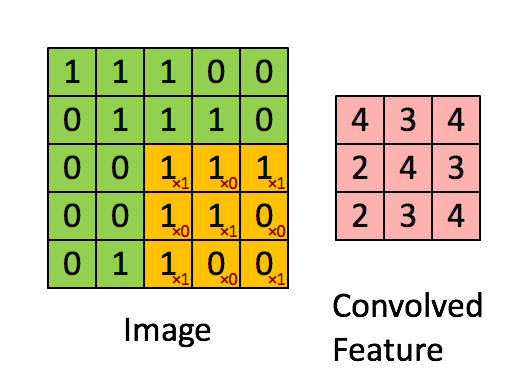
假如深度网络的输入是 5×5 的大图,SAE 要从中提取特征,必须将 5×5 的大图分解成若干 3×3 的小图并分别提取它们的特征。分解方法就是:从大图的 (1, 1)、(1, 2)、(1, 3)、… 、(3, 3)等 9 个点开始分别作为小图的左上角起点,依次截取 9 张带有重合区域的小图,然后分别提取这 9 张小图的特征:
所以,每个隐藏单元将有 9 个输入,不同于之前的 1 个。然后将所有输入分别导入激活函数计算相应的输出,卷积特征提取的工作就完成了。
对于本例,隐藏层所提取的特征共有 9×k 个;更一般化地,如果大图尺寸是 r×c,小图尺寸是 a×b,那么所提取特征的个数为:
![]()
卷积特征提取的原理
卷积特征提取利用了自然图像的统计平稳性(Stationary):
自然图像有其固有特性,也就是说,图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征。
池化(Pooling)
池化过程
在完成卷积特征提取之后,对于每一个隐藏单元,它都提取到 (r-a+1)×(c-b+1)个特征,把它看做一个矩阵,并在这个矩阵上划分出几个不重合的区域,然后在每个区域上计算该区域内特征的均值或最大值,然后用这些均值或最大值参与后续的训练,这个过程就是【池化】。
池化的优点
- 显著减少了参数数量
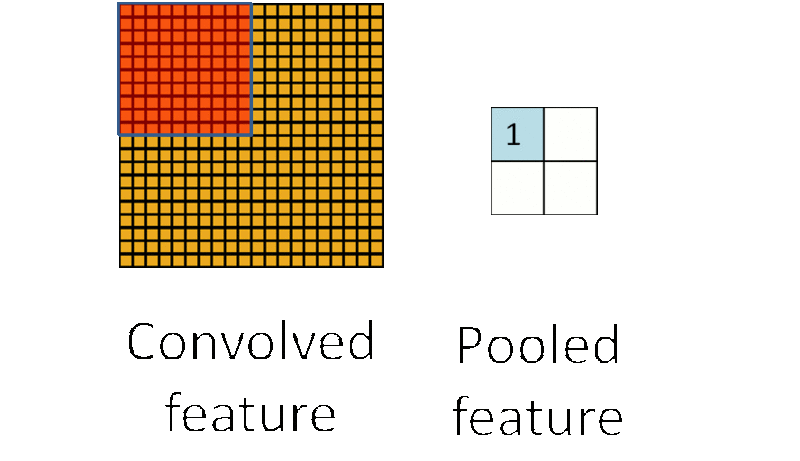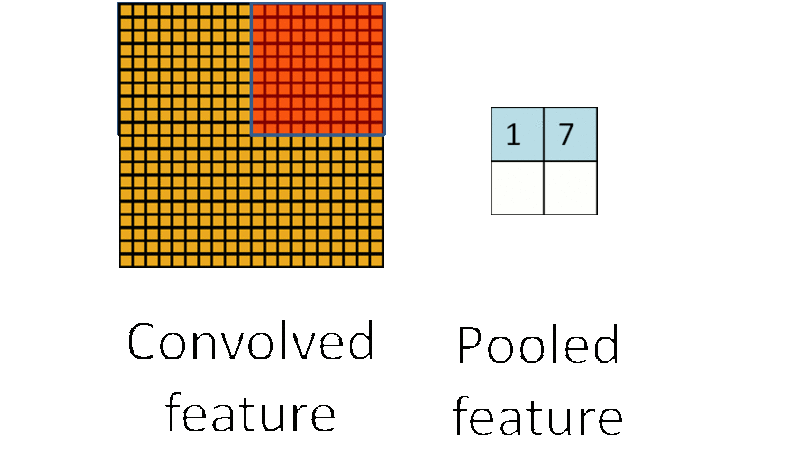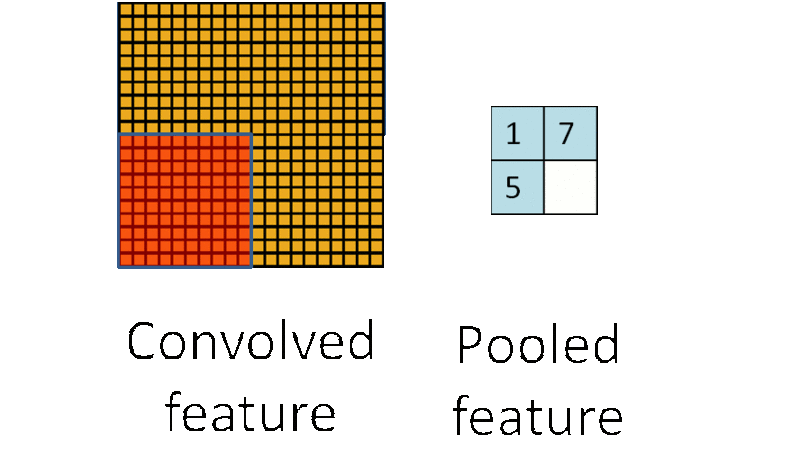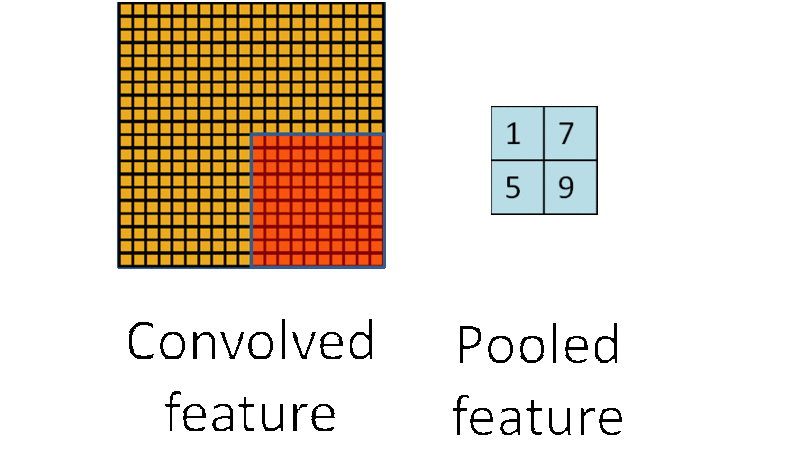
- 池化单元具有平移不变性 (translation invariant)有一个 12×12 的 feature map (隐藏层的一个单元提取到的卷积特征矩阵),池化区域的大小为 6×6,那么池化后,feature map 的维度变为 2×2。
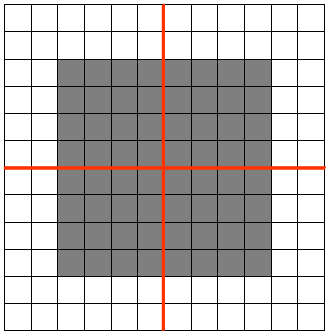
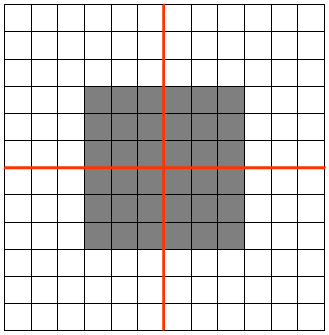
假设原 feature map 中灰色元素的值为 1,白色元素的值为 0。如果采用 max pooling,那么池化后左上角窗口的值为 1。如果将图像向右平移一个像素:
池化后左上角窗口的值还是 1。如果将图像缩小:
池化后左上角窗口的值依然是 1。
通常我们认为图像经过有限的平移、缩放、旋转,不应改变其识别结果,这就要求经过平移、缩放、旋转的图片所提取的特征与原图所提取的特征相同或相似,因此分类器才能把它们识别成同一类。
几种池化方式
比较主流的池化方式有如下几种:
- 一般池化(General Pooling): max pooling 和 average pooling现在已经知道了 max pooling 与 average pooling 的几何意义,还有一个问题需要思考:它们分别适用于那些场合?在不同的场合下,它们的表现有什么不一样?为什么不一样?
网络上有人这样区分 max pooling 和 average pooling:
“average对背景保留更好,max对纹理提取更好”。
限于篇幅以及我的理解还不深,就不展开讨论了,如果以后需要,我会深入研究一下。
- 重叠池化(Overlapping Pooling)重叠池化的相邻池化窗口之间会有重叠区域。
- 空间金字塔池化(Spatial Pyramid Pooling)空间金字塔池化拓展了卷积神经网络的实用性,使它能够以任意尺寸的图片作为输入。
- 下面列出一些研究池化的论文:http://yann.lecun.com/exdb/publis/pdf/boureau-icml-10.pdf
http://yann.lecun.com/exdb/publis/pdf/boureau-cvpr-10.pdf
http://yann.lecun.com/exdb/publis/pdf/boureau-iccv-11.pdf
http://ais.uni-bonn.de/papers/icann2010_maxpool.pdf
汇总
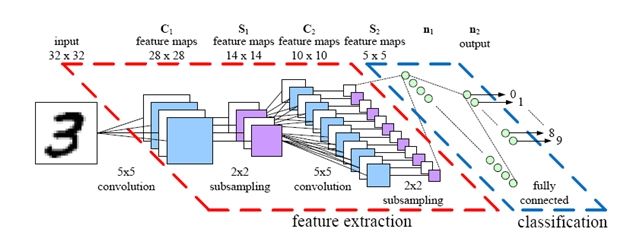
有 m 张彩色自然图片拿来训练一个神经网络,使它能够对图片中的物体做分类。训练过程可以大致分为以下几步:
- 从图片库中随机裁剪出相同尺寸的小图若干张,用来训练一个稀疏自编码器 C1;
- 以 C1 作为第一个卷积层,从原图中做卷积特征提取;
- 在 C1 下游添加一个池化层 S1,对 C1 所提取的特征做池化计算;
- 如果需要提取更加抽象的特征,在 S1 之后添加卷积层 C2,C2 是一个使用 S1 的数据进行训练的稀疏自编码器;
- 在 C2 下游添加一个池化层 S2,如果需要提取进一步抽象的特征,重复添加卷积层与池化层即可;
- 以最后一个池化层的输出作为数据训练分类器。
课后作业(Convolution and Pooling)
In this exercise you will use the features you learned on 8×8 patches sampled from images from the STL-10 dataset in the earlier exercise on linear decoders for classifying images from a reduced STL-10 dataset applying convolution and pooling. The reduced STL-10 dataset comprises 64×64 images from 4 classes (airplane, car, cat, dog).
这次作业依赖上一次“linear decoders”作业的代码,使用的数据是 STL-10 的一个子集,用来识别四种图像:飞机、汽车、猫和狗。
代码地址,由于 GIthub 有文件大小限制,所以这次没有上传数据文件。
Pooling 的代码比较简单,所以这里把计算卷积的代码详细注释后贴出来:
cnnConvolve.m
运行结果(识别的正确率):
- 使用 average pooling:

- 使用 max pooling: