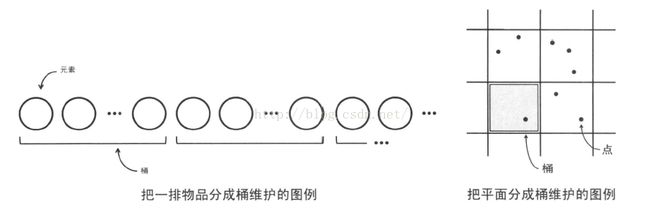
分桶法和平方分割
分桶法(bucketmethod)是把一排物品或者平面分成桶,每个桶分别维护自己内部的信息,以达到高效计算的目的的方法。
其中,平方分割(sqrtdecomposition)是把排成一排的n个元素每根号n个分在一个桶内进行维护的方法的统称。这样的分割方法可以使对区间的操作的复杂度降至O(根号n)。
和线段树一样,根据维护的数据不同,平方分割可以支持很多不同的操作。接下来,和线段树一样,我们以RMQ为例对平方分割进行详解。
1. 基于平方分割的RMQ
给定一个数列a1,a2,…,an,目标是在O(根号n)复杂度内实现两个功能
*给定s,t,求as,as+1,…,at的最小值
*给定t, x,把ai的值变为x。
2.基于平方分割RMQ的预处理
令b=floor(根号n),把a中的元素每b分成一个桶,并且计算出每个桶内的最小值。
3.基于平方分割的RMQ的查询
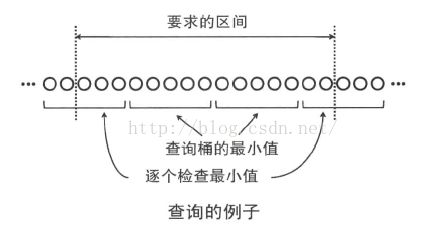
如下图所示,查询
*如果桶完全包含在区间内,则查询桶的最小值
*如果元素所在的桶不完全被区间包含,则逐个检查最小值
他们的最小值就是区间的最小值了。
4.基于平方分割的RMQ的值的更新
在更新元素的值时,需要更新该元素所在的桶的最小值。这时只要遍历一遍桶内的元素就可以了。
5.平方分割和线段树
因此,在平方分割中,对于任意区间,完全包含于其中的桶的数量和剩余元素的数量都是O(根号n),所以可以在O(根号n)时间内完成各种操作。
在上面的RMQ的例题中,线段树进行各种操作的复杂度是O(logn),比平方分割更快一些。一般地,如果线段树和平方分割都能实现某个功能,多数情况下线段树会比平方分割快。但是,因为平方分割在实现上比线段树简单,所以如果运行时间限制不是太紧时,也可以考虑使用平方分割。除此之外,也有一些功能是线段树无法高效维护但是平方分割却可以做到的。