poj 1556 The Doors（最短路+计算几何）
|
The Doors
Description
You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length.
Input
The input data for the illustrated chamber would appear as follows.
2 4 2 7 8 9 7 3 4.5 6 7 The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1. Output
The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.
Sample Input 1 5 4 6 7 8 2 4 2 7 8 9 7 3 4.5 6 7 -1 Sample Output 10.00 10.06 Source
Mid-Central USA 1996
|
[Submit] [Go Back] [Status] [Discuss]
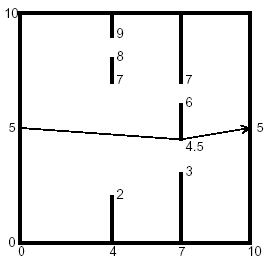
题目大意：在一个纵坐标为0-10，横坐标也为0-10的空间中有不超过18道竖立的墙（垂直于X轴），每道墙上两道门，求一条从（0，5）到（10，5）的最短路径长度。
题解：最短路径必定经过墙上门的端点。所有预处理出所有可以直接相连（即中间没有墙阻挡）的两个端点的直线距离，然后用FLOYED求最短路即可。判断有没有墙阻挡时，就是判段两个端点连成的线段，与他们所属墙之间的所有墙上的表示门的线段（有两个门，只要与其中一个相交即可）是否相交。
判断相交用跨立实验。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n,cnt,tot,vis[20];
double dis[100][100];
struct point
{
double x,y;
int pos;
point operator -(const point &a)
{
point t; t.x=x-a.x; t.y=y-a.y;
return t;
}
}p[100];
struct vector
{
double x,y;
vector operator =(const point &a)
{
this->x=a.x; this->y=a.y;
return *this;
}
double operator *(const vector &a)
{
return x*a.y-y*a.x;
}
}len[20][4];
double calc(int x,int y)
{
return sqrt((p[x].x-p[y].x)*(p[x].x-p[y].x)+(p[x].y-p[y].y)*(p[x].y-p[y].y));
}
bool pd(int t,int k,int i,int j)
{
vector t1; t1=p[j]-p[i];
for (int l=t;l<=k;l++)
{
bool f=false;
for (int h=1;h<=2;h++)
{
int t=(l-1)*4+1+(h-1)*2;
vector a,b,t2,c,d;
a=p[t+1]-p[i]; b=p[t+2]-p[i];
t2=p[t+2]-p[t+1];
c=p[i]-p[t+1]; d=p[j]-p[t+1];
double k1=(a*t1)*(t1*b);
double k2=(c*t2)*(t2*d);
if (k1>=0&&k2>=0) f=true;
}
if (f==false) return false;
}
return true;
}
int main()
{
while (scanf("%d",&n)!=EOF)
{
if (n==-1) break;
tot=0;
tot++; p[tot].x=0; p[tot].y=5; p[tot].pos=0;
for (int i=1;i<=n;i++)
{
double x,y,z,k,a; point t1,t2,t3,t4;
scanf("%lf%lf%lf%lf%lf",&a,&x,&y,&z,&k);
tot++; p[tot].x=a; p[tot].y=x; p[tot].pos=i; t1=p[tot];
tot++; p[tot].x=a; p[tot].y=y; p[tot].pos=i; t2=p[tot];
tot++; p[tot].x=a; p[tot].y=z; p[tot].pos=i; t3=p[tot];
tot++; p[tot].x=a; p[tot].y=k; p[tot].pos=i; t4=p[tot];
len[i][1]=t2-t1; cnt++; len[i][2]=t4-t3;
}
tot++; p[tot].x=10; p[tot].y=5; p[tot].pos=n+1;
for (int i=1;i<=tot-1;i++)
for (int j=i+1;j<=tot;j++)
{
dis[i][j]=dis[j][i]=dis[i][i]=dis[j][j]=1000000000;
if (pd(p[i].pos+1,p[j].pos-1,i,j)&&p[i].pos!=p[j].pos) dis[i][j]=dis[j][i]=calc(i,j);
}
for (int k=1;k<=tot;k++)
for (int i=1;i<=tot;i++)
for (int j=1;j<=tot;j++)
if (k!=i&&i!=j&&j!=k)
if (dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=dis[i][k]+dis[k][j];
printf("%0.2lf\n",dis[1][tot]);
}
}