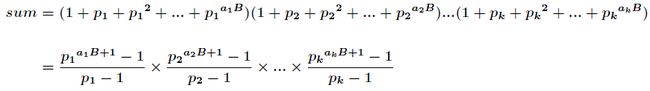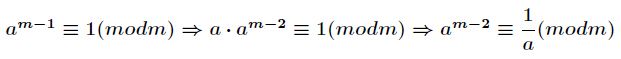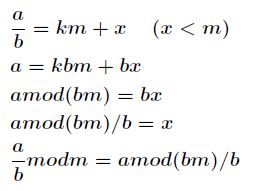poj1845 逆元,快速模幂
题目大意:
给定两个正整数![]() 和
和![]() ,求
,求![]() 的所有因子和对9901取余后的值。
的所有因子和对9901取余后的值。
分析:
很容易知道,先把![]() 分解得到
分解得到![]() ,那么得到
,那么得到![]() ,那么
,那么![]()
的所有因子和的表达式如下
因为要取模且存在除法,所以要用到逆元。
对于正整数![]() 和
和![]() ,如果有
,如果有![]() ,那么把这个同余方程中
,那么把这个同余方程中![]() 的最小正整数解叫做
的最小正整数解叫做![]() 模
模![]() 的逆元。
的逆元。
逆元一般用扩展欧几里得算法来求得,如果![]() 为素数,那么还可以根据费马小定理得到逆元为
为素数,那么还可以根据费马小定理得到逆元为![]() 。
。
推导过程如下
求现在来看一个逆元最常见问题,求如下表达式的值(已知![]() )
)
当然这个经典的问题有很多方法,最常见的就是扩展欧几里得,如果![]() 是素数,还可以用费马小定理。
是素数,还可以用费马小定理。
但是你会发现费马小定理和扩展欧几里得算法求逆元是有局限性的,它们都会要求![]() 与
与![]() 互素。实际上我们还有一
互素。实际上我们还有一
种通用的求逆元方法,适合所有情况。公式如下
现在我们来证明它,已知![]() ,证明步骤如下
,证明步骤如下
等比数列求和公式,用如下公式即可
因为![]() 可能会很大,超过int范围,所以在快速幂时要二分乘法。
可能会很大,超过int范围,所以在快速幂时要二分乘法。
接下来就是代码了:(一定要讲乘法二分,还有取模后一定要加模)
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <map>
#include <set>
#include <iomanip>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define maxn 10005
#define MOD 1000000007
#define mem(a , b) memset(a , b , sizeof(a))
#define LL long long
#define ULL long long
const long long INF=0x3fffffff;
bool prime[maxn];
int p[maxn];
void is_prime()
{
mem(prime , true);
int id = 0;
prime[0] = prime[1] = false;
for(int i = 2 ; i < maxn ; i ++)
{
if(prime[i])
{
p[id++] = i;
int j = 2 * i;
while(j <= maxn) prime[j] = false , j += i;
}
}
}
LL mulit(LL a , LL b , LL mod)
{
a %= mod;
b %= mod;
LL res = 0;
while(b)
{
if(b & 1)
{
res = (res + a) % mod;
}
b >>= 1;
a = (a + a) % mod;
}
return res % mod;
}
LL quick_mod(LL a , LL b , LL mod)
{
LL res = 1;
while(b)
{
if(b & 1)
{
res = mulit(res , a , mod);
}
a = mulit(a , a , mod);
b >>= 1;
}
return res;
}
//ofstream ofile;
int main()
{
LL a , b;
is_prime();
while(scanf("%lld %lld",&a , &b) != EOF )
{
LL ans = 1;
for(int i = 0 ; p[i] * p[i] <= a ; i++)
{
if(a % p[i] == 0)
{
int num = 0;
while(a % p[i] == 0)
{
num ++;
a /= p[i];
}
ans *= (quick_mod(p[i] , num * b+1 , 9901 *(p[i]-1) ) + (9901 *(p[i]-1))- 1) / (p[i] - 1);
ans %= 9901;
}
}
if(a > 1)
{
ans *= (quick_mod(a , b+1 , 9901 *(a-1) ) + 9901 *(a-1) - 1) / (a - 1);
ans %= 9901;
}
cout << ans << endl;
}
return 0;
}