C++ 图的几种表示方法解析

最近学习了一下图论，对于图的表示方法自然也有所接触，在题目数据范围较小的时候，我们可以使用邻接矩阵，

在图的邻接矩阵表示法中：

    ① 用邻接矩阵表示顶点间的相邻关系

　 ② 用一个顺序表来存储顶点信息

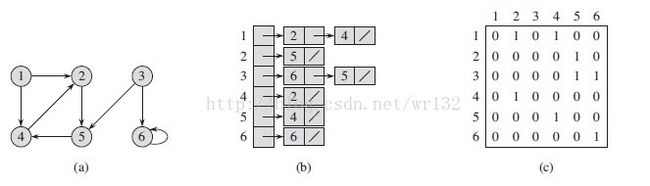
设G=(V，E)是具有n个顶点的图，则G的邻接矩阵是具有如下性质的n阶方阵：

【例】下图中无向图G 5 和有向图G 6 的邻接矩阵分别为A1和A2 。

但是，当数据比较分散的时候，例如稀疏图，用邻接矩阵会造成很大的内存浪费，所以就出现了邻接表的表示方式

邻接表(Adjacency List)是图的一种顺序存储与链式存储结合的存储方法，类似于树的孩子链表表示法。由于它只考虑非零元素,因而节省了零元素所占的存储空间。它对于无向图和有向图都适用。

邻接表示法就是对于图G中的每个顶点放到一个数组中，数组的每个元素存放一个结点并指向一个单链表的指针。链表中存储着与该顶点相邻接的顶点所在的数组元素的下标。

建表的几种方式：

1.数据结构树上给出的，通过链表的方式，理解简单，但效率不高

typedef struct Node
{
    int dest;                    //邻接边的弧头结点序号
    int weight;                    //权值信息
    struct Node *next;            //指向下一条邻接边
}Edge;                            //单链表结点的结构体

typedef struct
{
    DataType data;                //结点的一些数据，比如名字
    int sorce;                    //邻接边的弧尾结点序号
    Edge *adj;                    //邻接边头指针
}AdjHeight;                        //数组的数据元素类型的结构体

typedef struct
{
    AdjHeight a[MaxVertices];    //邻接表数组
    int numOfVerts;                //结点个数
    int numOfEdges;                //边个数
}AdjGraph;                        //邻接表结构体

2.通过数组方式（更加简洁高效的邻接表制法）

<span style="font-size:24px;">typedef struct
{
    int to;
    int w;
    int next;
}Edge;
Edge e[MAX];
int pre[MAX];

//初始化
memset(pre,-1,sizeof(pre));

//输入
scanf("%d %d %d",&from,&to,&w1);
e[i].to = to; e[i].w = w1; e[i].next = pre[from]; pre[from] = i;
i++;</span>

在查找某个节点的邻接点的时候可以这样写

/*now为弧尾结点序号，i为now所发出的边序号，adj为弧头结点序号，w为now-->adj这条边的权值*/
for(i = pre[now]; i != -1; i = edge[i].next)
{
     int adj = edge[i].to;
     int w = edge[i].w;
     //do something...
}

下面说明一下建标的原理，结构体内的信息：1.to 一条有向线段的终点 2.w 这条边的权值 3.next 这条边所连接的下一条有相同起点的边，pre[i]（也常写成head[i]），存储以节点i为出发点，并且直接与节点i相连的边。

在输入加边的时候，相信大家主要是纠结这两句话的意思

e[i].next = pre[from];          pre[from] = i；

首先，让我们理清一下建表的过程，首先，插入一条边，这条边以from为起点，而pre[from]中存放的则是以from为起点并且直接与点from相连的那条边，于是

e[i].next = pre[from]; 就可以做到 将那条边连同其后的所有边都从点from上拔下来，插到边e[i]的后面，而pre[from]=i；则做到了将这条新的，更长的，以e[i]为首的边插到点from上，从而完成了一次边的更新，这样在访问的时候，就可以通过e[i].next找到所有以from为起点的边，而每条边的终点to则就是我们要找的与from相邻的点