常用八大排序算法

常用八大排序算法

排序分为内部排序和外部排序。内部排序在内存中进行，外部排序使用内存和外存实现。
本文介绍的八种排序算法属于内部排序，使用java语言实现。

1.冒泡排序(BubbleSort)

1.1 排序思想：
冒泡排序，一组无序的数，对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。
1.2 冒泡排序图示:

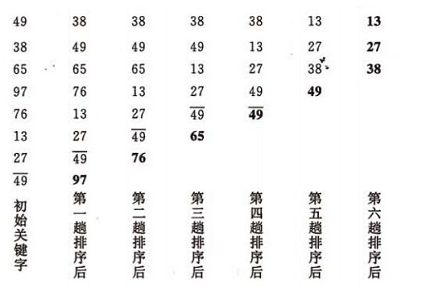
1.3 算法java代码实现:

public void bubbleSort()
    {
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<n-i;j++)
            {
                if(a[j]>a[j+1])
                {
                    swap(j,j+1);
                }
            }
        }
    }

1.4 时间复杂度：O(n^2)
2.选择排序(SelectSort)

2.1 排序思想:
选择排序，一组无序的数，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，完成从小到大（或者从大到小）排序。
2.2 选择排序图示:

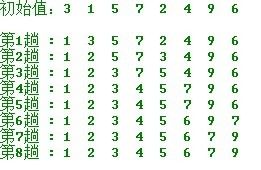
2.3 算法java代码实现：

public void selectSort()
    {
        for(int i=0;i<n;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                if(a[i]<a[j])
                {
                    swap(i,j);
                }
            }
        }
    }

2.4 时间复杂度：O(n^2)
3.插入排序(InsertSort)

3.1 排序思想:
插入排序，将序列的第1个元素看作一个有序的子序列，然后向该子序列中逐个插入剩余的元素直到序列完全有序。
3.2 插入排序图示：

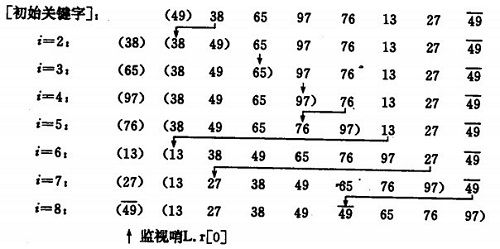
3.3 算法java代码实现：

public void insertionSort()
    {
        int i,j;
        for(i=0;i<n;i++)
        {
            long temp=a[i];
            j=i;
            while(j>0&&a[j-1]>=temp)
            {
                a[j]=a[j-1];
                --j;
            }
            a[j]=temp;
        }
    }

3.4 时间复杂度：O(n^2)
4.归并排序(MergeSort)

4.1 排序思想：
归并排序,将一个无序序列反复平分，设定只有一个数据项的子序列是有序的（基值条件）,然后在依次归并子序列，生成一个有序的原序列。
4.2 归并排序图示:

4.3 算法java代码实现：

private void merge(long[] workSpace,int low,int high,int upper){
        int j=0;
        int lower=low;
        int mid=high-1;
        int n=upper-lower+1;
        while(low<=mid&&high<=upper){
            if(theArray[low]<theArray[high])
                workSpace[j++]=theArray[low++];
            else {
                workSpace[j++]=theArray[high++];
            }
        }
        while(low<=mid)
            workSpace[j++]=theArray[low++];
        while(high<=upper)
            workSpace[j++]=theArray[high++];

        for(j=0;j<n;j++)
            theArray[lower+j]=workSpace[j];

    }

4.4 时间复杂度：O(N*logN)
5.希尔排序(ShellSort)

5.1 排序思想:
希尔排序，基于插入排序，加大插入排序中元素之间的间隔，并在这些有间隔的元素之间进行插入排序，从而使数据项可以大幅度跨动，一趟排序完成后，减小间隔（间隔最小是1）再排序，依次进行下去，。
5.2 希尔排序图示:

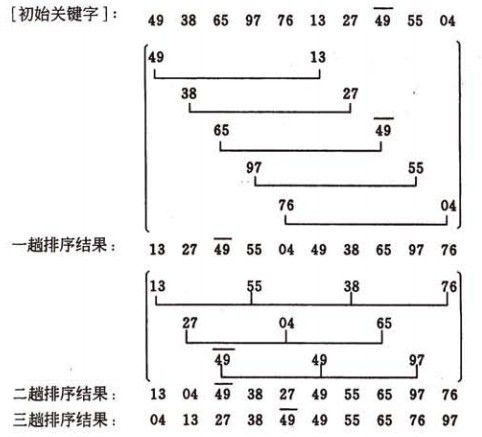
5.3 算法java代码实现：

public void shellSort(){
        int h=1;
        int inner,outer;
        long temp;
        while(h<=n/3)
            h=h*3+1;
        while(h>0){
            for(outer=h;outer<n;outer++){
                temp=theArray[outer];
                inner=outer;
                while(inner>h-1&&theArray[inner-h]>=temp){
                    theArray[inner]=theArray[inner-h];
                    inner=inner-h;
                }
                theArray[inner]=temp;
            }
            h=(h-1)/3;
        }
    }

5.4 时间复杂度：没有确定的，O（N^(x/y))
6.快速排序(QuickSort)
6.1 排序思想：
快速排序，首先，选择序列中一个基准元素（三数据项取中法）；然后，通过一趟排序把无序的序列分割成两部分，其中一部分序列的元素值比基准元素值小，另一部分序列的 元素值比基准值大，并且基准元素在其排好序后的正确位置；接着，再对这两部分序列用同样的方法进行排序，依次进行下去；最后，整个序列有序。
6.2 快速排序图示：

6.3 算法java代码实现:

public void quickSort(){
        recQuickSort(0,n-1);
    }
    public void recQuickSort(int left,int right){
        int size=right-left+1;
        if(size<=3)
            manualSort(left,right);
        else {
            long median=median3(left,right);
            int partition=partitionIt(left,right,median);
            recQuickSort(left,partition-1);
            recQuickSort(partition+1,right);
        }
    }
    public long median3(int left,int right){
        int center=(left+right)/2;
        if(theArray[left]>theArray[center])
            swap(left,center);
        if(theArray[left]>theArray[right])
            swap(left,right);
        if(theArray[center]>theArray[right])
            swap(center,right);
        swap(center,right);
        return theArray[right];
    }
    public void swap(int dex1,int dex2){
        long t=theArray[dex1];
        theArray[dex1]=theArray[dex2];
        theArray[dex2]=t;
    }
    public int partitionIt(int left,int right,long pivon){
        int leftptr=left;
        int rightptr=right;
        while(true){
            while(theArray[++leftptr]<pivon)
                ;
            while(theArray[--rightptr]>pivon)
                ;
            if(leftptr>=rightptr)
                break;
            else {
                swap(leftptr, rightptr);
            }
        }
        swap(leftptr, right);
        return leftptr;
    }
    public void manualSort(int left,int right){
        int size=right-left+1;
        if(size<=1)
            return;
        else if(size==2){
            if(theArray[left]>theArray[right])
                swap(left, right);
            return;
        }else{
            if(theArray[left]>theArray[right-1])
                swap(left, right-1);
            if(theArray[left]>theArray[right])
                swap(left, right);
            if(theArray[right-1]>theArray[right])
                swap(right-1, right);
        }
    }

时间复杂度：O(N*logN)
7.基数排序(RadixSort)
7.1 排序思想：
十进制数为例:

7.2 基数排序图示：

7.3 算法java代码实现

class RadixSort {
    // 获取x这个数的d位数上的数字
    // 比如获取123的1位数，结果返回3
    public int getDigit(int x, int d) {
        int a[] = {
                1, 1, 10, 100
        }; // 本实例中的最大数是百位数，所以只要到100就可以了
        return ((x / a[d]) % 10);
    }

    public void radixSort(int[] list, int begin, int end, int digit) {
        final int radix = 10; // 基数
        int i = 0, j = 0;
        int[] count = new int[radix]; // 存放各个桶的数据统计个数
        int[] bucket = new int[end - begin + 1]; 
        // 按照从低位到高位的顺序执行排序过程
        for (int d = 1; d <= digit; d++) {
            // 置空各个桶的数据统计
            for (i = 0; i < radix; i++) {
                count[i] = 0;
            }
            // 统计各个桶将要装入的数据个数
            for (i = begin; i <= end; i++) {
                j = getDigit(list[i], d);
                count[j]++;
            }
            // count[i]表示第i个桶的右边界索引
            for (i = 1; i < radix; i++) {
                count[i] = count[i] + count[i - 1];
            }

            // 将数据依次装入桶中
            // 这里要从右向左扫描，保证排序稳定性
            for (i = end; i >= begin; i--) {
                j = getDigit(list[i], d); // 求出关键码的第k位的数字， 例如：576的第3位是5
                bucket[count[j] - 1] = list[i]; // 放入对应的桶中，count[j]-1是第j个桶的右边界索引
                count[j]--; // 对应桶的装入数据索引减一
            }
            // 将已分配好的桶中数据再倒出来，此时已是对应当前位数有序的表
            for (i = begin, j = 0; i <= end; i++, j++) {
                list[i] = bucket[j];
            }
        }
    }

    public int[] sort(int[] list) {
        radixSort(list, 0, list.length - 1, 3);
        return list;
    }
}

7.4 时间复杂度：O(N*logN)
8.堆排序(HeapSort)
8.1 排序思想:
堆(一种二叉树)排序，在堆中插入全部无序的数据项，然后重复移除，就可以按序移除数据项。
堆的特点：
1.完全二叉树
2.常用数组实现
3.每个节点的关键字都大于其子节点的关键字
8.2 堆排序图示：

8.3 算法java代码实现

class Node
   {
   private int iData;            
   public Node(int key)          
      { iData = key; }
   public int getKey()
      { return iData; }
   }  
class Heap
   {
   private Node[] heapArray;
   private int maxSize;           
   private int currentSize;       
   public Heap(int mx)           
      {
      maxSize = mx;
      currentSize = 0;
      heapArray = new Node[maxSize];
      }
   public Node remove()           
      {                          
      Node root = heapArray[0];
      heapArray[0] = heapArray[--currentSize];
      trickleDown(0);
      return root;
      }  
   public void trickleDown(int index)
      {
      int largerChild;
      Node top = heapArray[index];      
      while(index < currentSize/2)        
         {
         int leftChild = 2*index+1;
         int rightChild = leftChild+1;

         if(rightChild < currentSize &&   
                             heapArray[leftChild].getKey() <
                             heapArray[rightChild].getKey())
            largerChild = rightChild;
         else
            largerChild = leftChild;

         if(top.getKey() >= heapArray[largerChild].getKey())
            break;                                        
         heapArray[index] = heapArray[largerChild];
         index = largerChild;             
         }  
      heapArray[index] = top;           
      }      
   public void insertAt(int index, Node newNode)
      { heapArray[index] = newNode; }
   public void incrementSize()
      { currentSize++; }
   }  

8.4 时间复杂度：O(N*logN)

总结
1.各种排序算法时间、空间复杂度及稳定性

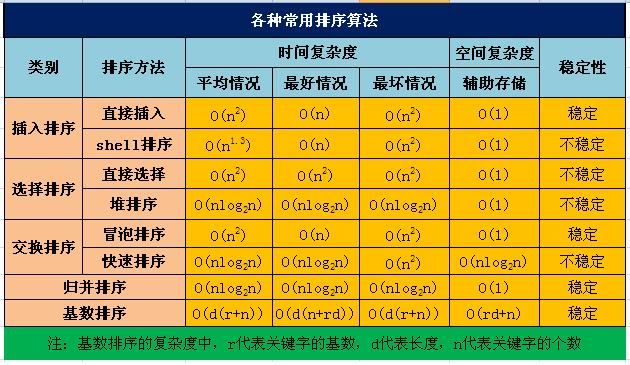
2.各种排序算法时间复杂度比较：
当n特别大时，则应该使用时间复杂度为O(NlogN)的排序方法：快速排序，堆排序，归并排序。

备注
推荐一本数据结构与算法的书：Data Structures & Algorithms in Java（Robert Lafore）,中文版本叫做:Java数据结构和算法（第二版）

本文的部分排序示意图参照了：http://blog.csdn.net/hguisu/article/details/7776068