时间序列 R 09 ARIMA

1.1 稳定性与差分

1.1.1 稳定性 stationarity

稳定性是指时间序列的属性不在随时间变化。因此有趋势和季节性的时间序列不是稳定的序列。但是有一些具有周期性cyclic的时间序列因为其周期时间不一定，所以也是稳定性序列。

1.1.2 差分 Differencing

下图a，b分别是道琼斯指数与道琼斯指数每天的变化量

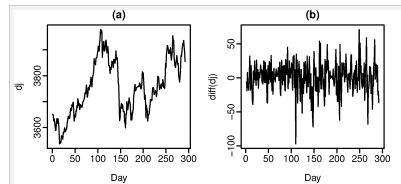
下图是两幅图的ACF

第二幅中仅有一个是稍大于95%线，而且Ljung-Box Q∗的p-value值为0.153 (for h=10h=10)，可见b是稳定的，而显然a是不稳定的。这种计算连续值的differences的方法就叫做differencing（差分）。

1.1.3 随机游动 random walk

前面写过，http://blog.csdn.net/bea_tree/article/details/51173337#t3。
这是一种非稳定序列，其预测方法为naive方法。即预测值为最后一次观察值。
另外与之相近的一种模式如下式：

yt−yt−1=c+etoryt=c+yt−1+et:.

这种模式有一个常数c，因此有不断增长或者降低的趋势，期预测方法为drift法。

1.1.4 二阶差分

在差分的基础之上在进行一次差分为二次差分：

y′′t=y′t−y′t−1=(yt−yt−1)−(yt−1−yt−2)=yt−2yt−1+yt−2.

实际中一般很少需要二阶以上差分，一阶差分只有t-1个值，二阶差分只有t-2个值。

1.1.5 lag-m差分Seasonal differences

在对季节性数据进行查分时往往不是进行相邻数据的差分，而是用下式进行差分：

y′t=yt−yt−m其中 m= number of seasons.

这叫做m滞后差分，也叫Seasonal differences 。
如果得到的差分结果是白噪声，其预测方法用naive seasonal 方法，直接以最后一个周期为预测值
下图是在进行log转换后进行了一次seasonal差分，发现可能还不稳定，然后又进行了一次一阶差分

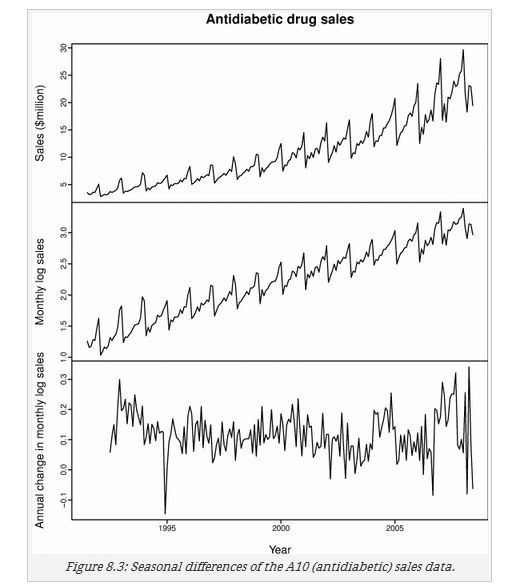
这样两次差分的方程为：

y′′t=y′t−y′t−1=(yt−yt−m)−(yt−1−yt−m−1)=yt−yt−1−yt−m+yt−m−1.

可见这两次差分谁在前面都是一样的结果，但是如果周期性比较好，建议先进行周期性差分，这样可能只进行周期性差分就可以得到一个稳定序列，但是如果只进行一阶差分一般得到的结果还是周期性的结果。

1.1.6 单位根检验 Unit root tests

关于什么是单位根，http://blog.sina.com.cn/s/blog_6d0417a501017jrq.html。
这里我们只要知道单位根检验就看时间序列是否稳定的检验就可以了。
文中介绍了两种方法Augmented Dickey-Fuller (ADF) test和Kwiatkowski-Phillips-Schmidt-Shin (KPSS)
ADF的回归方程为：

y′t=ϕyt−1+β1y′t−1+β2y′t−2+⋯+βky′t−k,

如果原算式 yt 是不稳定的， ϕ^ 将是接近于0的，如果是稳定的将是小于0的。
R中的命令是

adf.test(x, alternative = "stationary")

其零假设为原序列是不稳定的，所以得到的P-value越小越稳定
而在KPSS中预期相反，得到的值越大越稳定
KPSS的Rcode是

kpss.test(x)

另外，R语言中ndiffs()是一个很有用函数，可以判断一个序列需要的差分数。nsdiffs()是判断一个季节性序列所需要的差分数，一般季节性差分可能需要与lag-1差分混合使用，下面是使季节性数据稳定的栗子：

ns <- nsdiffs(x)
if(ns > 0) {
  xstar <- diff(x,lag=frequency(x),differences=ns)
} else {
  xstar <- x
}
nd <- ndiffs(xstar)
if(nd > 0) {
  xstar <- diff(xstar,differences=nd)
}

结果储存在xstar中。

1.2 backshift notation

backshift的定义如下：

Byt=yt−1.

并定义:

B(Byt)=B2yt=yt−2.

一阶差分用B表达

y′t=yt−yt−1=yt−Byt=(1−B)yt

二阶差分

y′′t=yt−2yt−1+yt−2=(1−2B+B2)yt=(1−B)2yt.

d阶

(1−B)dyt.

在多种差分合并的时候，这种标记形式非常方便：

(1−B)(1−Bm)yt=(1−B−Bm+Bm+1)yt=yt−yt−1−yt−m+yt−m−1,

1.3 自回归模型 AR(p)

自回归模型是指形如下式的模型：

yt=c+ϕ1yt−1+ϕ2yt−2+⋯+ϕpyt−p+et,

yt 只与之后的 yt−1 等值相关。
下面两幅图是p=1 和等于2时的图像

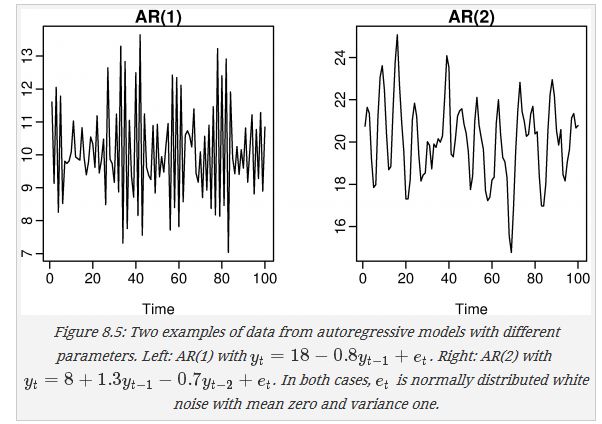
对于AR（1）
当ϕ1=0，yt 是白噪声
当ϕ1=1且c=0, yt是 random walk.
当ϕ1=1且c≠0, yt是 random walk with drift（有漂移项）
当ϕ1<0, yt常会在正负值之间摆动.
我们常常用以下约束来将序列限制在稳定序列中.

对于 AR(1) model: −1<ϕ1<1
对于AR(2) model: −1<ϕ2<1, ϕ1+ϕ2<1, ϕ2−ϕ1<1.
当P大于3时限制条件更加复杂，R中的函数会帮我们弄好限制.

1.4 Moving average models， ＭＡ

ＭＡ模型只与前q期的误差有关

yt=c+et+θ1et−1+θ2et−2+⋯+θqet−q,

以下是q=1,2的情景

对于AR（p）可以写成MA（ ∞ ）的形式，比如

yt=ϕ1yt−1+et=ϕ1(ϕ1yt−2+et−1)+et=ϕ21yt−2+ϕ1et−1+et=ϕ31yt−3+ϕ21et−2+ϕ1et−1+etetc.

当 ϕ 在-1到1之间时，它的指数逐渐增加，其值逐渐变小,得到下式

yt=et+ϕ1et−1+ϕ21et−2+ϕ31et−3+⋯,

同样我们在一定的限制时也可以将MA（p）可以写成AR（ ∞ ）的形式，其限制条件为
For an MA(1) model: −1<θ1<1.
For an MA(2) model: −1<θ2<1, θ2+θ1>−1, θ1−θ2<1

1.5 Non-seasonal ARIMA models

1.5.1 AutoRegressive Integrated Moving Average model

arima是将ar和ma联合起来的模型

y′t=c+ϕ1y′t−1+⋯+ϕpy′t−p+θ1et−1+⋯+θqet−q+et,

此模型成为 ARIMA(p,d,q) model，其中d的意义为变为平稳序列的差分阶数，使用B形式表示为：

(1−ϕ1B−⋯−ϕpBp)↑AR(p)(1−B)dyt↑d differences=c+(1+θ1B+⋯+θqBq)et↑MA(q)

pdq的选取是一件很复杂的事情，幸好万能的R可使用 auto.arima()来自动计算pdq。
如果套用上面的arima的定义我们已经见过以下形式：

下例是利用auto.arima求解的

> fit <- auto.arima(usconsumption[,1],seasonal=FALSE) ARIMA(0,0,3) with non-zero mean Coefficients: ma1 ma2 ma3 intercept 0.2542 0.2260 0.2695 0.7562 s.e. 0.0767 0.0779 0.0692 0.0844 sigma^2 estimated as 0.3856: log likelihood=-154.73 AIC=319.46 AICc=319.84 BIC=334.96

得到的结果为

yt=0.756+et+0.254et−1+0.226et−2+0.269et−3,

这是预测结果：

plot(forecast(fit,h=10),include=80)

1.5.2 理解Arima

Arima中常数c和阶数d有着重要的意义

其中d代表差分阶数，d越大其预测的方差将会变化（变大）的越迅速。
上面的栗子中c不等于0，d等于0，所以其预测值最后倾向于收敛于数据的平均值。
另外在cyclic的数据中，p的值是重要的。一般的cyclic的数据中p的值会大于2，如果p=2时有cyclic，此时应满足 ϕ21+4ϕ2<0 此时的cyclic的周期是

2πarc cos(−ϕ1(1−ϕ2)/(4ϕ2)).

1.5.3 ACF，PACF

有时候可以借助ACF和pacf来判断Arima中的pdq的值
acf是判断自相关的函数，但是有时候不相关的两个数也会有很大的ACF比如，如果a与b相关，a与c相关，但是可能b与c之间并不包含来预测新值的有效信息时也有很大的相关系数
这时可以用pacf（partial autocorrelations fraction），他的系数由ar等式确定

αk=kth partial autocorrelation coefficient=the estimate of ϕk in the autoregression modelyt=c+ϕ1yt−1+ϕ2yt−2+⋯+ϕkyt−k+et.

其95%临界值也是 ±1.96/T−−√
下图是上例的ACF pacf图像

对于ARIMA(p,d,0) or ARIMA(0,d,q) 两种模式可以由ACF和PACf图判断参数，方法如下：
ARIMA(p,d,0)
1. ACF 呈指数衰减或周期震荡;
2. 在 PACF上有一个突出的lag p, 但是p之后不再有突出的lag.
ARIMA(0,d,q)
1. PACF 呈指数衰减或周期震荡;
2. 在 ACF上有一个突出的lag p, 但是p之后不再有突出的lag.
文中说，因为在lag3之后ACF没有突出的lag，PACF程指数衰减（decay exponentially）（可能是再去除偶尔突出的lag之后看到的粗略的结果），所以是Arima（0,0,3）模式

1.6 参数确定与模型选择

1.6.1 参数确定

模型选择之后，需要确定 c，ϕ1,…,ϕp 等值，R中使用的是最大似然估计（maximum likehood estimator MLE），也可以使用最小二乘法（ least squares estimates）获得，很多时候二者是相同的。

1.6.2 模型选择

这里主要指的是pdq的判断，使用的方法还是ＡＩＣ，BIC，AICc，以前写过
http://blog.csdn.net/bea_tree/article/details/51197704#t21
公式分别如下：

AIC=−2log(L)+2(p+q+k+1),AICc=AIC+2(p+q+k+1)(p+q+k+2)T−p−q−k−2.BIC=AIC+(log(T)−2)(p+q+k+1).

文中说倾向于AICc。

1.7 ARIMA modelling in R

1.7.1 auto.arima()

该函数使用Hyndman and Khandakar algorithm
R中的求解步骤
1. 利用KPSS求解差分阶数d
2. 利用AICc ，使用逐步搜索（stepwise search）的方法求解差分之后的p，q
逐步搜索（stepwise search）的方法如下：

(a) 从下列四个模型中选取最佳模型:
ARIMA(2,d,2),
ARIMA(0,d,0),
ARIMA(1,d,0),
ARIMA(0,d,1).

如果d≥1将常数c设为0（不考虑常数项），d=0时正常计算c.

(b) 改变上面选择的模型:

• 将p，q改变±1;
• 添加或去掉常数c
• 将上面几步得到的最好的模型留下

(c) 重复(b) 直到 AICc 无法更小.

1.7.2 建模流程

其中手动建模中的选择的模型可以多样，比如感觉（003）对可以试试（004），114 ，014， 104 113 013 103 等模式

1.7.3 理解常数

non-seasonal Arima可以写成下式

(1−ϕ1B−⋯−ϕpBp)(1−B)dyt=c+(1+θ1B+⋯+θqBq)et

也可写成下式

(1−ϕ1B−⋯−ϕpBp)(1−B)d(yt−μtd/d!)=(1+θ1B+⋯+θqBq)et,

R中使用的是后者
其中 c=μ(1−ϕ1−⋯−ϕp) , μ 是 (1−B)dyt 的均值。
当d=0时 μ 是yt的均值
当不稳定序列包含常数时，会在预测中产生次数为d的多项式趋势
- arima()
默认时若d>0,c=μ=0 d=0时给μ一个估计值. μ是输出的截距“intercept”，接近时间序列的均值, 但当 p+q>0时通常不认为均值能是MIE（最大似然估计）最大. 其参数.mean 默认为truth，且当d=0是才有效. S当设为FALSE强制设μ=0.

• Arima()
  除了有arima中的.mean 相同的功能外，还有.drift这一参数，它允许d=1时μ≠0. d>1, 时不允许有常数 ，d=1时的μ就是输出的“drift” .

还有一个参数constant，若设置为FALSE,mean和.drift 都会设为 FALSE. 像是总开关的样子

• auto.arima()
  默认时，常数项自动取值使AIC最小，但是若d>1常数忽略. 如果allowdrift=FALSE常数项只有d=0时有效

1.8 预测

其得到预测结果的步骤如下
1. 展开得到的拟合表达式，写成 yt 左边的形式
2. 将公式里 t改为T+h
3. 代入预测值，未知的误差代入0，可以计算的误差用相应值代替。
对于h从1到我们需要的预测的值，代入重复以上3步。
预测区间的确定比较复杂，此处不讨论。可以看这本书。
预测时基于残差是正态分布且不相关进行的，所以应该时常检查ACF和残差分布图，以检查此假设是否正确

1.9 Seasonal ARIMA models

1.9.1 形式

以上都是讨论的非季节性的Arima，在含有季节性的时间序列使用Arima时，只是加入了一个seasonal的参数

以ARIMA(1,1,1)(1,1,1) 4 为例

添加的季节性数据只是简单的乘在了公式两边

1.9.2 ACF/PACF

查看ACF/PACF在seasonal时的表现形式
ARIMA(0,0,0)(0,0,1) 12
- ACF 中lag12会突出，但是其他不突出.
- PACF 在 lags 12, 24, 36, ….等成指数性衰减
同样ARIMA(0,0,0)(1,0,0) 12 :
- ACF 在 lags 12, 24, 36, ….等成指数性衰减
- PACF 中lag12会突出，但是其他不突出.

1.9.3 auto.arima()

教材中对同一个案例使用手动建模和auto.arima()建模
在使用auto.arima()时，可关闭加速运算的选项得到更好的结果，代码如下：

> auto.arima(euretail)
ARIMA(1,1,1)(0,1,1)[4]                    

Coefficients:
 ar1 ma1 sma1
 0.8828 -0.5208 -0.9704
s.e.  0.1424   0.1755   0.6792

sigma^2 estimated as 0.1411:  log likelihood=-30.19
AIC=68.37 AICc=69.11 BIC=76.68 --------------------------------------------------
> auto.arima(euretail, stepwise=FALSE, approximation=FALSE)
ARIMA(0,1,3)(0,1,1)[4]                    

Coefficients:
 ma1 ma2 ma3 sma1
 0.2625 0.3697 0.4194 -0.6615
s.e.  0.1239  0.1260  0.1296   0.1555

sigma^2 estimated as 0.1451:  log likelihood=-28.7
AIC=67.4   AICc=68.53   BIC=77.78

在另外一个例子中，作者首先手动确定了一个模型model1，Ljung-Box test（点击查看链接）未通过，接着使用自动求解，得到的模型model2 其Ljung-Box test也没有通过，根据手动建立的模型调整参数，自动求解之后得到的模型model3全部通过。
但是在后续的比较和筛选中，model2和model3的拟合情况都不如model1，所以最后选择了model1.
说明了
1. 不一定所有的测试都必须通过
2. 自动求解不一定给出最好的答案（一般都是接近于最好的答案）

1.10 ARIMA vs ETS

两种模型的参数比较